Symmetric Positive Semi-definite Riemannian Geometry with Application to Domain Adaptation

In this paper, we present new results on the Riemannian geometry of symmetric positive semi-definite (SPSD) matrices. First, based on an existing approximation of the geodesic path, we introduce approximations of the logarithmic and exponential maps. Second, we present a closed-form expression for Parallel Transport (PT). Third, we derive a canonical representation for a set of SPSD matrices. Based on these results, we propose an algorithm for Domain Adaptation (DA) and demonstrate its performance in two applications: fusion of hyper-spectral images and motion identification.

Spectral Discovery of Jointly Smooth Features for Multimodal Data

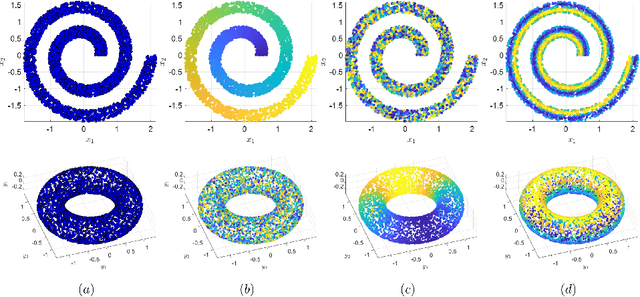
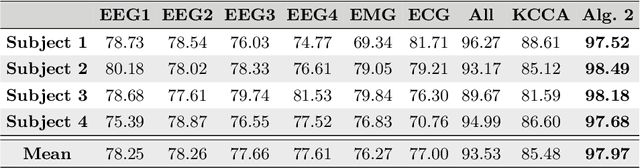
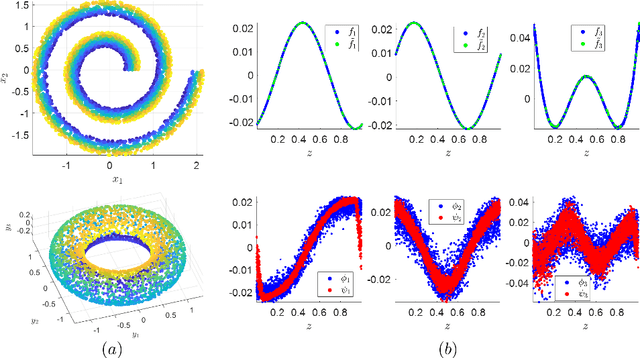
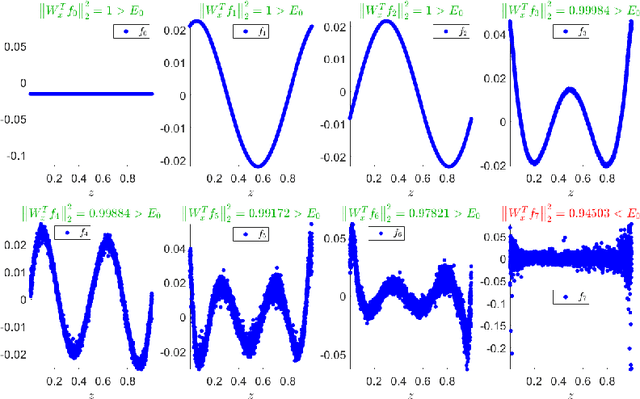
In this paper, we propose a spectral method for deriving functions that are jointly smooth on multiple observed manifolds. Our method is unsupervised and primarily consists of two steps. First, using kernels, we obtain a subspace spanning smooth functions on each manifold. Then, we apply a spectral method to the obtained subspaces and discover functions that are jointly smooth on all manifolds. We show analytically that our method is guaranteed to provide a set of orthogonal functions that are as jointly smooth as possible, ordered from the smoothest to the least smooth. In addition, we show that the proposed method can be efficiently extended to unseen data using the Nystr\"{o}m method. We demonstrate the proposed method on both simulated and real measured data and compare the results to nonlinear variants of the seminal Canonical Correlation Analysis (CCA). Particularly, we show superior results for sleep stage identification. In addition, we show how the proposed method can be leveraged for finding minimal realizations of parameter spaces of nonlinear dynamical systems.

Optimal Transport on the Manifold of SPD Matrices for Domain Adaptation

The problem of domain adaptation has become central in many applications from a broad range of fields. Recently, it was proposed to use Optimal Transport (OT) to solve it. In this paper, we model the difference between the two domains by a diffeomorphism and use the polar factorization theorem to claim that OT is indeed optimal for domain adaptation in a well-defined sense, up to a volume preserving map. We then focus on the manifold of Symmetric and Positive-Definite (SPD) matrices, whose structure provided a useful context in recent applications. We demonstrate the polar factorization theorem on this manifold. Due to the uniqueness of the weighted Riemannian mean, and by exploiting existing regularized OT algorithms, we formulate a simple algorithm that maps the source domain to the target domain. We test our algorithm on two Brain-Computer Interface (BCI) data sets and observe state of the art performance.

Local Canonical Correlation Analysis for Nonlinear Common Variables Discovery

In this paper, we address the problem of hidden common variables discovery from multimodal data sets of nonlinear high-dimensional observations. We present a metric based on local applications of canonical correlation analysis (CCA) and incorporate it in a kernel-based manifold learning technique.We show that this metric discovers the hidden common variables underlying the multimodal observations by estimating the Euclidean distance between them. Our approach can be viewed both as an extension of CCA to a nonlinear setting as well as an extension of manifold learning to multiple data sets. Experimental results show that our method indeed discovers the common variables underlying high-dimensional nonlinear observations without assuming prior rigid model assumptions.