Domain Adaptation for DoA Estimation in Multipath Channels with Interferences

We consider the problem of estimating the direction-of-arrival (DoA) of a desired source located in a known region of interest in the presence of interfering sources and multipath. We propose an approach that precedes the DoA estimation and relies on generating a set of reference steering vectors. The steering vectors' generative model is a free space model, which is beneficial for many DoA estimation algorithms. The set of reference steering vectors is then used to compute a function that maps the received signals from the adverse environment to a reference domain free from interfering sources and multipath. We show theoretically and empirically that the proposed map, which is analogous to domain adaption, improves DoA estimation by mitigating interference and multipath effects. Specifically, we demonstrate a substantial improvement in accuracy when the proposed approach is applied before three commonly used beamformers: the delay-and-sum (DS), the minimum variance distortionless response (MVDR), and the Multiple Signal Classification (MUSIC).

Riemannian Covariance Fitting for Direction-of-Arrival Estimation

Covariance fitting (CF) is a comprehensive approach for direction of arrival (DoA) estimation, consolidating many common solutions. Standard practice is to use Euclidean criteria for CF, disregarding the intrinsic Hermitian positive-definite (HPD) geometry of the spatial covariance matrices. We assert that this oversight leads to inherent limitations. In this paper, as a remedy, we present a comprehensive study of the use of various Riemannian metrics of HPD matrices in CF. We focus on the advantages of the Affine-Invariant (AI) and the Log-Euclidean (LE) Riemannian metrics. Consequently, we propose a new practical beamformer based on the LE metric and derive analytically its spatial characteristics, such as the beamwidth and sidelobe attenuation, under noisy conditions. Comparing these features to classical beamformers shows significant advantage. In addition, we demonstrate, both theoretically and experimentally, the LE beamformer's robustness in scenarios with small sample sizes and in the presence of noise, interference, and multipath channels.

The Expected Loss of Preconditioned Langevin Dynamics Reveals the Hessian Rank

Langevin dynamics (LD) is widely used for sampling from distributions and for optimization. In this work, we derive a closed-form expression for the expected loss of preconditioned LD near stationary points of the objective function. We use the fact that at the vicinity of such points, LD reduces to an Ornstein-Uhlenbeck process, which is amenable to convenient mathematical treatment. Our analysis reveals that when the preconditioning matrix satisfies a particular relation with respect to the noise covariance, LD's expected loss becomes proportional to the rank of the objective's Hessian. We illustrate the applicability of this result in the context of neural networks, where the Hessian rank has been shown to capture the complexity of the predictor function but is usually computationally hard to probe. Finally, we use our analysis to compare SGD-like and Adam-like preconditioners and identify the regimes under which each of them leads to a lower expected loss.

On Interference-Rejection using Riemannian Geometry for Direction of Arrival Estimation

We consider the problem of estimating the direction of arrival of desired acoustic sources in the presence of multiple acoustic interference sources. All the sources are located in noisy and reverberant environments and are received by a microphone array. We propose a new approach for designing beamformers based on the Riemannian geometry of the manifold of Hermitian positive definite matrices. Specifically, we show theoretically that incorporating the Riemannian mean of the spatial correlation matrices into frequently-used beamformers gives rise to beam patterns that reject the directions of interference sources and result in a higher signal-to-interference ratio. We experimentally demonstrate the advantages of our approach in designing several beamformers in the presence of simultaneously active multiple interference sources.

Option Discovery in the Absence of Rewards with Manifold Analysis

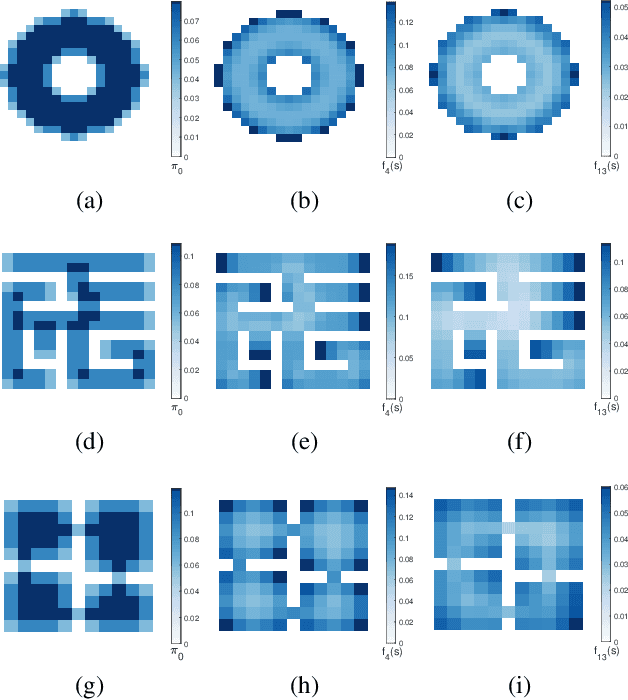
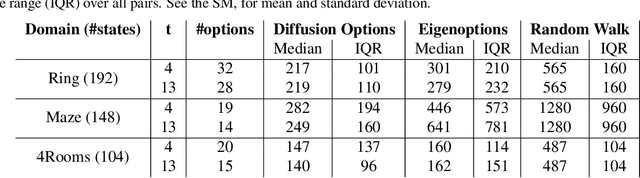
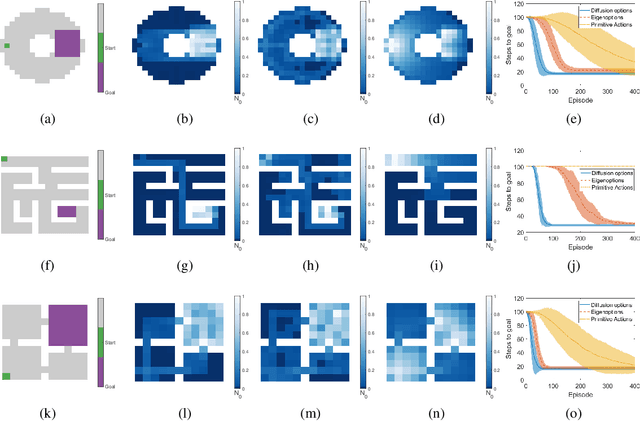
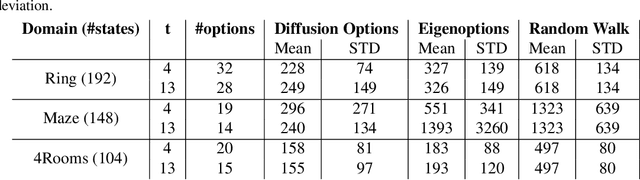
Options have been shown to be an effective tool in reinforcement learning, facilitating improved exploration and learning. In this paper, we present an approach based on spectral graph theory and derive an algorithm that systematically discovers options without access to a specific reward or task assignment. As opposed to the common practice used in previous methods, our algorithm makes full use of the spectrum of the graph Laplacian. Incorporating modes associated with higher graph frequencies unravels domain subtleties, which are shown to be useful for option discovery. Using geometric and manifold-based analysis, we present a theoretical justification for the algorithm. In addition, we showcase its performance in several domains, demonstrating clear improvements compared to competing methods.