Sleep Staging from Airflow Signals Using Fourier Approximations of Persistence Curves

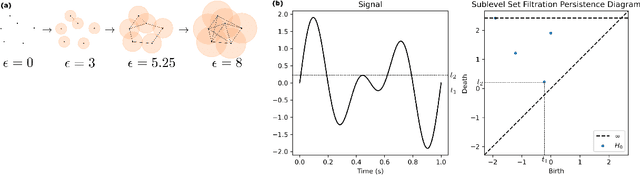
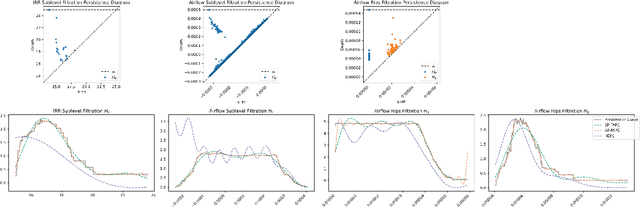
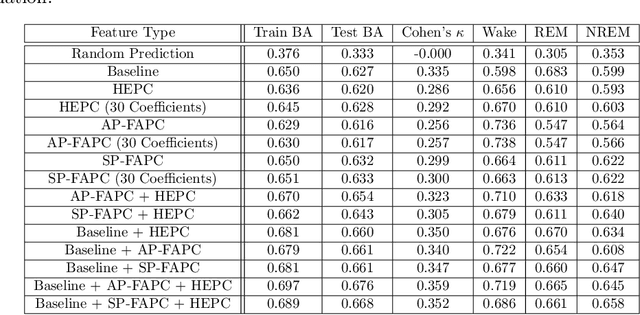
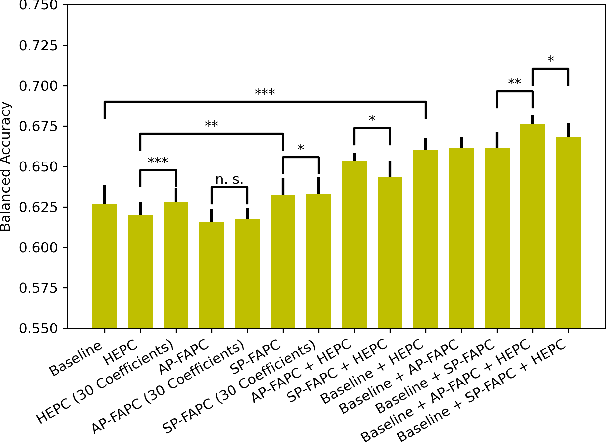
Sleep staging is a challenging task, typically manually performed by sleep technologists based on electroencephalogram and other biosignals of patients taken during overnight sleep studies. Recent work aims to leverage automated algorithms to perform sleep staging not based on electroencephalogram signals, but rather based on the airflow signals of subjects. Prior work uses ideas from topological data analysis (TDA), specifically Hermite function expansions of persistence curves (HEPC) to featurize airflow signals. However, finite order HEPC captures only partial information. In this work, we propose Fourier approximations of persistence curves (FAPC), and use this technique to perform sleep staging based on airflow signals. We analyze performance using an XGBoost model on 1155 pediatric sleep studies taken from the Nationwide Children's Hospital Sleep DataBank (NCHSDB), and find that FAPC methods provide complimentary information to HEPC methods alone, leading to a 4.9% increase in performance over baseline methods.

Landmark Alternating Diffusion

Alternating Diffusion (AD) is a commonly applied diffusion-based sensor fusion algorithm. While it has been successfully applied to various problems, its computational burden remains a limitation. Inspired by the landmark diffusion idea considered in the Robust and Scalable Embedding via Landmark Diffusion (ROSELAND), we propose a variation of AD, called Landmark AD (LAD), which captures the essence of AD while offering superior computational efficiency. We provide a series of theoretical analyses of LAD under the manifold setup and apply it to the automatic sleep stage annotation problem with two electroencephalogram channels to demonstrate its application.

Convergence analysis of t-SNE as a gradient flow for point cloud on a manifold

We present a theoretical foundation regarding the boundedness of the t-SNE algorithm. t-SNE employs gradient descent iteration with Kullback-Leibler (KL) divergence as the objective function, aiming to identify a set of points that closely resemble the original data points in a high-dimensional space, minimizing KL divergence. Investigating t-SNE properties such as perplexity and affinity under a weak convergence assumption on the sampled dataset, we examine the behavior of points generated by t-SNE under continuous gradient flow. Demonstrating that points generated by t-SNE remain bounded, we leverage this insight to establish the existence of a minimizer for KL divergence.

Design a Metric Robust to Complicated High Dimensional Noise for Efficient Manifold Denoising

In this manuscript, we propose an efficient manifold denoiser based on landmark diffusion and optimal shrinkage under the complicated high dimensional noise and compact manifold setup. It is flexible to handle several setups, including the high ambient space dimension with a manifold embedding that occupies a subspace of high or low dimensions, and the noise could be colored and dependent. A systematic comparison with other existing algorithms on both simulated and real datasets is provided. This manuscript is mainly algorithmic and we report several existing tools and numerical results. Theoretical guarantees and more comparisons will be reported in the official paper of this manuscript.

Unveil Sleep Spindles with Concentration of Frequency and Time

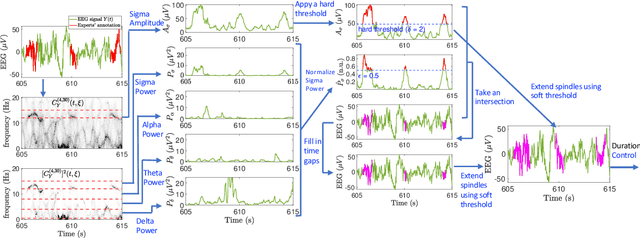
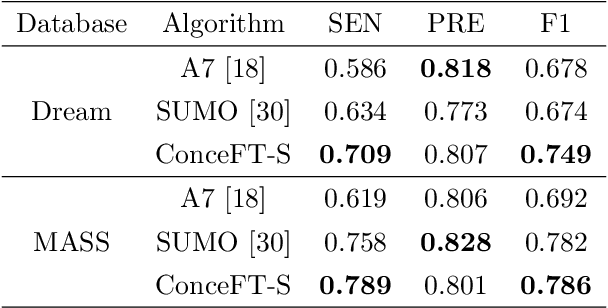
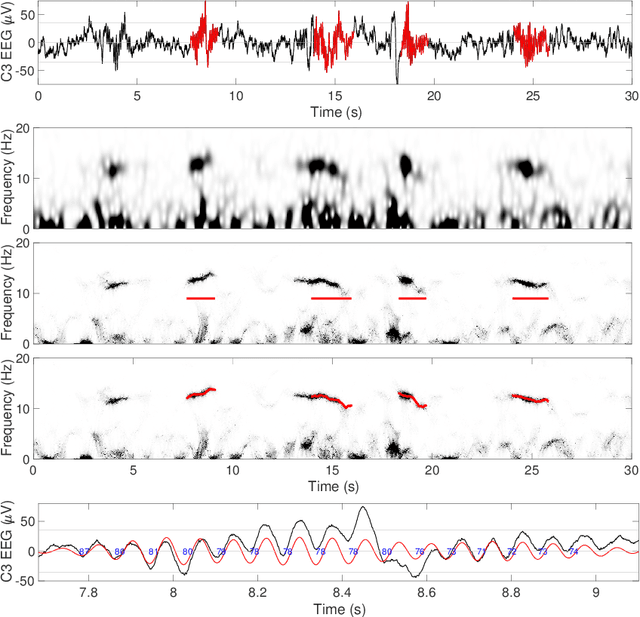
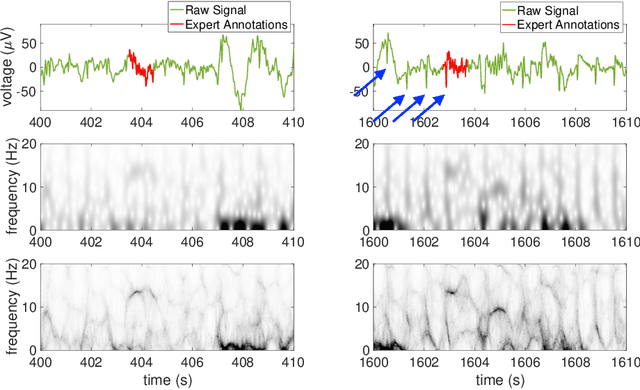
Objective: Sleep spindles contain crucial brain dynamics information. We introduce the novel non-linear time-frequency analysis tool 'Concentration of Frequency and Time' (ConceFT) to create an interpretable automated algorithm for sleep spindle annotation in EEG data and to measure spindle instantaneous frequencies (IFs). Methods: ConceFT effectively reduces stochastic EEG influence, enhancing spindle visibility in the time-frequency representation. Our automated spindle detection algorithm, ConceFT-Spindle (ConceFT-S), is compared to A7 (non-deep learning) and SUMO (deep learning) using Dream and MASS benchmark databases. We also quantify spindle IF dynamics. Results: ConceFT-S achieves F1 scores of 0.749 in Dream and 0.786 in MASS, which is equivalent to or surpass A7 and SUMO with statistical significance. We reveal that spindle IF is generally nonlinear. Conclusion: ConceFT offers an accurate, interpretable EEG-based sleep spindle detection algorithm and enables spindle IF quantification.

Geometric Scattering on Measure Spaces

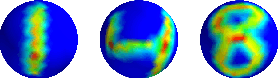
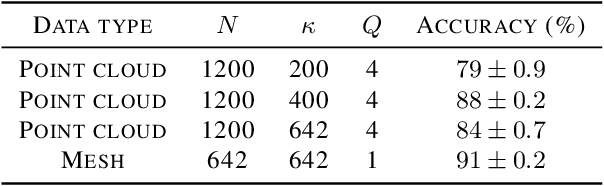
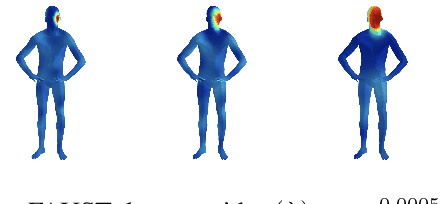
The scattering transform is a multilayered, wavelet-based transform initially introduced as a model of convolutional neural networks (CNNs) that has played a foundational role in our understanding of these networks' stability and invariance properties. Subsequently, there has been widespread interest in extending the success of CNNs to data sets with non-Euclidean structure, such as graphs and manifolds, leading to the emerging field of geometric deep learning. In order to improve our understanding of the architectures used in this new field, several papers have proposed generalizations of the scattering transform for non-Euclidean data structures such as undirected graphs and compact Riemannian manifolds without boundary. In this paper, we introduce a general, unified model for geometric scattering on measure spaces. Our proposed framework includes previous work on geometric scattering as special cases but also applies to more general settings such as directed graphs, signed graphs, and manifolds with boundary. We propose a new criterion that identifies to which groups a useful representation should be invariant and show that this criterion is sufficient to guarantee that the scattering transform has desirable stability and invariance properties. Additionally, we consider finite measure spaces that are obtained from randomly sampling an unknown manifold. We propose two methods for constructing a data-driven graph on which the associated graph scattering transform approximates the scattering transform on the underlying manifold. Moreover, we use a diffusion-maps based approach to prove quantitative estimates on the rate of convergence of one of these approximations as the number of sample points tends to infinity. Lastly, we showcase the utility of our method on spherical images, directed graphs, and on high-dimensional single-cell data.

An iterative warping and clustering algorithm to estimate multiple wave-shape functions from a nonstationary oscillatory signal

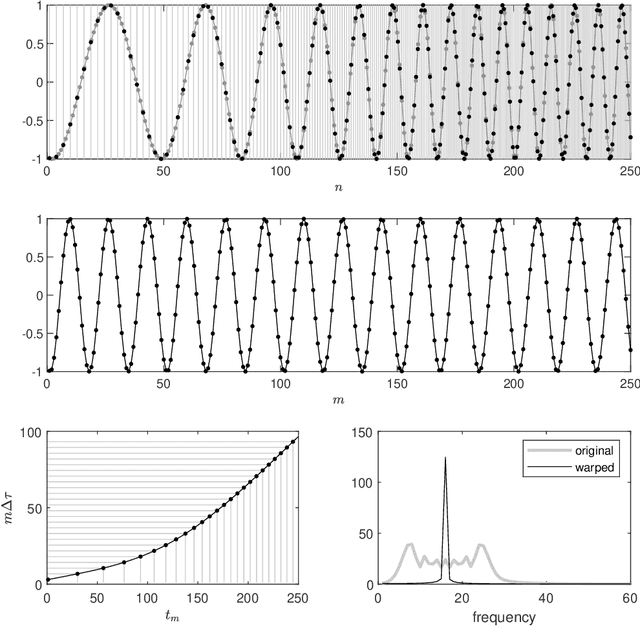
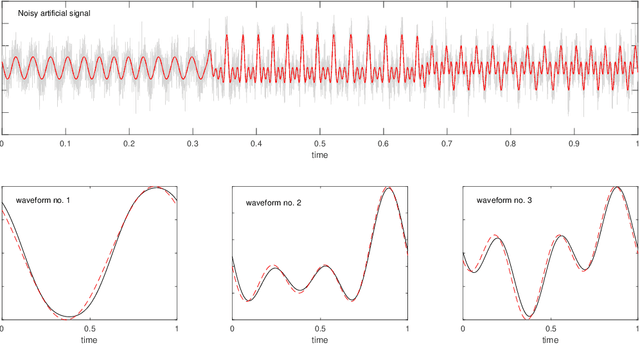
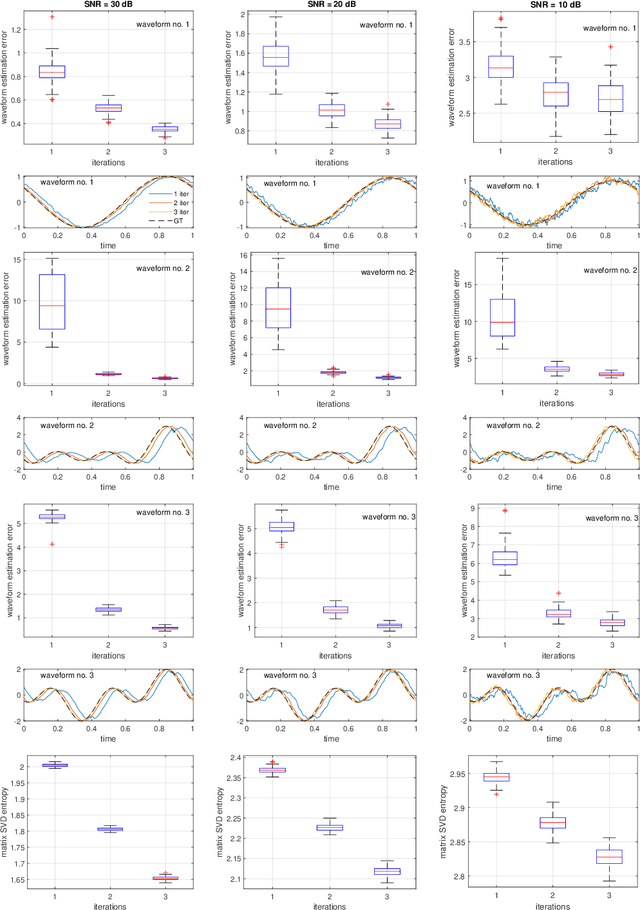
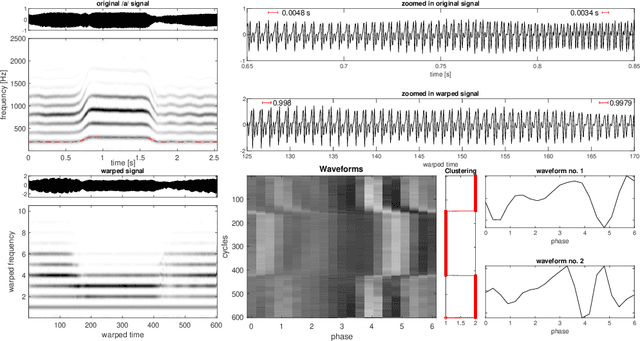
We present an algorithm to estimate multiple wave-shape functions (WSF) from a nonstationary oscillatory signal with time-varying amplitude and frequency. Suppose there are finite different $1$-periodic functions, $s_1,\ldots,s_K$, as WSFs that model different oscillatory patterns in an oscillatory signal, where the WSF might jump from one to another suddenly. The proposed algorithm detects change points and estimates $s_1,\ldots,s_K$ from the signal by a novel iterative warping and clustering algorithm, which is a combination of time-frequency analysis, singular value decomposition entropy and vector spectral clustering. We demonstrate the efficiency of the proposed algorithm with simulated and real signals, including the voice signal, arterial blood pressure, electrocardiogram and accelerometer signal. Moreover, we provide a mathematical justification of the algorithm under the assumption that the amplitude and frequency of the signal are slowly time-varying and there are finite change points that model sudden changes from one wave-shape function to another one.

The Manifold Scattering Transform for High-Dimensional Point Cloud Data

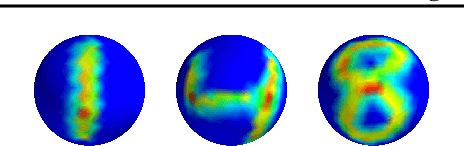
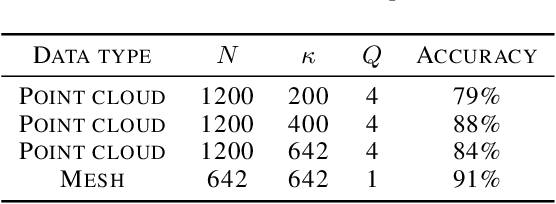
The manifold scattering transform is a deep feature extractor for data defined on a Riemannian manifold. It is one of the first examples of extending convolutional neural network-like operators to general manifolds. The initial work on this model focused primarily on its theoretical stability and invariance properties but did not provide methods for its numerical implementation except in the case of two-dimensional surfaces with predefined meshes. In this work, we present practical schemes, based on the theory of diffusion maps, for implementing the manifold scattering transform to datasets arising in naturalistic systems, such as single cell genetics, where the data is a high-dimensional point cloud modeled as lying on a low-dimensional manifold. We show that our methods are effective for signal classification and manifold classification tasks.

Spatiotemporal Analysis Using Riemannian Composition of Diffusion Operators

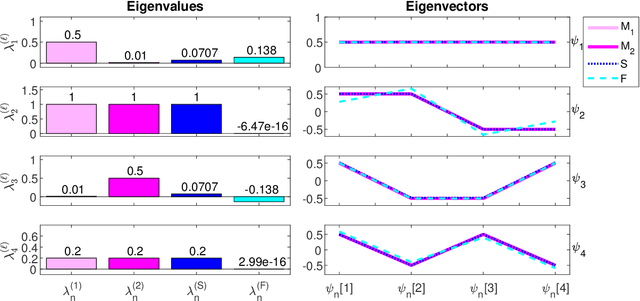
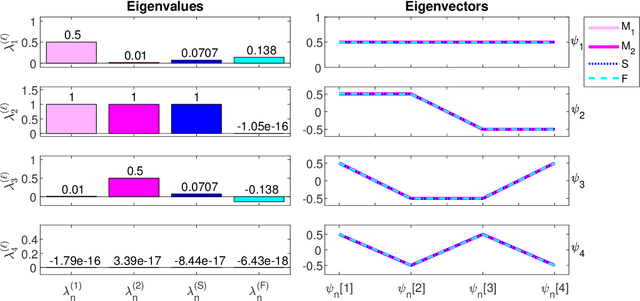
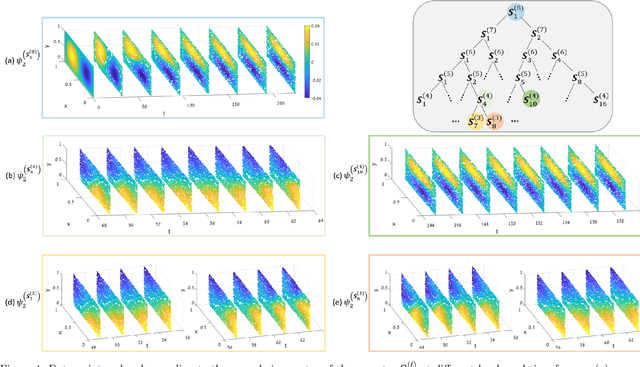
Multivariate time-series have become abundant in recent years, as many data-acquisition systems record information through multiple sensors simultaneously. In this paper, we assume the variables pertain to some geometry and present an operator-based approach for spatiotemporal analysis. Our approach combines three components that are often considered separately: (i) manifold learning for building operators representing the geometry of the variables, (ii) Riemannian geometry of symmetric positive-definite matrices for multiscale composition of operators corresponding to different time samples, and (iii) spectral analysis of the composite operators for extracting different dynamic modes. We propose a method that is analogous to the classical wavelet analysis, which we term Riemannian multi-resolution analysis (RMRA). We provide some theoretical results on the spectral analysis of the composite operators, and we demonstrate the proposed method on simulations and on real data.

Predicting Trust Using Automated Assessment of Multivariate Interactional Synchrony

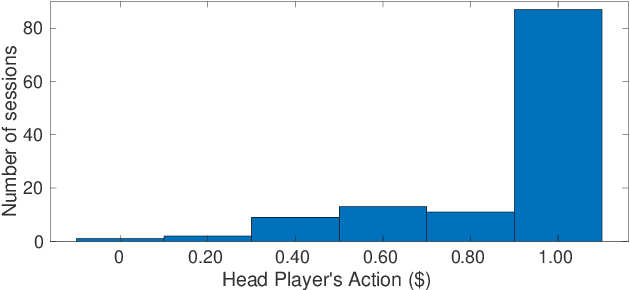
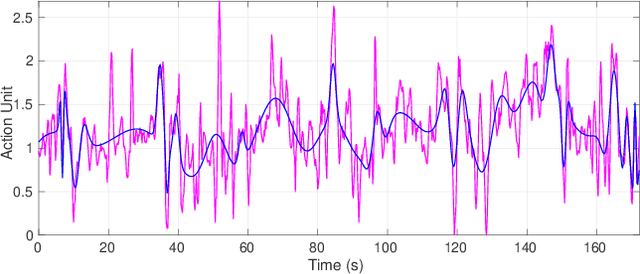
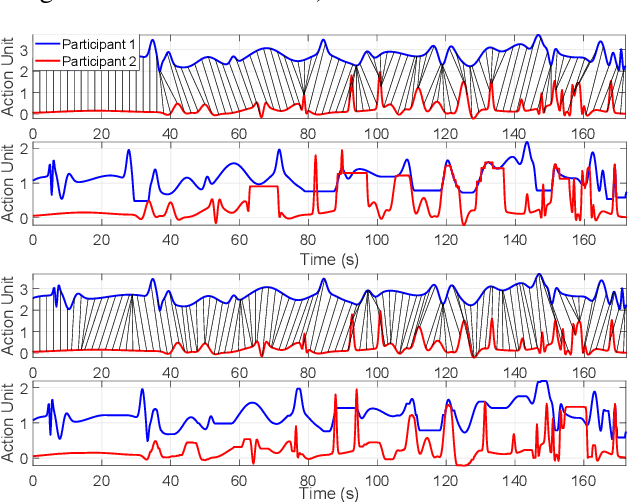
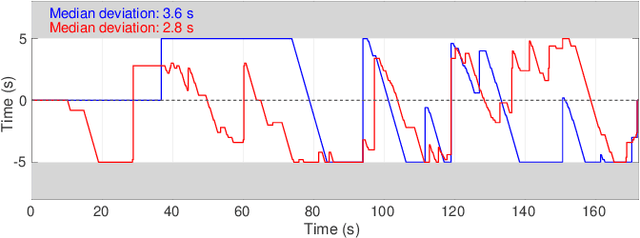
Diverse disciplines are interested in how the coordination of interacting agents' movements, emotions, and physiology over time impacts social behavior. Here, we describe a new multivariate procedure for automating the investigation of this kind of behaviorally-relevant "interactional synchrony", and introduce a novel interactional synchrony measure based on features of dynamic time warping (DTW) paths. We demonstrate that our DTW path-based measure of interactional synchrony between facial action units of two people interacting freely in a natural social interaction can be used to predict how much trust they will display in a subsequent Trust Game. We also show that our approach outperforms univariate head movement models, models that consider participants' facial action units independently, and models that use previously proposed synchrony or similarity measures. The insights of this work can be applied to any research question that aims to quantify the temporal coordination of multiple signals over time, but has immediate applications in psychology, medicine, and robotics.