An iterative warping and clustering algorithm to estimate multiple wave-shape functions from a nonstationary oscillatory signal

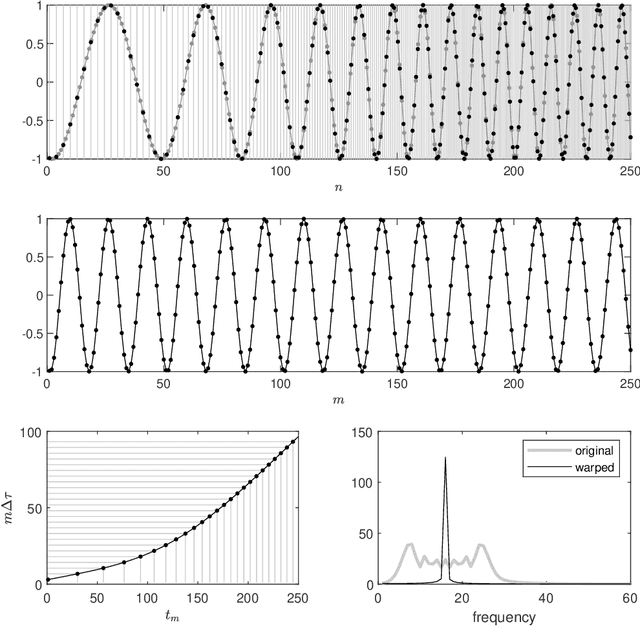
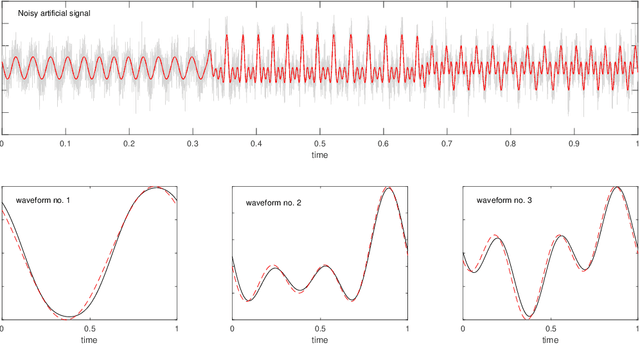
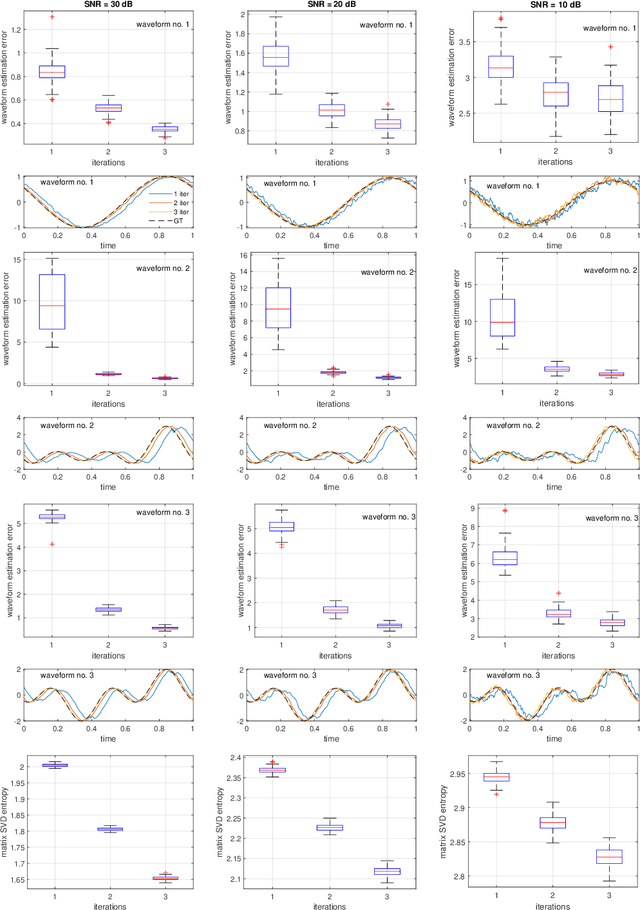
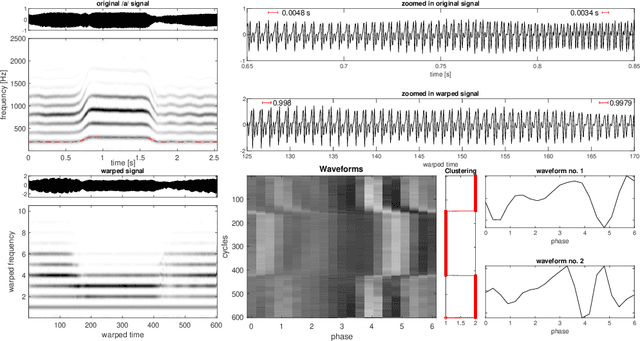
We present an algorithm to estimate multiple wave-shape functions (WSF) from a nonstationary oscillatory signal with time-varying amplitude and frequency. Suppose there are finite different $1$-periodic functions, $s_1,\ldots,s_K$, as WSFs that model different oscillatory patterns in an oscillatory signal, where the WSF might jump from one to another suddenly. The proposed algorithm detects change points and estimates $s_1,\ldots,s_K$ from the signal by a novel iterative warping and clustering algorithm, which is a combination of time-frequency analysis, singular value decomposition entropy and vector spectral clustering. We demonstrate the efficiency of the proposed algorithm with simulated and real signals, including the voice signal, arterial blood pressure, electrocardiogram and accelerometer signal. Moreover, we provide a mathematical justification of the algorithm under the assumption that the amplitude and frequency of the signal are slowly time-varying and there are finite change points that model sudden changes from one wave-shape function to another one.