MDNF: Multi-Diffusion-Nets for Neural Fields on Meshes

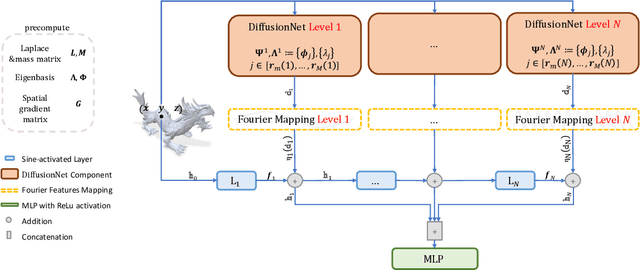
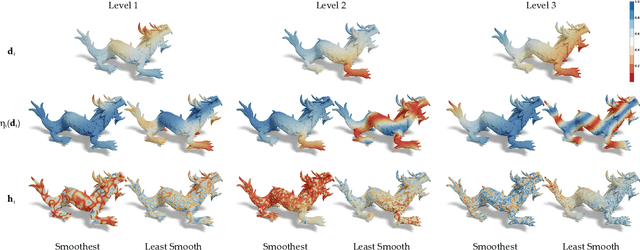
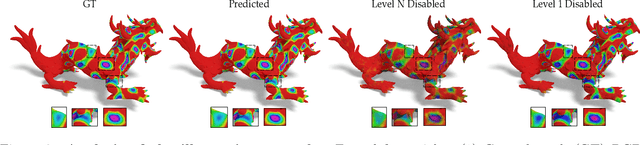
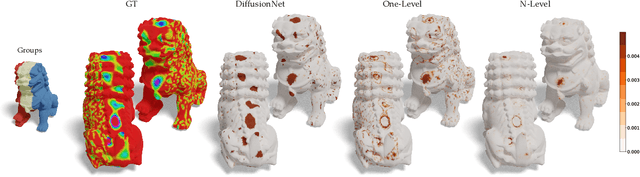
We propose a novel framework for representing neural fields on triangle meshes that is multi-resolution across both spatial and frequency domains. Inspired by the Neural Fourier Filter Bank (NFFB), our architecture decomposes the spatial and frequency domains by associating finer spatial resolution levels with higher frequency bands, while coarser resolutions are mapped to lower frequencies. To achieve geometry-aware spatial decomposition we leverage multiple DiffusionNet components, each associated with a different spatial resolution level. Subsequently, we apply a Fourier feature mapping to encourage finer resolution levels to be associated with higher frequencies. The final signal is composed in a wavelet-inspired manner using a sine-activated MLP, aggregating higher-frequency signals on top of lower-frequency ones. Our architecture attains high accuracy in learning complex neural fields and is robust to discontinuities, exponential scale variations of the target field, and mesh modification. We demonstrate the effectiveness of our approach through its application to diverse neural fields, such as synthetic RGB functions, UV texture coordinates, and vertex normals, illustrating different challenges. To validate our method, we compare its performance against two alternatives, showcasing the advantages of our multi-resolution architecture.

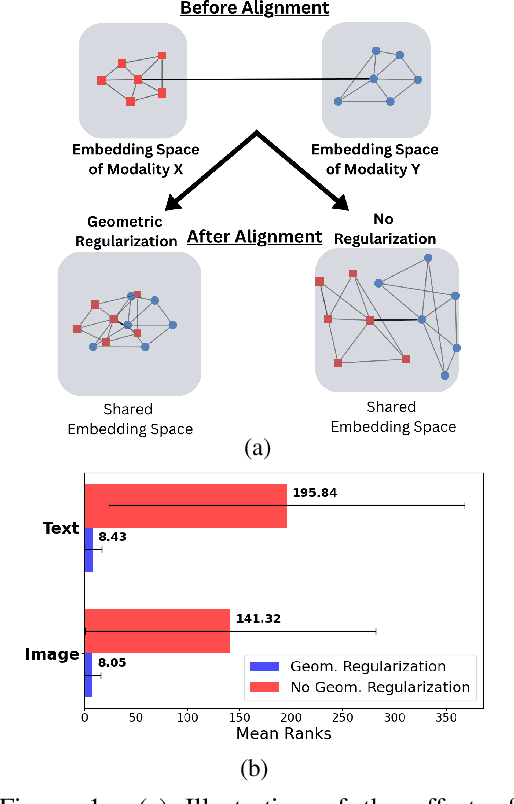
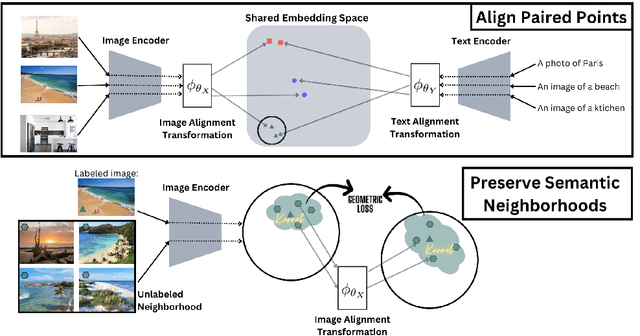
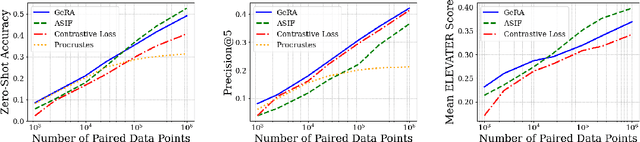
GeRA: Label-Efficient Geometrically Regularized Alignment

Pretrained unimodal encoders incorporate rich semantic information into embedding space structures. To be similarly informative, multi-modal encoders typically require massive amounts of paired data for alignment and training. We introduce a semi-supervised Geometrically Regularized Alignment (GeRA) method to align the embedding spaces of pretrained unimodal encoders in a label-efficient way. Our method leverages the manifold geometry of unpaired (unlabeled) data to improve alignment performance. To prevent distortions to local geometry during the alignment process, potentially disrupting semantic neighborhood structures and causing misalignment of unobserved pairs, we introduce a geometric loss term. This term is built upon a diffusion operator that captures the local manifold geometry of the unimodal pretrained encoders. GeRA is modality-agnostic and thus can be used to align pretrained encoders from any data modalities. We provide empirical evidence to the effectiveness of our method in the domains of speech-text and image-text alignment. Our experiments demonstrate significant improvement in alignment quality compared to a variaty of leading baselines, especially with a small amount of paired data, using our proposed geometric regularization.

Large Language Model Routing with Benchmark Datasets

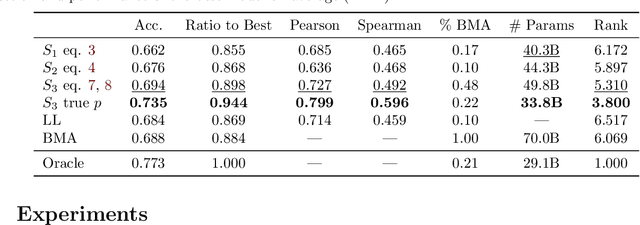
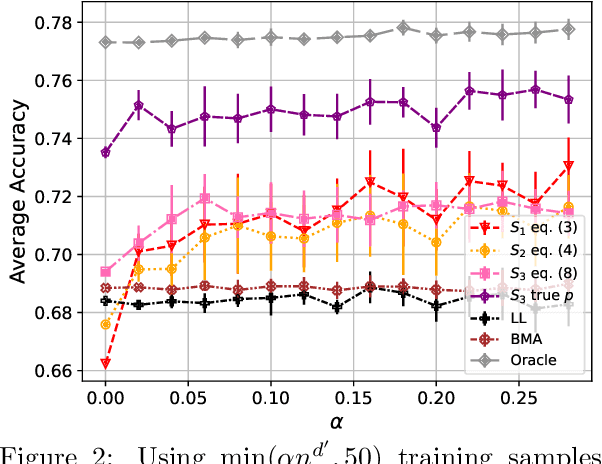
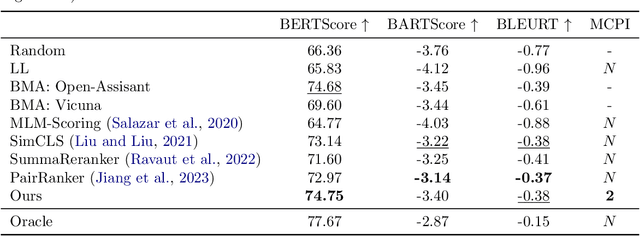
There is a rapidly growing number of open-source Large Language Models (LLMs) and benchmark datasets to compare them. While some models dominate these benchmarks, no single model typically achieves the best accuracy in all tasks and use cases. In this work, we address the challenge of selecting the best LLM out of a collection of models for new tasks. We propose a new formulation for the problem, in which benchmark datasets are repurposed to learn a "router" model for this LLM selection, and we show that this problem can be reduced to a collection of binary classification tasks. We demonstrate the utility and limitations of learning model routers from various benchmark datasets, where we consistently improve performance upon using any single model for all tasks.

ManiFeSt: Manifold-based Feature Selection for Small Data Sets

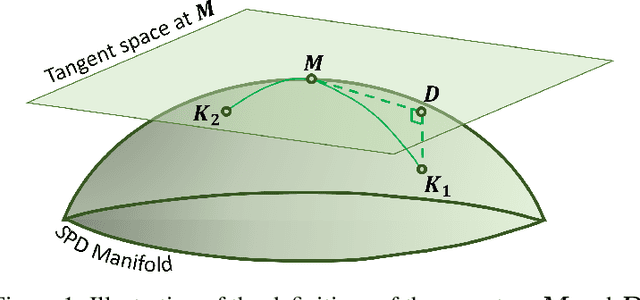
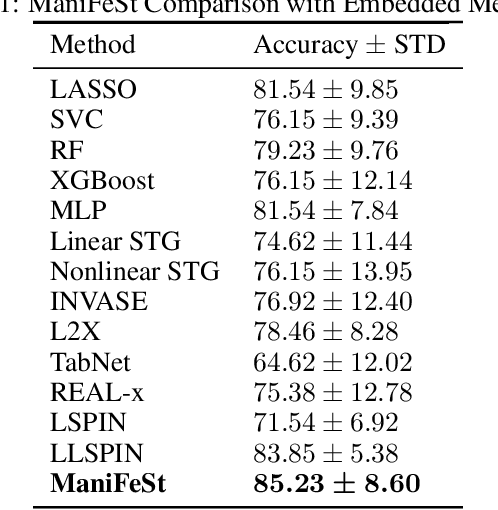
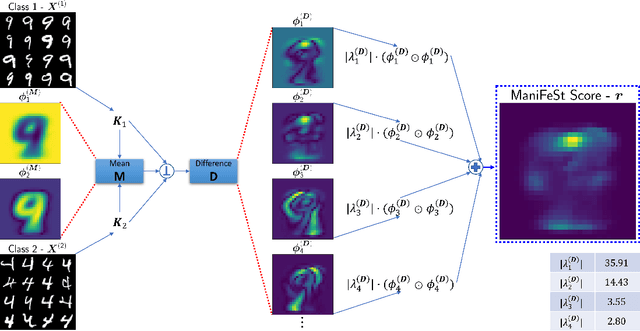
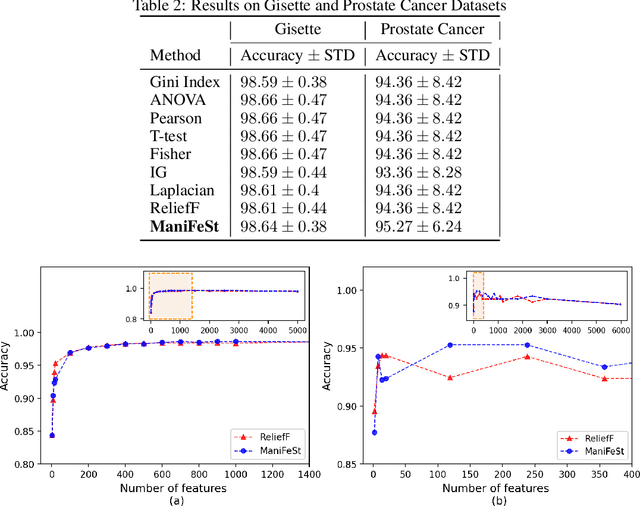
In this paper, we present a new method for few-sample supervised feature selection (FS). Our method first learns the manifold of the feature space of each class using kernels capturing multi-feature associations. Then, based on Riemannian geometry, a composite kernel is computed, extracting the differences between the learned feature associations. Finally, a FS score based on spectral analysis is proposed. Considering multi-feature associations makes our method multivariate by design. This in turn allows for the extraction of the hidden manifold underlying the features and avoids overfitting, facilitating few-sample FS. We showcase the efficacy of our method on illustrative examples and several benchmarks, where our method demonstrates higher accuracy in selecting the informative features compared to competing methods. In addition, we show that our FS leads to improved classification and better generalization when applied to test data.

Log-Euclidean Signatures for Intrinsic Distances Between Unaligned Datasets

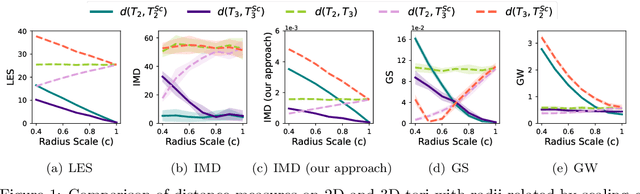
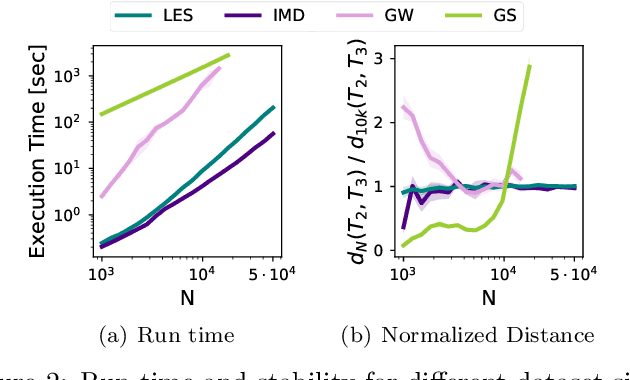
The need for efficiently comparing and representing datasets with unknown alignment spans various fields, from model analysis and comparison in machine learning to trend discovery in collections of medical datasets. We use manifold learning to compare the intrinsic geometric structures of different datasets by comparing their diffusion operators, symmetric positive-definite (SPD) matrices that relate to approximations of the continuous Laplace-Beltrami operator from discrete samples. Existing methods typically compare such operators in a pointwise manner or assume known data alignment. Instead, we exploit the Riemannian geometry of SPD matrices to compare these operators and define a new theoretically-motivated distance based on a lower bound of the log-Euclidean metric. Our framework facilitates comparison of data manifolds expressed in datasets with different sizes, numbers of features, and measurement modalities. Our log-Euclidean signature (LES) distance recovers meaningful structural differences, outperforming competing methods in various application domains.

Spatiotemporal Analysis Using Riemannian Composition of Diffusion Operators

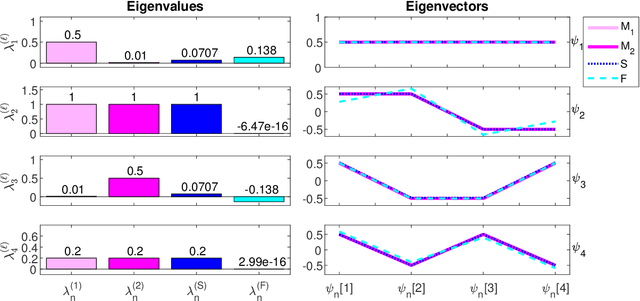
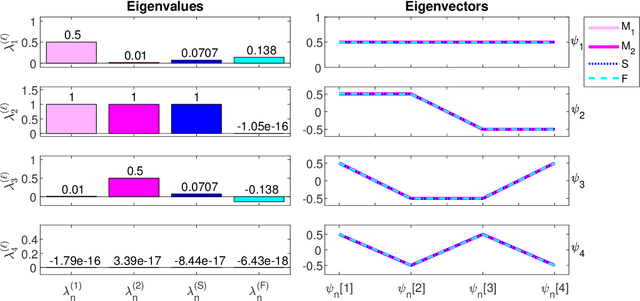
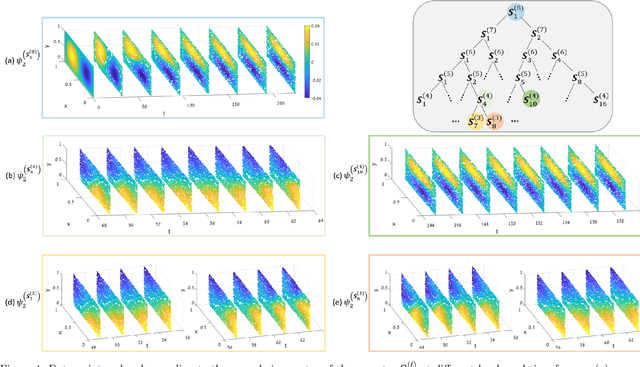
Multivariate time-series have become abundant in recent years, as many data-acquisition systems record information through multiple sensors simultaneously. In this paper, we assume the variables pertain to some geometry and present an operator-based approach for spatiotemporal analysis. Our approach combines three components that are often considered separately: (i) manifold learning for building operators representing the geometry of the variables, (ii) Riemannian geometry of symmetric positive-definite matrices for multiscale composition of operators corresponding to different time samples, and (iii) spectral analysis of the composite operators for extracting different dynamic modes. We propose a method that is analogous to the classical wavelet analysis, which we term Riemannian multi-resolution analysis (RMRA). We provide some theoretical results on the spectral analysis of the composite operators, and we demonstrate the proposed method on simulations and on real data.