FRIDU: Functional Map Refinement with Guided Image Diffusion

We propose a novel approach for refining a given correspondence map between two shapes. A correspondence map represented as a functional map, namely a change of basis matrix, can be additionally treated as a 2D image. With this perspective, we train an image diffusion model directly in the space of functional maps, enabling it to generate accurate maps conditioned on an inaccurate initial map. The training is done purely in the functional space, and thus is highly efficient. At inference time, we use the pointwise map corresponding to the current functional map as guidance during the diffusion process. The guidance can additionally encourage different functional map objectives, such as orthogonality and commutativity with the Laplace-Beltrami operator. We show that our approach is competitive with state-of-the-art methods of map refinement and that guided diffusion models provide a promising pathway to functional map processing.

MDNF: Multi-Diffusion-Nets for Neural Fields on Meshes

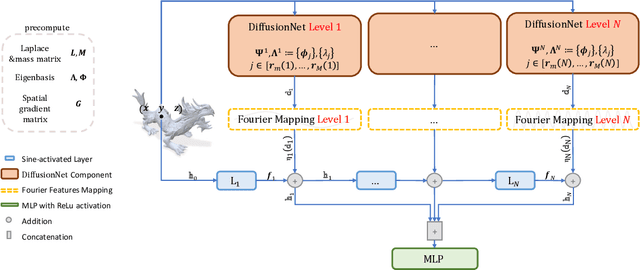
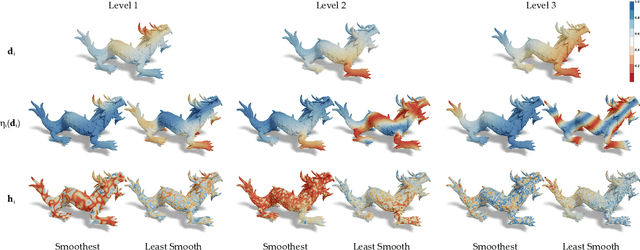
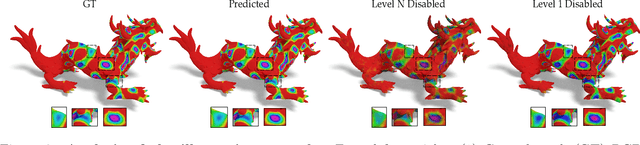
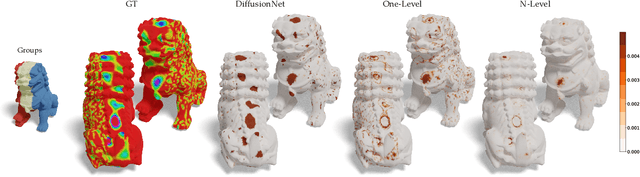
We propose a novel framework for representing neural fields on triangle meshes that is multi-resolution across both spatial and frequency domains. Inspired by the Neural Fourier Filter Bank (NFFB), our architecture decomposes the spatial and frequency domains by associating finer spatial resolution levels with higher frequency bands, while coarser resolutions are mapped to lower frequencies. To achieve geometry-aware spatial decomposition we leverage multiple DiffusionNet components, each associated with a different spatial resolution level. Subsequently, we apply a Fourier feature mapping to encourage finer resolution levels to be associated with higher frequencies. The final signal is composed in a wavelet-inspired manner using a sine-activated MLP, aggregating higher-frequency signals on top of lower-frequency ones. Our architecture attains high accuracy in learning complex neural fields and is robust to discontinuities, exponential scale variations of the target field, and mesh modification. We demonstrate the effectiveness of our approach through its application to diverse neural fields, such as synthetic RGB functions, UV texture coordinates, and vertex normals, illustrating different challenges. To validate our method, we compare its performance against two alternatives, showcasing the advantages of our multi-resolution architecture.