Likelihood Training of Cascaded Diffusion Models via Hierarchical Volume-preserving Maps

Cascaded models are multi-scale generative models with a marked capacity for producing perceptually impressive samples at high resolutions. In this work, we show that they can also be excellent likelihood models, so long as we overcome a fundamental difficulty with probabilistic multi-scale models: the intractability of the likelihood function. Chiefly, in cascaded models each intermediary scale introduces extraneous variables that cannot be tractably marginalized out for likelihood evaluation. This issue vanishes by modeling the diffusion process on latent spaces induced by a class of transformations we call hierarchical volume-preserving maps, which decompose spatially structured data in a hierarchical fashion without introducing local distortions in the latent space. We demonstrate that two such maps are well-known in the literature for multiscale modeling: Laplacian pyramids and wavelet transforms. Not only do such reparameterizations allow the likelihood function to be directly expressed as a joint likelihood over the scales, we show that the Laplacian pyramid and wavelet transform also produces significant improvements to the state-of-the-art on a selection of benchmarks in likelihood modeling, including density estimation, lossless compression, and out-of-distribution detection. Investigating the theoretical basis of our empirical gains we uncover deep connections to score matching under the Earth Mover's Distance (EMD), which is a well-known surrogate for perceptual similarity. Code can be found at \href{https://github.com/lihenryhfl/pcdm}{this https url}.

Dual Diffusion for Unified Image Generation and Understanding

Diffusion models have gained tremendous success in text-to-image generation, yet still lag behind with visual understanding tasks, an area dominated by autoregressive vision-language models. We propose a large-scale and fully end-to-end diffusion model for multi-modal understanding and generation that significantly improves on existing diffusion-based multimodal models, and is the first of its kind to support the full suite of vision-language modeling capabilities. Inspired by the multimodal diffusion transformer (MM-DiT) and recent advances in discrete diffusion language modeling, we leverage a cross-modal maximum likelihood estimation framework that simultaneously trains the conditional likelihoods of both images and text jointly under a single loss function, which is back-propagated through both branches of the diffusion transformer. The resulting model is highly flexible and capable of a wide range of tasks including image generation, captioning, and visual question answering. Our model attained competitive performance compared to recent unified image understanding and generation models, demonstrating the potential of multimodal diffusion modeling as a promising alternative to autoregressive next-token prediction models.

Entropic Optimal Transport Eigenmaps for Nonlinear Alignment and Joint Embedding of High-Dimensional Datasets

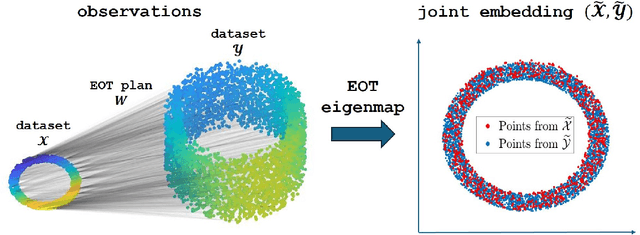
Embedding high-dimensional data into a low-dimensional space is an indispensable component of data analysis. In numerous applications, it is necessary to align and jointly embed multiple datasets from different studies or experimental conditions. Such datasets may share underlying structures of interest but exhibit individual distortions, resulting in misaligned embeddings using traditional techniques. In this work, we propose \textit{Entropic Optimal Transport (EOT) eigenmaps}, a principled approach for aligning and jointly embedding a pair of datasets with theoretical guarantees. Our approach leverages the leading singular vectors of the EOT plan matrix between two datasets to extract their shared underlying structure and align the datasets accordingly in a common embedding space. We interpret our approach as an inter-data variant of the classical Laplacian eigenmaps and diffusion maps embeddings, showing that it enjoys many favorable analogous properties. We then analyze a data-generative model where two observed high-dimensional datasets share latent variables on a common low-dimensional manifold, but each dataset is subject to data-specific translation, scaling, nuisance structures, and noise. We show that in a high-dimensional asymptotic regime, the EOT plan recovers the shared manifold structure by approximating a kernel function evaluated at the locations of the latent variables. Subsequently, we provide a geometric interpretation of our embedding by relating it to the eigenfunctions of population-level operators encoding the density and geometry of the shared manifold. Finally, we showcase the performance of our approach for data integration and embedding through simulations and analyses of real-world biological data, demonstrating its advantages over alternative methods in challenging scenarios.

Exponential weight averaging as damped harmonic motion

The exponential moving average (EMA) is a commonly used statistic for providing stable estimates of stochastic quantities in deep learning optimization. Recently, EMA has seen considerable use in generative models, where it is computed with respect to the model weights, and significantly improves the stability of the inference model during and after training. While the practice of weight averaging at the end of training is well-studied and known to improve estimates of local optima, the benefits of EMA over the course of training is less understood. In this paper, we derive an explicit connection between EMA and a damped harmonic system between two particles, where one particle (the EMA weights) is drawn to the other (the model weights) via an idealized zero-length spring. We then leverage this physical analogy to analyze the effectiveness of EMA, and propose an improved training algorithm, which we call BELAY. Finally, we demonstrate theoretically and empirically several advantages enjoyed by BELAY over standard EMA.

Multi-modal Differentiable Unsupervised Feature Selection

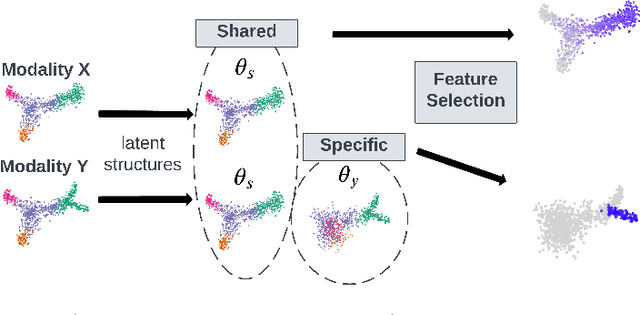
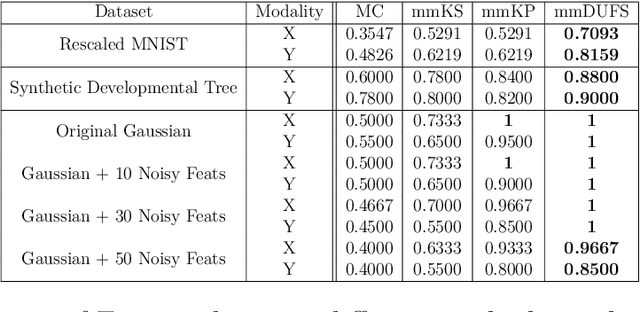
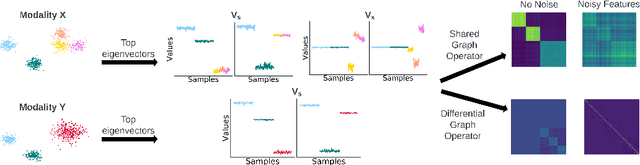
Multi-modal high throughput biological data presents a great scientific opportunity and a significant computational challenge. In multi-modal measurements, every sample is observed simultaneously by two or more sets of sensors. In such settings, many observed variables in both modalities are often nuisance and do not carry information about the phenomenon of interest. Here, we propose a multi-modal unsupervised feature selection framework: identifying informative variables based on coupled high-dimensional measurements. Our method is designed to identify features associated with two types of latent low-dimensional structures: (i) shared structures that govern the observations in both modalities and (ii) differential structures that appear in only one modality. To that end, we propose two Laplacian-based scoring operators. We incorporate the scores with differentiable gates that mask nuisance features and enhance the accuracy of the structure captured by the graph Laplacian. The performance of the new scheme is illustrated using synthetic and real datasets, including an extended biological application to single-cell multi-omics.

Autoregressive Generative Modeling with Noise Conditional Maximum Likelihood Estimation

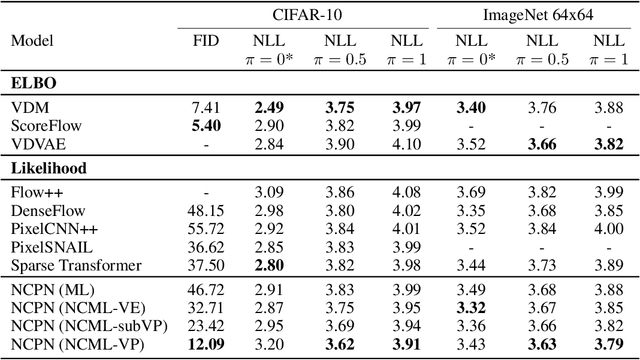
We introduce a simple modification to the standard maximum likelihood estimation (MLE) framework. Rather than maximizing a single unconditional likelihood of the data under the model, we maximize a family of \textit{noise conditional} likelihoods consisting of the data perturbed by a continuum of noise levels. We find that models trained this way are more robust to noise, obtain higher test likelihoods, and generate higher quality images. They can also be sampled from via a novel score-based sampling scheme which combats the classical \textit{covariate shift} problem that occurs during sample generation in autoregressive models. Applying this augmentation to autoregressive image models, we obtain 3.32 bits per dimension on the ImageNet 64x64 dataset, and substantially improve the quality of generated samples in terms of the Frechet Inception distance (FID) -- from 37.50 to 12.09 on the CIFAR-10 dataset.

ManiFeSt: Manifold-based Feature Selection for Small Data Sets

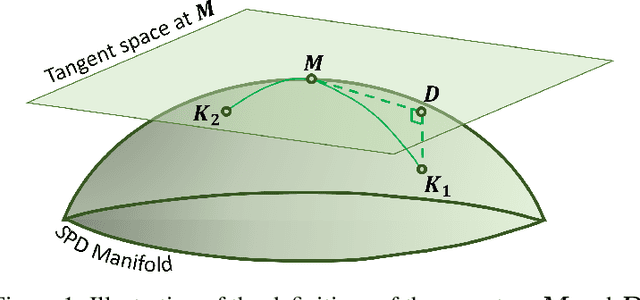
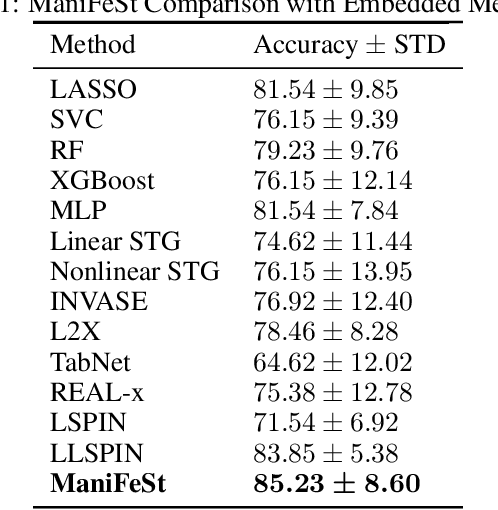
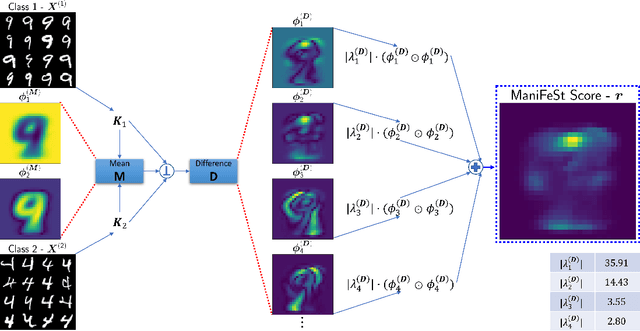
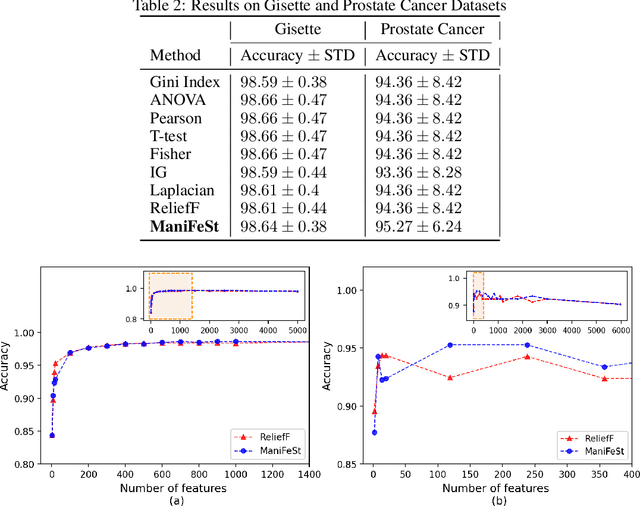
In this paper, we present a new method for few-sample supervised feature selection (FS). Our method first learns the manifold of the feature space of each class using kernels capturing multi-feature associations. Then, based on Riemannian geometry, a composite kernel is computed, extracting the differences between the learned feature associations. Finally, a FS score based on spectral analysis is proposed. Considering multi-feature associations makes our method multivariate by design. This in turn allows for the extraction of the hidden manifold underlying the features and avoids overfitting, facilitating few-sample FS. We showcase the efficacy of our method on illustrative examples and several benchmarks, where our method demonstrates higher accuracy in selecting the informative features compared to competing methods. In addition, we show that our FS leads to improved classification and better generalization when applied to test data.

Neural Inverse Transform Sampler

Any explicit functional representation $f$ of a density is hampered by two main obstacles when we wish to use it as a generative model: designing $f$ so that sampling is fast, and estimating $Z = \int f$ so that $Z^{-1}f$ integrates to 1. This becomes increasingly complicated as $f$ itself becomes complicated. In this paper, we show that when modeling one-dimensional conditional densities with a neural network, $Z$ can be exactly and efficiently computed by letting the network represent the cumulative distribution function of a target density, and applying a generalized fundamental theorem of calculus. We also derive a fast algorithm for sampling from the resulting representation by the inverse transform method. By extending these principles to higher dimensions, we introduce the \textbf{Neural Inverse Transform Sampler (NITS)}, a novel deep learning framework for modeling and sampling from general, multidimensional, compactly-supported probability densities. NITS is a highly expressive density estimator that boasts end-to-end differentiability, fast sampling, and exact and cheap likelihood evaluation. We demonstrate the applicability of NITS by applying it to realistic, high-dimensional density estimation tasks: likelihood-based generative modeling on the CIFAR-10 dataset, and density estimation on the UCI suite of benchmark datasets, where NITS produces compelling results rivaling or surpassing the state of the art.

Deep Unsupervised Feature Selection by Discarding Nuisance and Correlated Features

Modern datasets often contain large subsets of correlated features and nuisance features, which are not or loosely related to the main underlying structures of the data. Nuisance features can be identified using the Laplacian score criterion, which evaluates the importance of a given feature via its consistency with the Graph Laplacians' leading eigenvectors. We demonstrate that in the presence of large numbers of nuisance features, the Laplacian must be computed on the subset of selected features rather than on the complete feature set. To do this, we propose a fully differentiable approach for unsupervised feature selection, utilizing the Laplacian score criterion to avoid the selection of nuisance features. We employ an autoencoder architecture to cope with correlated features, trained to reconstruct the data from the subset of selected features. Building on the recently proposed concrete layer that allows controlling for the number of selected features via architectural design, simplifying the optimization process. Experimenting on several real-world datasets, we demonstrate that our proposed approach outperforms similar approaches designed to avoid only correlated or nuisance features, but not both. Several state-of-the-art clustering results are reported.

Probabilistic Robust Autoencoders for Anomaly Detection

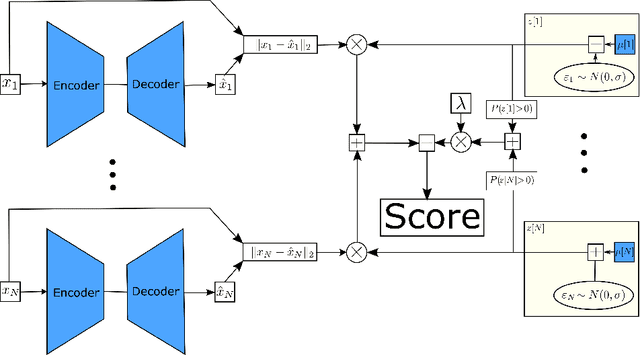
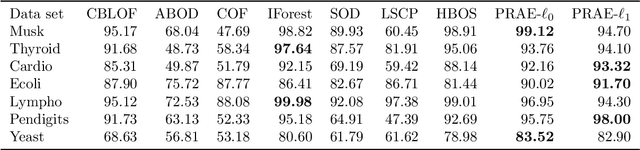
Empirical observations often consist of anomalies (or outliers) that contaminate the data. Accurate identification of anomalous samples is crucial for the success of downstream data analysis tasks. To automatically identify anomalies, we propose a new type of autoencoder (AE) which we term Probabilistic Robust autoencoder (PRAE). PRAE is designed to simultaneously remove outliers and identify a low-dimensional representation for the inlier samples. We first describe Robust AE (RAE) as a model that aims to split the data to inlier samples from which a low dimensional representation is learned via an AE, and anomalous (outlier) samples that are excluded as they do not fit the low dimensional representation. Robust AE minimizes the reconstruction of the AE while attempting to incorporate as many observations as possible. This could be realized by subtracting from the reconstruction term an $\ell_0$ norm counting the number of selected observations. Since the $\ell_0$ norm is not differentiable, we propose two probabilistic relaxations for the RAE approach and demonstrate that they can effectively identify anomalies. We prove that the solution to PRAE is equivalent to the solution of RAE and demonstrate using extensive simulations that PRAE is at par with state-of-the-art methods for anomaly detection.