Stacked SVD or SVD stacked? A Random Matrix Theory perspective on data integration

Modern data analysis increasingly requires identifying shared latent structure across multiple high-dimensional datasets. A commonly used model assumes that the data matrices are noisy observations of low-rank matrices with a shared singular subspace. In this case, two primary methods have emerged for estimating this shared structure, which vary in how they integrate information across datasets. The first approach, termed Stack-SVD, concatenates all the datasets, and then performs a singular value decomposition (SVD). The second approach, termed SVD-Stack, first performs an SVD separately for each dataset, then aggregates the top singular vectors across these datasets, and finally computes a consensus amongst them. While these methods are widely used, they have not been rigorously studied in the proportional asymptotic regime, which is of great practical relevance in today's world of increasing data size and dimensionality. This lack of theoretical understanding has led to uncertainty about which method to choose and limited the ability to fully exploit their potential. To address these challenges, we derive exact expressions for the asymptotic performance and phase transitions of these two methods and develop optimal weighting schemes to further improve both methods. Our analysis reveals that while neither method uniformly dominates the other in the unweighted case, optimally weighted Stack-SVD dominates optimally weighted SVD-Stack. We extend our analysis to accommodate multiple shared components, and provide practical algorithms for estimating optimal weights from data, offering theoretical guidance for method selection in practical data integration problems. Extensive numerical simulations and semi-synthetic experiments on genomic data corroborate our theoretical findings.

OIBench: Benchmarking Strong Reasoning Models with Olympiad in Informatics

As models become increasingly sophisticated, conventional algorithm benchmarks are increasingly saturated, underscoring the need for more challenging benchmarks to guide future improvements in algorithmic reasoning. This paper introduces OIBench, a high-quality, private, and challenging olympiad-level informatics dataset comprising 250 carefully curated original problems. We detail the construction methodology of the benchmark, ensuring a comprehensive assessment across various programming paradigms and complexities, and we demonstrate its contamination-resistant properties via experiments. We propose Time/Space Completion Curves for finer-grained efficiency analysis and enable direct human-model comparisons through high-level participant evaluations. Our experiments reveal that while open-source models lag behind closed-source counterparts, current SOTA models already outperform most human participants in both correctness and efficiency, while still being suboptimal compared to the canonical solutions. By releasing OIBench as a fully open-source resource (https://huggingface.co/datasets/AGI-Eval/OIBench), we hope this benchmark will contribute to advancing code reasoning capabilities for future LLMs.

Optimal Estimation of Shared Singular Subspaces across Multiple Noisy Matrices

Estimating singular subspaces from noisy matrices is a fundamental problem with wide-ranging applications across various fields. Driven by the challenges of data integration and multi-view analysis, this study focuses on estimating shared (left) singular subspaces across multiple matrices within a low-rank matrix denoising framework. A common approach for this task is to perform singular value decomposition on the stacked matrix (Stack-SVD), which is formed by concatenating all the individual matrices. We establish that Stack-SVD achieves minimax rate-optimality when the true (left) singular subspaces of the signal matrices are identical. Our analysis reveals some phase transition phenomena in the estimation problem as a function of the underlying signal-to-noise ratio, highlighting how the interplay among multiple matrices collectively determines the fundamental limits of estimation. We then tackle the more complex scenario where the true singular subspaces are only partially shared across matrices. For various cases of partial sharing, we rigorously characterize the conditions under which Stack-SVD remains effective, achieves minimax optimality, or fails to deliver consistent estimates, offering theoretical insights into its practical applicability. To overcome Stack-SVD's limitations in partial sharing scenarios, we propose novel estimators and an efficient algorithm to identify shared and unshared singular vectors, and prove their minimax rate-optimality. Extensive simulation studies and real-world data applications demonstrate the numerous advantages of our proposed approaches.

Assessing and improving reliability of neighbor embedding methods: a map-continuity perspective

Visualizing high-dimensional data is an important routine for understanding biomedical data and interpreting deep learning models. Neighbor embedding methods, such as t-SNE, UMAP, and LargeVis, among others, are a family of popular visualization methods which reduce high-dimensional data to two dimensions. However, recent studies suggest that these methods often produce visual artifacts, potentially leading to incorrect scientific conclusions. Recognizing that the current limitation stems from a lack of data-independent notions of embedding maps, we introduce a novel conceptual and computational framework, LOO-map, that learns the embedding maps based on a classical statistical idea known as the leave-one-out. LOO-map extends the embedding over a discrete set of input points to the entire input space, enabling a systematic assessment of map continuity, and thus the reliability of the visualizations. We find for many neighbor embedding methods, their embedding maps can be intrinsically discontinuous. The discontinuity induces two types of observed map distortion: ``overconfidence-inducing discontinuity," which exaggerates cluster separation, and ``fracture-inducing discontinuity," which creates spurious local structures. Building upon LOO-map, we propose two diagnostic point-wise scores -- perturbation score and singularity score -- to address these limitations. These scores can help identify unreliable embedding points, detect out-of-distribution data, and guide hyperparameter selection. Our approach is flexible and works as a wrapper around many neighbor embedding algorithms. We test our methods across multiple real-world datasets from computer vision and single-cell omics to demonstrate their effectiveness in enhancing the interpretability and accuracy of visualizations.

Automated Label Unification for Multi-Dataset Semantic Segmentation with GNNs

Deep supervised models possess significant capability to assimilate extensive training data, thereby presenting an opportunity to enhance model performance through training on multiple datasets. However, conflicts arising from different label spaces among datasets may adversely affect model performance. In this paper, we propose a novel approach to automatically construct a unified label space across multiple datasets using graph neural networks. This enables semantic segmentation models to be trained simultaneously on multiple datasets, resulting in performance improvements. Unlike existing methods, our approach facilitates seamless training without the need for additional manual reannotation or taxonomy reconciliation. This significantly enhances the efficiency and effectiveness of multi-dataset segmentation model training. The results demonstrate that our method significantly outperforms other multi-dataset training methods when trained on seven datasets simultaneously, and achieves state-of-the-art performance on the WildDash 2 benchmark.

Entropic Optimal Transport Eigenmaps for Nonlinear Alignment and Joint Embedding of High-Dimensional Datasets

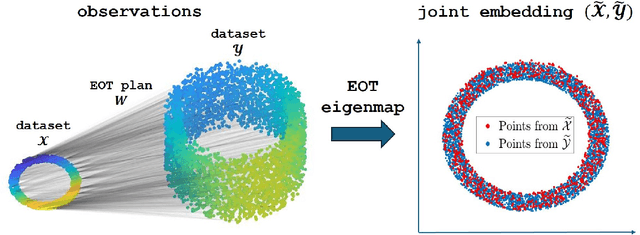
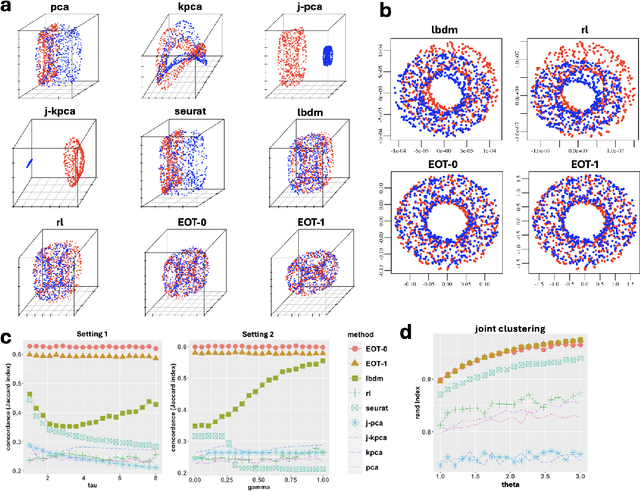
Embedding high-dimensional data into a low-dimensional space is an indispensable component of data analysis. In numerous applications, it is necessary to align and jointly embed multiple datasets from different studies or experimental conditions. Such datasets may share underlying structures of interest but exhibit individual distortions, resulting in misaligned embeddings using traditional techniques. In this work, we propose \textit{Entropic Optimal Transport (EOT) eigenmaps}, a principled approach for aligning and jointly embedding a pair of datasets with theoretical guarantees. Our approach leverages the leading singular vectors of the EOT plan matrix between two datasets to extract their shared underlying structure and align the datasets accordingly in a common embedding space. We interpret our approach as an inter-data variant of the classical Laplacian eigenmaps and diffusion maps embeddings, showing that it enjoys many favorable analogous properties. We then analyze a data-generative model where two observed high-dimensional datasets share latent variables on a common low-dimensional manifold, but each dataset is subject to data-specific translation, scaling, nuisance structures, and noise. We show that in a high-dimensional asymptotic regime, the EOT plan recovers the shared manifold structure by approximating a kernel function evaluated at the locations of the latent variables. Subsequently, we provide a geometric interpretation of our embedding by relating it to the eigenfunctions of population-level operators encoding the density and geometry of the shared manifold. Finally, we showcase the performance of our approach for data integration and embedding through simulations and analyses of real-world biological data, demonstrating its advantages over alternative methods in challenging scenarios.

Sailing in high-dimensional spaces: Low-dimensional embeddings through angle preservation

Low-dimensional embeddings (LDEs) of high-dimensional data are ubiquitous in science and engineering. They allow us to quickly understand the main properties of the data, identify outliers and processing errors, and inform the next steps of data analysis. As such, LDEs have to be faithful to the original high-dimensional data, i.e., they should represent the relationships that are encoded in the data, both at a local as well as global scale. The current generation of LDE approaches focus on reconstructing local distances between any pair of samples correctly, often out-performing traditional approaches aiming at all distances. For these approaches, global relationships are, however, usually strongly distorted, often argued to be an inherent trade-off between local and global structure learning for embeddings. We suggest a new perspective on LDE learning, reconstructing angles between data points. We show that this approach, Mercat, yields good reconstruction across a diverse set of experiments and metrics, and preserve structures well across all scales. Compared to existing work, our approach also has a simple formulation, facilitating future theoretical analysis and algorithmic improvements.

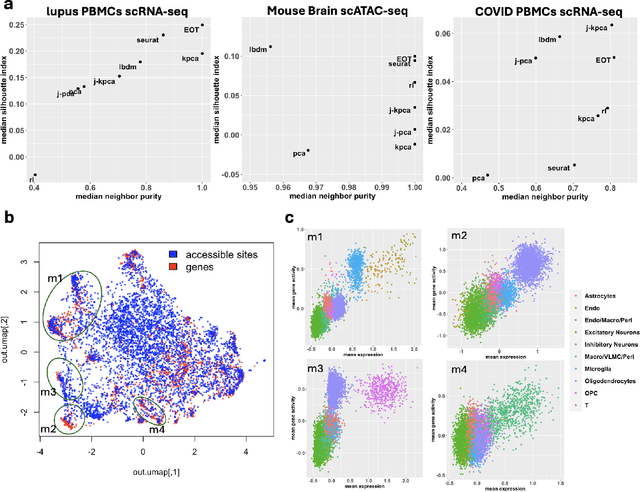
Kernel spectral joint embeddings for high-dimensional noisy datasets using duo-landmark integral operators

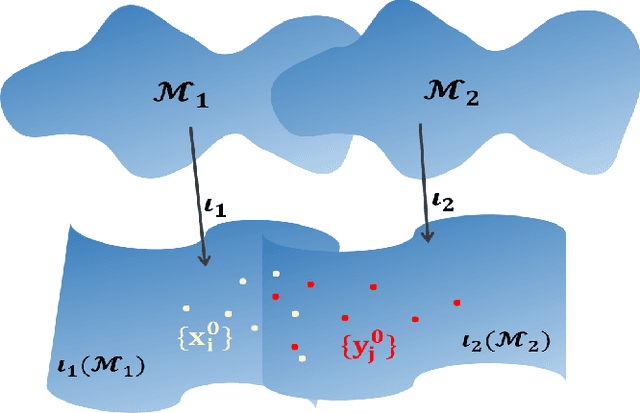
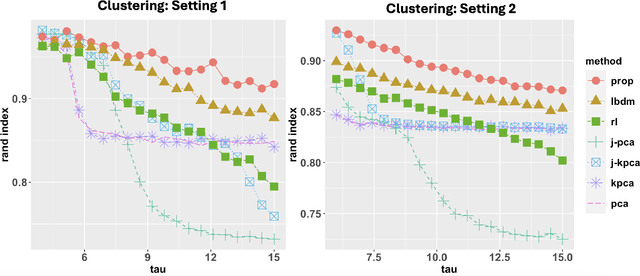
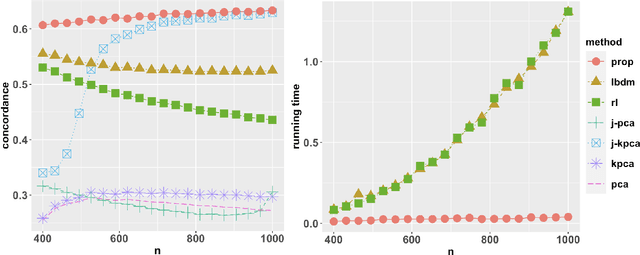
Integrative analysis of multiple heterogeneous datasets has become standard practice in many research fields, especially in single-cell genomics and medical informatics. Existing approaches oftentimes suffer from limited power in capturing nonlinear structures, insufficient account of noisiness and effects of high-dimensionality, lack of adaptivity to signals and sample sizes imbalance, and their results are sometimes difficult to interpret. To address these limitations, we propose a novel kernel spectral method that achieves joint embeddings of two independently observed high-dimensional noisy datasets. The proposed method automatically captures and leverages possibly shared low-dimensional structures across datasets to enhance embedding quality. The obtained low-dimensional embeddings can be utilized for many downstream tasks such as simultaneous clustering, data visualization, and denoising. The proposed method is justified by rigorous theoretical analysis. Specifically, we show the consistency of our method in recovering the low-dimensional noiseless signals, and characterize the effects of the signal-to-noise ratios on the rates of convergence. Under a joint manifolds model framework, we establish the convergence of ultimate embeddings to the eigenfunctions of some newly introduced integral operators. These operators, referred to as duo-landmark integral operators, are defined by the convolutional kernel maps of some reproducing kernel Hilbert spaces (RKHSs). These RKHSs capture the either partially or entirely shared underlying low-dimensional nonlinear signal structures of the two datasets. Our numerical experiments and analyses of two single-cell omics datasets demonstrate the empirical advantages of the proposed method over existing methods in both embeddings and several downstream tasks.

Is your data alignable? Principled and interpretable alignability testing and integration of single-cell data

Single-cell data integration can provide a comprehensive molecular view of cells, and many algorithms have been developed to remove unwanted technical or biological variations and integrate heterogeneous single-cell datasets. Despite their wide usage, existing methods suffer from several fundamental limitations. In particular, we lack a rigorous statistical test for whether two high-dimensional single-cell datasets are alignable (and therefore should even be aligned). Moreover, popular methods can substantially distort the data during alignment, making the aligned data and downstream analysis difficult to interpret. To overcome these limitations, we present a spectral manifold alignment and inference (SMAI) framework, which enables principled and interpretable alignability testing and structure-preserving integration of single-cell data. SMAI provides a statistical test to robustly determine the alignability between datasets to avoid misleading inference, and is justified by high-dimensional statistical theory. On a diverse range of real and simulated benchmark datasets, it outperforms commonly used alignment methods. Moreover, we show that SMAI improves various downstream analyses such as identification of differentially expressed genes and imputation of single-cell spatial transcriptomics, providing further biological insights. SMAI's interpretability also enables quantification and a deeper understanding of the sources of technical confounders in single-cell data.

A Spectral Method for Assessing and Combining Multiple Data Visualizations

Dimension reduction and data visualization aim to project a high-dimensional dataset to a low-dimensional space while capturing the intrinsic structures in the data. It is an indispensable part of modern data science, and many dimensional reduction and visualization algorithms have been developed. However, different algorithms have their own strengths and weaknesses, making it critically important to evaluate their relative performance for a given dataset, and to leverage and combine their individual strengths. In this paper, we propose an efficient spectral method for assessing and combining multiple visualizations of a given dataset produced by diverse algorithms. The proposed method provides a quantitative measure -- the visualization eigenscore -- of the relative performance of the visualizations for preserving the structure around each data point. Then it leverages the eigenscores to obtain a consensus visualization, which has much improved { quality over the individual visualizations in capturing the underlying true data structure.} Our approach is flexible and works as a wrapper around any visualizations. We analyze multiple simulated and real-world datasets from diverse applications to demonstrate the effectiveness of the eigenscores for evaluating visualizations and the superiority of the proposed consensus visualization. Furthermore, we establish rigorous theoretical justification of our method based on a general statistical framework, yielding fundamental principles behind the empirical success of consensus visualization along with practical guidance.