Universality of the $π^2/6$ Pathway in Avoiding Model Collapse

Researchers in empirical machine learning recently spotlighted their fears of so-called Model Collapse. They imagined a discard workflow, where an initial generative model is trained with real data, after which the real data are discarded, and subsequently, the model generates synthetic data on which a new model is trained. They came to the conclusion that models degenerate as model-fitting generations proceed. However, other researchers considered an augment workflow, where the original real data continue to be used in each generation of training, augmented by synthetic data from models fit in all earlier generations. Empirical results on canonical datasets and learning procedures confirmed the occurrence of model collapse under the discard workflow and avoidance of model collapse under the augment workflow. Under the augment workflow, theoretical evidence also confirmed avoidance in particular instances; specifically, Gerstgrasser et al. (2024) found that for classical Linear Regression, test risk at any later generation is bounded by a moderate multiple, viz. pi-squared-over-6 of the test risk of training with the original real data alone. Some commentators questioned the generality of theoretical conclusions based on the generative model assumed in Gerstgrasser et al. (2024): could similar conclusions be reached for other task/model pairings? In this work, we demonstrate the universality of the pi-squared-over-6 augment risk bound across a large family of canonical statistical models, offering key insights into exactly why collapse happens under the discard workflow and is avoided under the augment workflow. In the process, we provide a framework that is able to accommodate a large variety of workflows (beyond discard and augment), thereby enabling an experimenter to judge the comparative merits of multiple different workflows by simulating a simple Gaussian process.

Is your data alignable? Principled and interpretable alignability testing and integration of single-cell data

Single-cell data integration can provide a comprehensive molecular view of cells, and many algorithms have been developed to remove unwanted technical or biological variations and integrate heterogeneous single-cell datasets. Despite their wide usage, existing methods suffer from several fundamental limitations. In particular, we lack a rigorous statistical test for whether two high-dimensional single-cell datasets are alignable (and therefore should even be aligned). Moreover, popular methods can substantially distort the data during alignment, making the aligned data and downstream analysis difficult to interpret. To overcome these limitations, we present a spectral manifold alignment and inference (SMAI) framework, which enables principled and interpretable alignability testing and structure-preserving integration of single-cell data. SMAI provides a statistical test to robustly determine the alignability between datasets to avoid misleading inference, and is justified by high-dimensional statistical theory. On a diverse range of real and simulated benchmark datasets, it outperforms commonly used alignment methods. Moreover, we show that SMAI improves various downstream analyses such as identification of differentially expressed genes and imputation of single-cell spatial transcriptomics, providing further biological insights. SMAI's interpretability also enables quantification and a deeper understanding of the sources of technical confounders in single-cell data.

Convex Sparse Blind Deconvolution

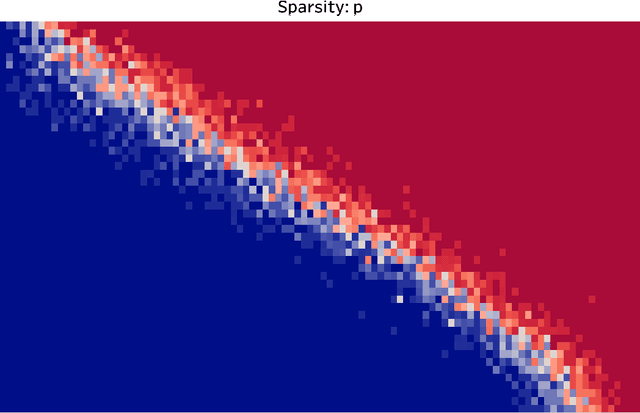
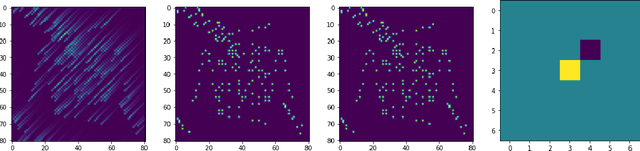
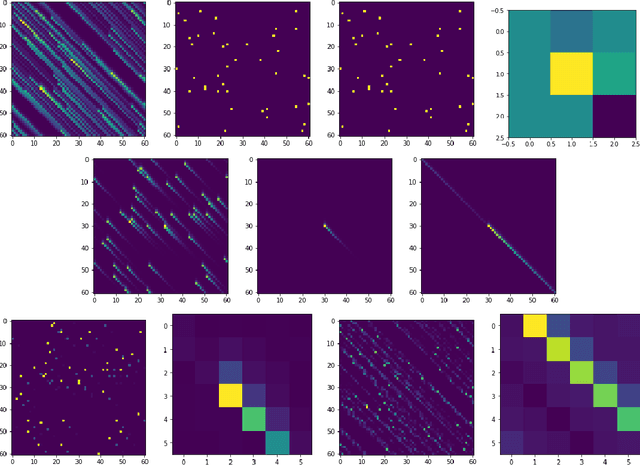
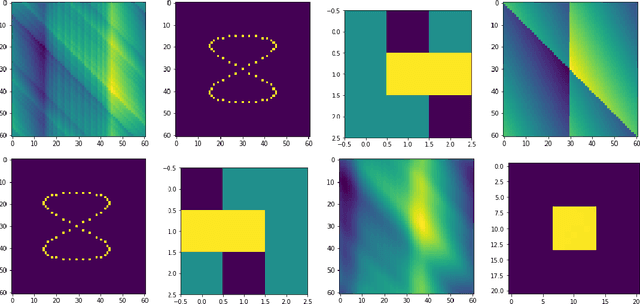
In the blind deconvolution problem, we observe the convolution of an unknown filter and unknown signal and attempt to reconstruct the filter and signal. The problem seems impossible in general, since there are seemingly many more unknowns than knowns . Nevertheless, this problem arises in many application fields; and empirically, some of these fields have had success using heuristic methods -- even economically very important ones, in wireless communications and oil exploration. Today's fashionable heuristic formulations pose non-convex optimization problems which are then attacked heuristically as well. The fact that blind deconvolution can be solved under some repeatable and naturally-occurring circumstances poses a theoretical puzzle. To bridge the gulf between reported successes and theory's limited understanding, we exhibit a convex optimization problem that -- assuming signal sparsity -- can convert a crude approximation to the true filter into a high-accuracy recovery of the true filter. Our proposed formulation is based on L1 minimization of inverse filter outputs. We give sharp guarantees on performance of the minimizer assuming sparsity of signal, showing that our proposal precisely recovers the true inverse filter, up to shift and rescaling. There is a sparsity/initial accuracy tradeoff: the less accurate the initial approximation, the greater we rely on sparsity to enable exact recovery. To our knowledge this is the first reported tradeoff of this kind. We consider it surprising that this tradeoff is independent of dimension. We also develop finite-$N$ guarantees, for highly accurate reconstruction under $N\geq O(k \log(k) )$ with high probability. We further show stable approximation when the true inverse filter is infinitely long and extend our guarantees to the case where the observations are contaminated by stochastic or adversarial noise.

Degrees of Freedom Analysis of Unrolled Neural Networks

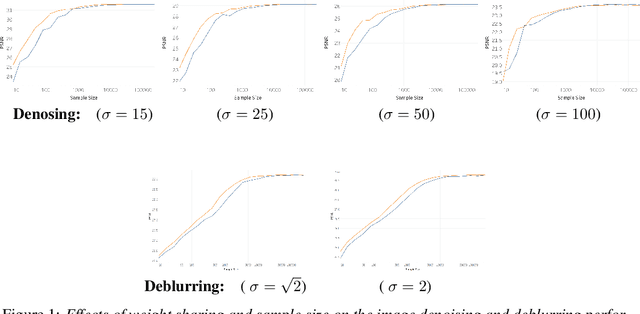
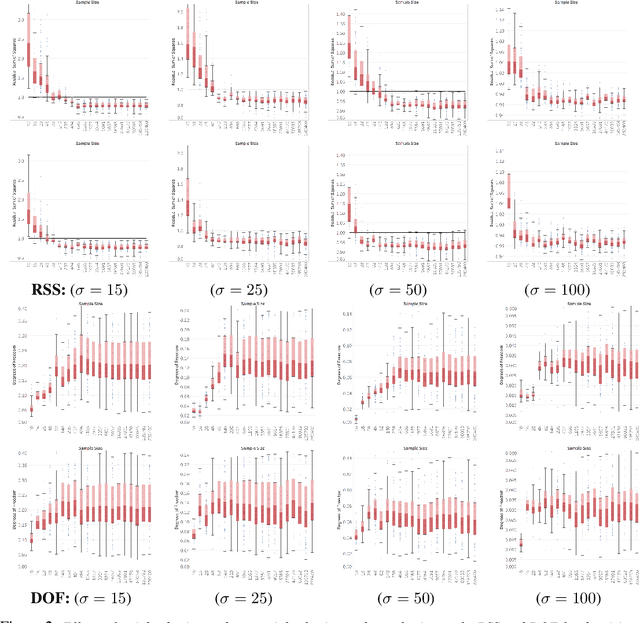
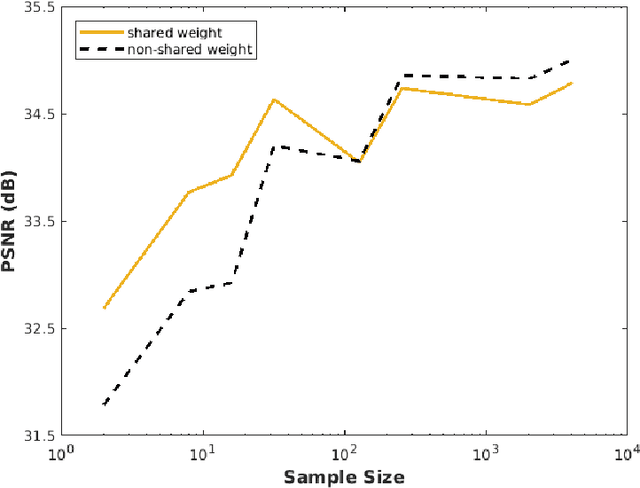
Unrolled neural networks emerged recently as an effective model for learning inverse maps appearing in image restoration tasks. However, their generalization risk (i.e., test mean-squared-error) and its link to network design and train sample size remains mysterious. Leveraging the Stein's Unbiased Risk Estimator (SURE), this paper analyzes the generalization risk with its bias and variance components for recurrent unrolled networks. We particularly investigate the degrees-of-freedom (DOF) component of SURE, trace of the end-to-end network Jacobian, to quantify the prediction variance. We prove that DOF is well-approximated by the weighted \textit{path sparsity} of the network under incoherence conditions on the trained weights. Empirically, we examine the SURE components as a function of train sample size for both recurrent and non-recurrent (with many more parameters) unrolled networks. Our key observations indicate that: 1) DOF increases with train sample size and converges to the generalization risk for both recurrent and non-recurrent schemes; 2) recurrent network converges significantly faster (with less train samples) compared with non-recurrent scheme, hence recurrence serves as a regularization for low sample size regimes.

Neural Proximal Gradient Descent for Compressive Imaging

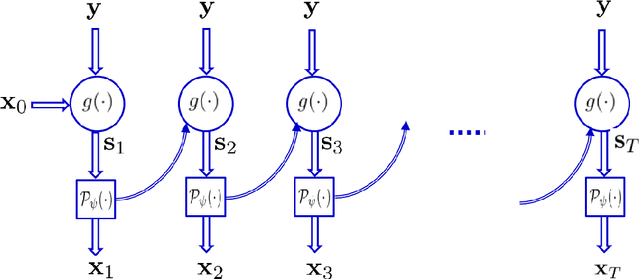
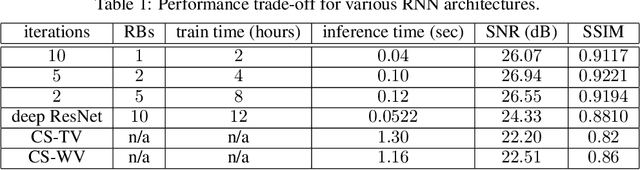
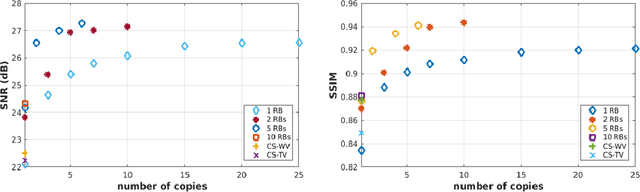
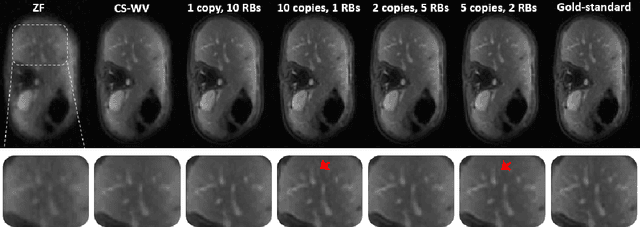
Recovering high-resolution images from limited sensory data typically leads to a serious ill-posed inverse problem, demanding inversion algorithms that effectively capture the prior information. Learning a good inverse mapping from training data faces severe challenges, including: (i) scarcity of training data; (ii) need for plausible reconstructions that are physically feasible; (iii) need for fast reconstruction, especially in real-time applications. We develop a successful system solving all these challenges, using as basic architecture the recurrent application of proximal gradient algorithm. We learn a proximal map that works well with real images based on residual networks. Contraction of the resulting map is analyzed, and incoherence conditions are investigated that drive the convergence of the iterates. Extensive experiments are carried out under different settings: (a) reconstructing abdominal MRI of pediatric patients from highly undersampled Fourier-space data and (b) superresolving natural face images. Our key findings include: 1. a recurrent ResNet with a single residual block unrolled from an iterative algorithm yields an effective proximal which accurately reveals MR image details. 2. Our architecture significantly outperforms conventional non-recurrent deep ResNets by 2dB SNR; it is also trained much more rapidly. 3. It outperforms state-of-the-art compressed-sensing Wavelet-based methods by 4dB SNR, with 100x speedups in reconstruction time.

Recurrent Generative Adversarial Networks for Proximal Learning and Automated Compressive Image Recovery

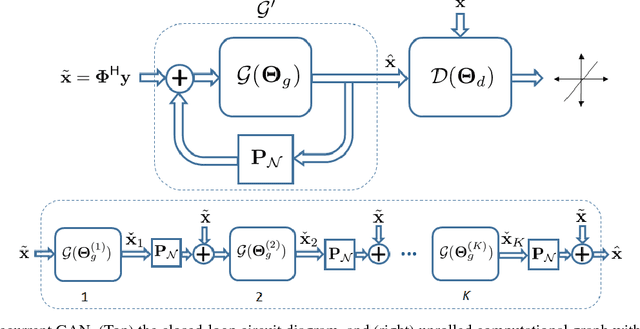
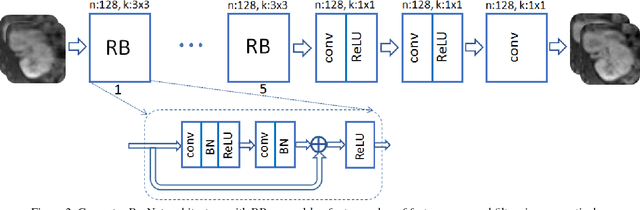
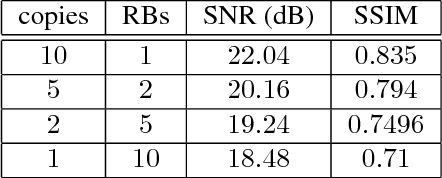
Recovering images from undersampled linear measurements typically leads to an ill-posed linear inverse problem, that asks for proper statistical priors. Building effective priors is however challenged by the low train and test overhead dictated by real-time tasks; and the need for retrieving visually "plausible" and physically "feasible" images with minimal hallucination. To cope with these challenges, we design a cascaded network architecture that unrolls the proximal gradient iterations by permeating benefits from generative residual networks (ResNet) to modeling the proximal operator. A mixture of pixel-wise and perceptual costs is then deployed to train proximals. The overall architecture resembles back-and-forth projection onto the intersection of feasible and plausible images. Extensive computational experiments are examined for a global task of reconstructing MR images of pediatric patients, and a more local task of superresolving CelebA faces, that are insightful to design efficient architectures. Our observations indicate that for MRI reconstruction, a recurrent ResNet with a single residual block effectively learns the proximal. This simple architecture appears to significantly outperform the alternative deep ResNet architecture by 2dB SNR, and the conventional compressed-sensing MRI by 4dB SNR with 100x faster inference. For image superresolution, our preliminary results indicate that modeling the denoising proximal demands deep ResNets.