Optimal Vector Compressed Sensing Using James Stein Shrinkage

The trend in modern science and technology is to take vector measurements rather than scalars, ruthlessly scaling to ever higher dimensional vectors. For about two decades now, traditional scalar Compressed Sensing has been synonymous with a Convex Optimization based procedure called Basis Pursuit. In the vector recovery case, the natural tendency is to return to a straightforward vector extension of Basis Pursuit, also based on Convex Optimization. However, Convex Optimization is provably suboptimal, particularly when $B$ is large. In this paper, we propose SteinSense, a lightweight iterative algorithm, which is provably optimal when $B$ is large. It does not have any tuning parameter, does not need any training data, requires zero knowledge of sparsity, is embarrassingly simple to implement, and all of this makes it easily scalable to high vector dimensions. We conduct a massive volume of both real and synthetic experiments that confirm the efficacy of SteinSense, and also provide theoretical justification based on ideas from Approximate Message Passing. Fascinatingly, we discover that SteinSense is quite robust, delivering the same quality of performance on real data, and even under substantial departures from conditions under which existing theory holds.

Universality of the $π^2/6$ Pathway in Avoiding Model Collapse

Researchers in empirical machine learning recently spotlighted their fears of so-called Model Collapse. They imagined a discard workflow, where an initial generative model is trained with real data, after which the real data are discarded, and subsequently, the model generates synthetic data on which a new model is trained. They came to the conclusion that models degenerate as model-fitting generations proceed. However, other researchers considered an augment workflow, where the original real data continue to be used in each generation of training, augmented by synthetic data from models fit in all earlier generations. Empirical results on canonical datasets and learning procedures confirmed the occurrence of model collapse under the discard workflow and avoidance of model collapse under the augment workflow. Under the augment workflow, theoretical evidence also confirmed avoidance in particular instances; specifically, Gerstgrasser et al. (2024) found that for classical Linear Regression, test risk at any later generation is bounded by a moderate multiple, viz. pi-squared-over-6 of the test risk of training with the original real data alone. Some commentators questioned the generality of theoretical conclusions based on the generative model assumed in Gerstgrasser et al. (2024): could similar conclusions be reached for other task/model pairings? In this work, we demonstrate the universality of the pi-squared-over-6 augment risk bound across a large family of canonical statistical models, offering key insights into exactly why collapse happens under the discard workflow and is avoided under the augment workflow. In the process, we provide a framework that is able to accommodate a large variety of workflows (beyond discard and augment), thereby enabling an experimenter to judge the comparative merits of multiple different workflows by simulating a simple Gaussian process.

Collapse or Thrive? Perils and Promises of Synthetic Data in a Self-Generating World

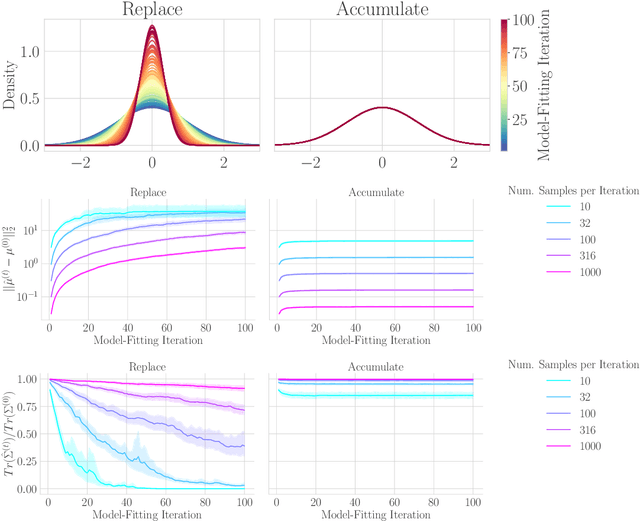
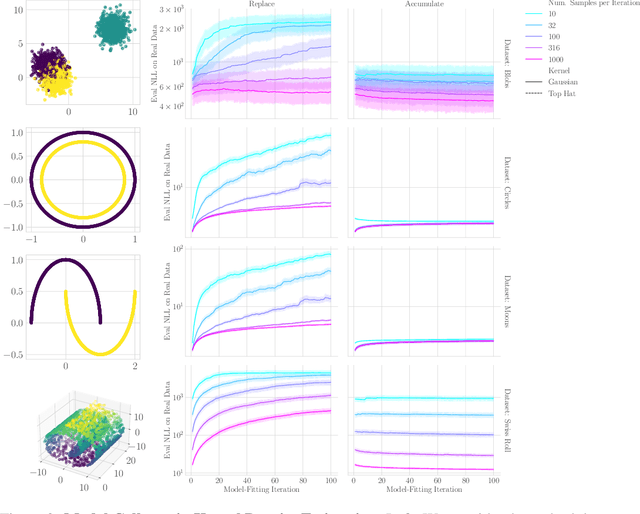
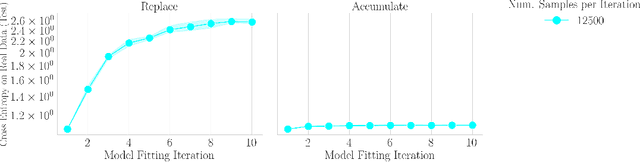
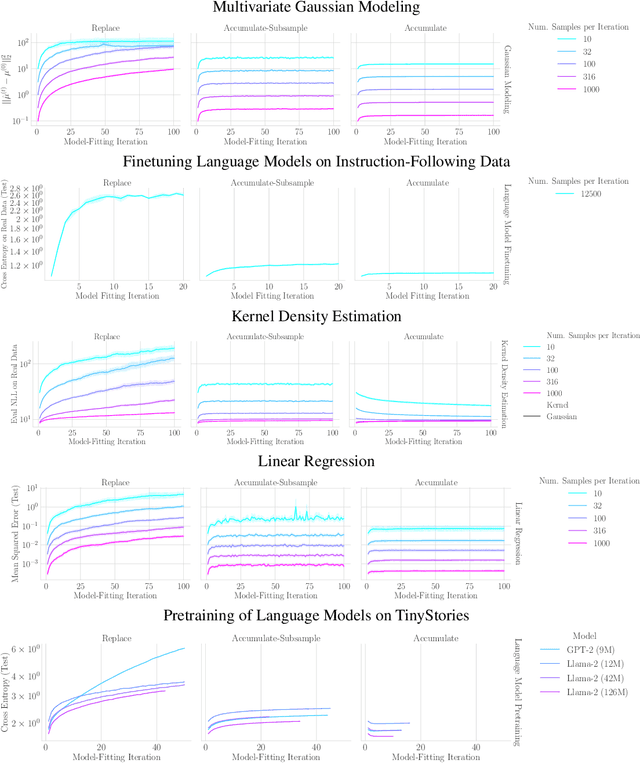
The increasing presence of AI-generated content on the internet raises a critical question: What happens when generative machine learning models are pretrained on web-scale datasets containing data created by earlier models? Some authors prophesy $\textit{model collapse}$ under a "$\textit{replace}$" scenario: a sequence of models, the first trained with real data and each later one trained only on synthetic data from its preceding model. In this scenario, models successively degrade. Others see collapse as easily avoidable; in an "$\textit{accumulate}$' scenario, a sequence of models is trained, but each training uses all real and synthetic data generated so far. In this work, we deepen and extend the study of these contrasting scenarios. First, collapse versus avoidance of collapse is studied by comparing the replace and accumulate scenarios on each of three prominent generative modeling settings; we find the same contrast emerges in all three settings. Second, we study a compromise scenario; the available data remains the same as in the accumulate scenario -- but unlike $\textit{accumulate}$ and like $\textit{replace}$, each model is trained using a fixed compute budget; we demonstrate that model test loss on real data is larger than in the $\textit{accumulate}$ scenario, but apparently plateaus, unlike the divergence seen with $\textit{replace}$. Third, we study the relative importance of cardinality and proportion of real data for avoiding model collapse. Surprisingly, we find a non-trivial interaction between real and synthetic data, where the value of synthetic data for reducing test loss depends on the absolute quantity of real data. Our insights are particularly important when forecasting whether future frontier generative models will collapse or thrive, and our results open avenues for empirically and mathematically studying the context-dependent value of synthetic data.

Is Model Collapse Inevitable? Breaking the Curse of Recursion by Accumulating Real and Synthetic Data

The proliferation of generative models, combined with pretraining on web-scale data, raises a timely question: what happens when these models are trained on their own generated outputs? Recent investigations into model-data feedback loops discovered that such loops can lead to model collapse, a phenomenon where performance progressively degrades with each model-fitting iteration until the latest model becomes useless. However, several recent papers studying model collapse assumed that new data replace old data over time rather than assuming data accumulate over time. In this paper, we compare these two settings and show that accumulating data prevents model collapse. We begin by studying an analytically tractable setup in which a sequence of linear models are fit to the previous models' predictions. Previous work showed if data are replaced, the test error increases linearly with the number of model-fitting iterations; we extend this result by proving that if data instead accumulate, the test error has a finite upper bound independent of the number of iterations. We next empirically test whether accumulating data similarly prevents model collapse by pretraining sequences of language models on text corpora. We confirm that replacing data does indeed cause model collapse, then demonstrate that accumulating data prevents model collapse; these results hold across a range of model sizes, architectures and hyperparameters. We further show that similar results hold for other deep generative models on real data: diffusion models for molecule generation and variational autoencoders for image generation. Our work provides consistent theoretical and empirical evidence that data accumulation mitigates model collapse.