Collapse or Thrive? Perils and Promises of Synthetic Data in a Self-Generating World

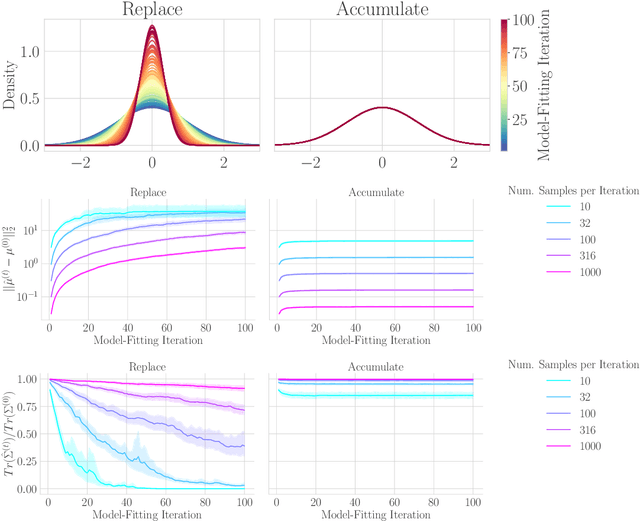
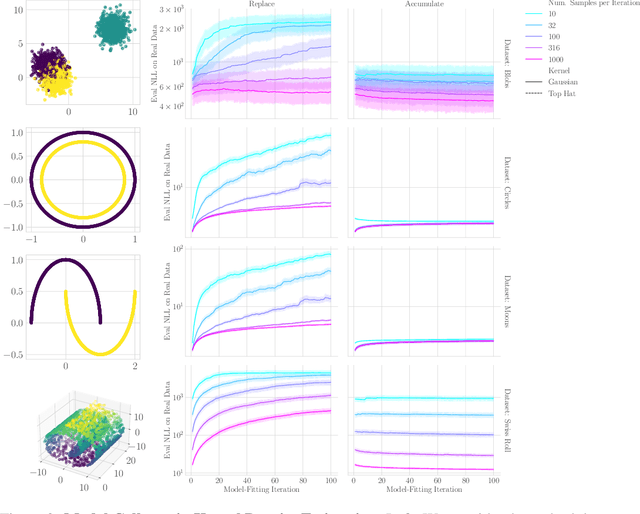
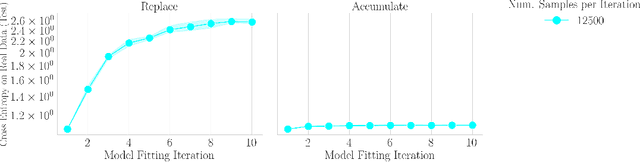
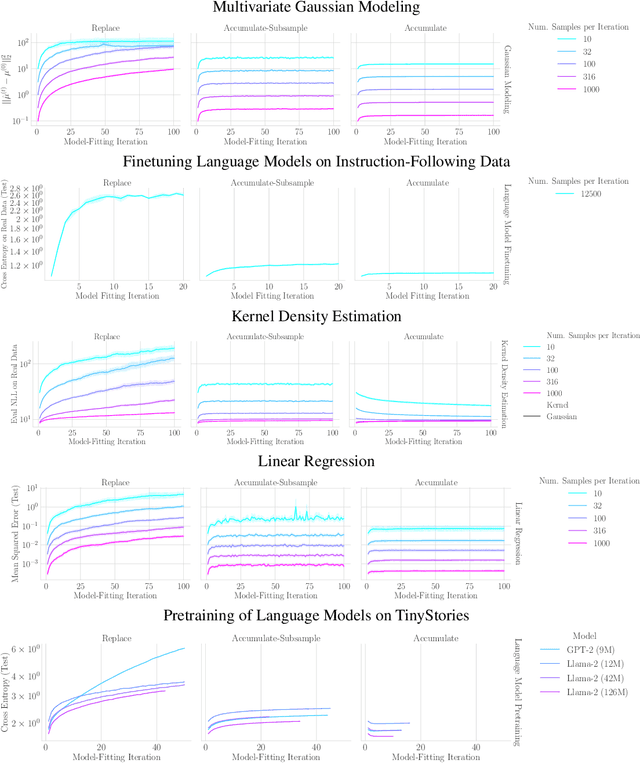
The increasing presence of AI-generated content on the internet raises a critical question: What happens when generative machine learning models are pretrained on web-scale datasets containing data created by earlier models? Some authors prophesy $\textit{model collapse}$ under a "$\textit{replace}$" scenario: a sequence of models, the first trained with real data and each later one trained only on synthetic data from its preceding model. In this scenario, models successively degrade. Others see collapse as easily avoidable; in an "$\textit{accumulate}$' scenario, a sequence of models is trained, but each training uses all real and synthetic data generated so far. In this work, we deepen and extend the study of these contrasting scenarios. First, collapse versus avoidance of collapse is studied by comparing the replace and accumulate scenarios on each of three prominent generative modeling settings; we find the same contrast emerges in all three settings. Second, we study a compromise scenario; the available data remains the same as in the accumulate scenario -- but unlike $\textit{accumulate}$ and like $\textit{replace}$, each model is trained using a fixed compute budget; we demonstrate that model test loss on real data is larger than in the $\textit{accumulate}$ scenario, but apparently plateaus, unlike the divergence seen with $\textit{replace}$. Third, we study the relative importance of cardinality and proportion of real data for avoiding model collapse. Surprisingly, we find a non-trivial interaction between real and synthetic data, where the value of synthetic data for reducing test loss depends on the absolute quantity of real data. Our insights are particularly important when forecasting whether future frontier generative models will collapse or thrive, and our results open avenues for empirically and mathematically studying the context-dependent value of synthetic data.

Is Model Collapse Inevitable? Breaking the Curse of Recursion by Accumulating Real and Synthetic Data

The proliferation of generative models, combined with pretraining on web-scale data, raises a timely question: what happens when these models are trained on their own generated outputs? Recent investigations into model-data feedback loops discovered that such loops can lead to model collapse, a phenomenon where performance progressively degrades with each model-fitting iteration until the latest model becomes useless. However, several recent papers studying model collapse assumed that new data replace old data over time rather than assuming data accumulate over time. In this paper, we compare these two settings and show that accumulating data prevents model collapse. We begin by studying an analytically tractable setup in which a sequence of linear models are fit to the previous models' predictions. Previous work showed if data are replaced, the test error increases linearly with the number of model-fitting iterations; we extend this result by proving that if data instead accumulate, the test error has a finite upper bound independent of the number of iterations. We next empirically test whether accumulating data similarly prevents model collapse by pretraining sequences of language models on text corpora. We confirm that replacing data does indeed cause model collapse, then demonstrate that accumulating data prevents model collapse; these results hold across a range of model sizes, architectures and hyperparameters. We further show that similar results hold for other deep generative models on real data: diffusion models for molecule generation and variational autoencoders for image generation. Our work provides consistent theoretical and empirical evidence that data accumulation mitigates model collapse.

Neural Collapse Under MSE Loss: Proximity to and Dynamics on the Central Path

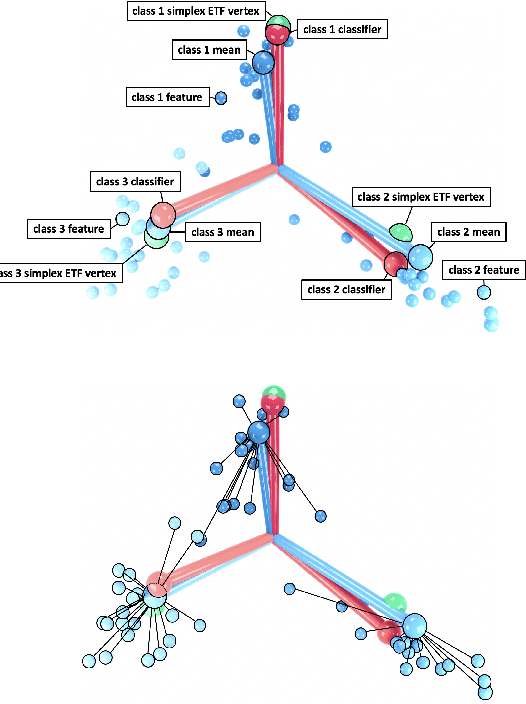
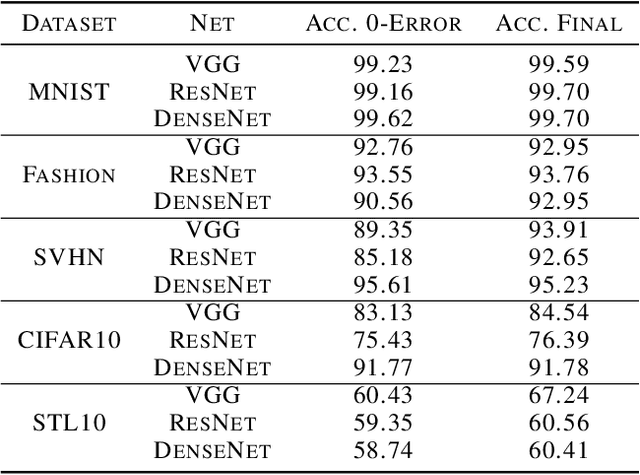
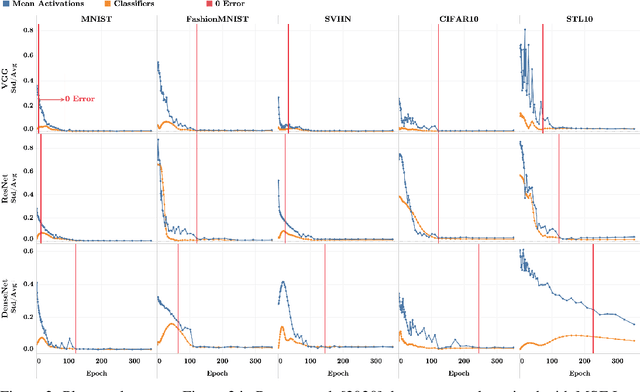
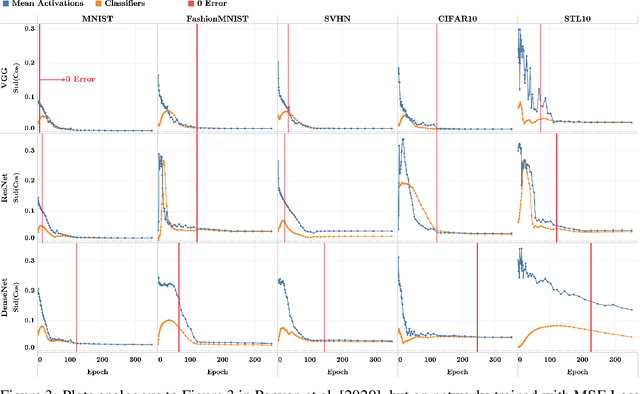
Recent work [Papyan, Han, and Donoho, 2020] discovered a phenomenon called Neural Collapse (NC) that occurs pervasively in today's deep net training paradigm of driving cross-entropy loss towards zero. In this phenomenon, the last-layer features collapse to their class-means, both the classifiers and class-means collapse to the same Simplex Equiangular Tight Frame (ETF), and the behavior of the last-layer classifier converges to that of the nearest-class-mean decision rule. Since then, follow-ups-such as Mixon et al. [2020] and Poggio and Liao [2020a,b]-formally analyzed this inductive bias by replacing the hard-to-study cross-entropy by the more tractable mean squared error (MSE) loss. But, these works stopped short of demonstrating the empirical reality of MSE-NC on benchmark datasets and canonical networks-as had been done in Papyan, Han, and Donoho [2020] for the cross-entropy loss. In this work, we establish the empirical reality of MSE-NC by reporting experimental observations for three prototypical networks and five canonical datasets with code for reproducing NC. Following this, we develop three main contributions inspired by MSE-NC. Firstly, we show a new theoretical decomposition of the MSE loss into (A) a term assuming the last-layer classifier is exactly the least-squares or Webb and Lowe [1990] classifier and (B) a term capturing the deviation from this least-squares classifier. Secondly, we exhibit experiments on canonical datasets and networks demonstrating that, during training, term-(B) is negligible. This motivates a new theoretical construct: the central path, where the linear classifier stays MSE-optimal-for the given feature activations-throughout the dynamics. Finally, through our study of continually renormalized gradient flow along the central path, we produce closed-form dynamics that predict full Neural Collapse in an unconstrained features model.

Prevalence of Neural Collapse during the terminal phase of deep learning training

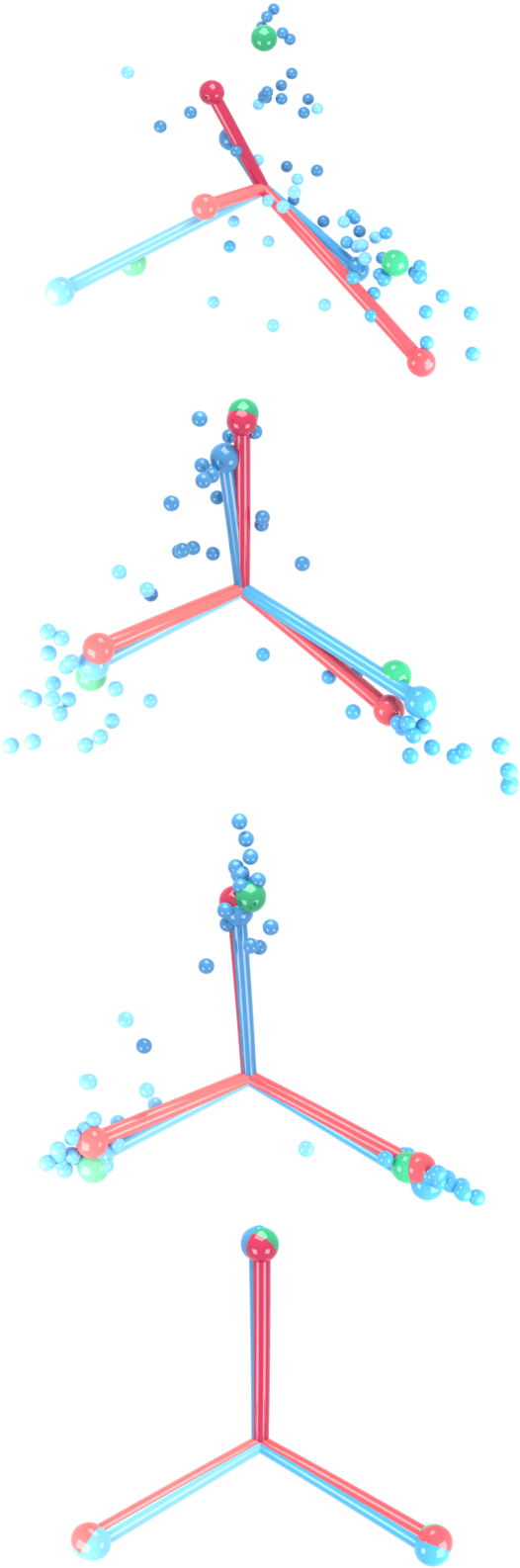
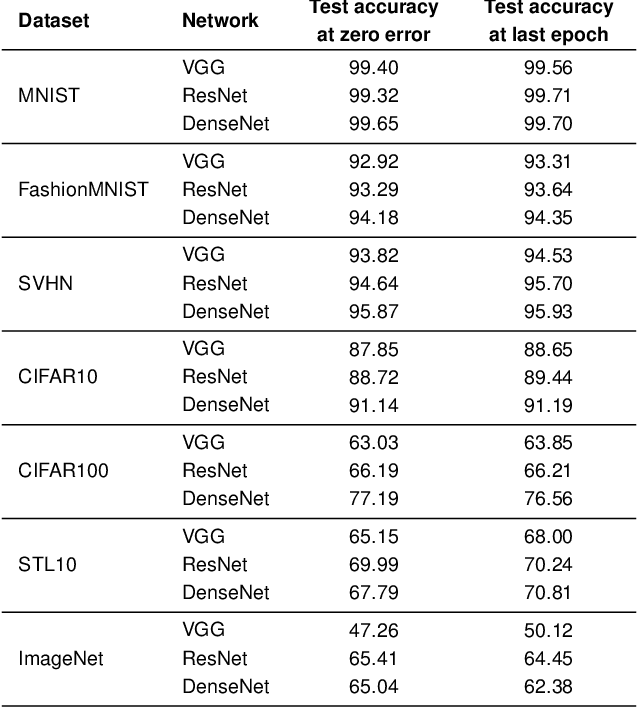
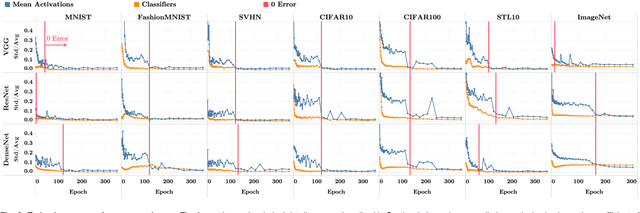
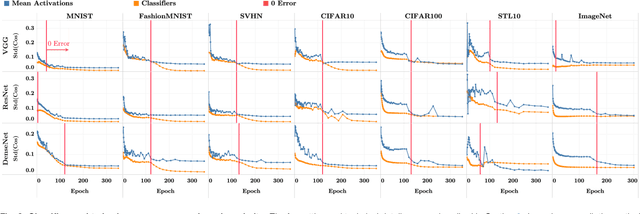
Modern practice for training classification deepnets involves a Terminal Phase of Training (TPT), which begins at the epoch where training error first vanishes; During TPT, the training error stays effectively zero while training loss is pushed towards zero. Direct measurements of TPT, for three prototypical deepnet architectures and across seven canonical classification datasets, expose a pervasive inductive bias we call Neural Collapse, involving four deeply interconnected phenomena: (NC1) Cross-example within-class variability of last-layer training activations collapses to zero, as the individual activations themselves collapse to their class-means; (NC2) The class-means collapse to the vertices of a Simplex Equiangular Tight Frame (ETF); (NC3) Up to rescaling, the last-layer classifiers collapse to the class-means, or in other words to the Simplex ETF, i.e. to a self-dual configuration; (NC4) For a given activation, the classifier's decision collapses to simply choosing whichever class has the closest train class-mean, i.e. the Nearest Class Center (NCC) decision rule. The symmetric and very simple geometry induced by the TPT confers important benefits, including better generalization performance, better robustness, and better interpretability.