Neural Collapse Under MSE Loss: Proximity to and Dynamics on the Central Path
Paper and Code
Jun 03, 2021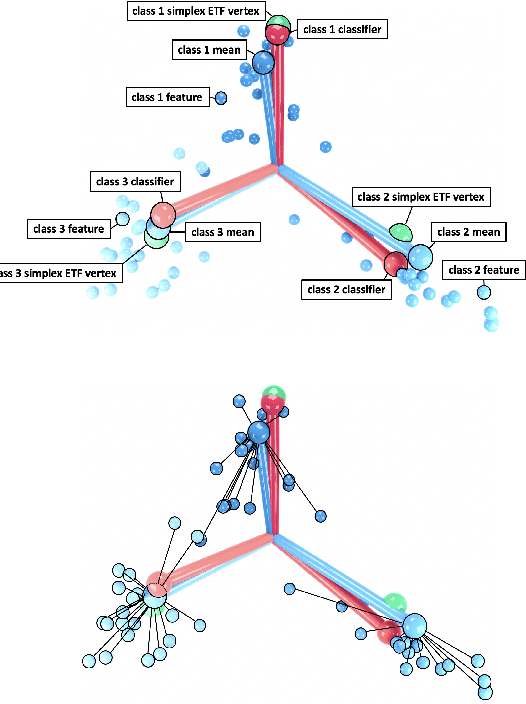
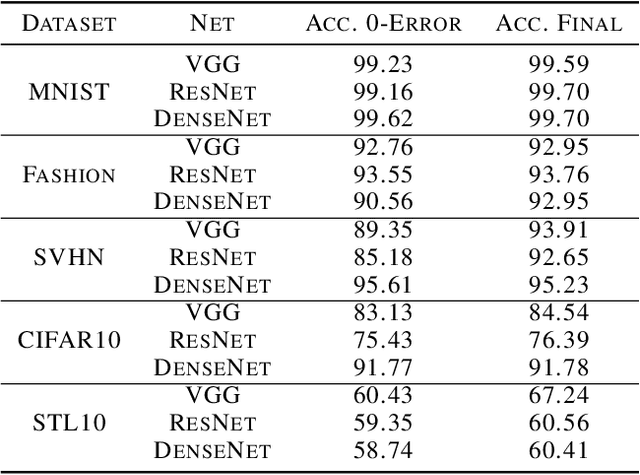
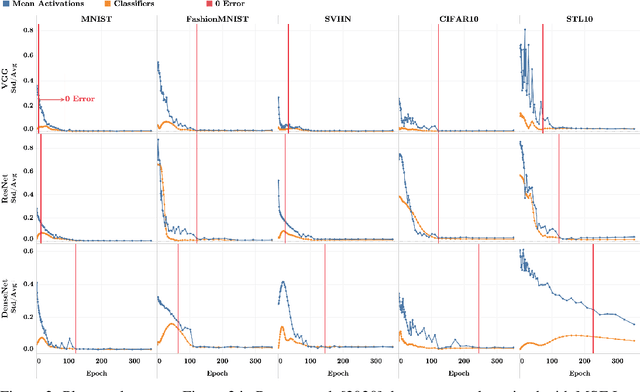
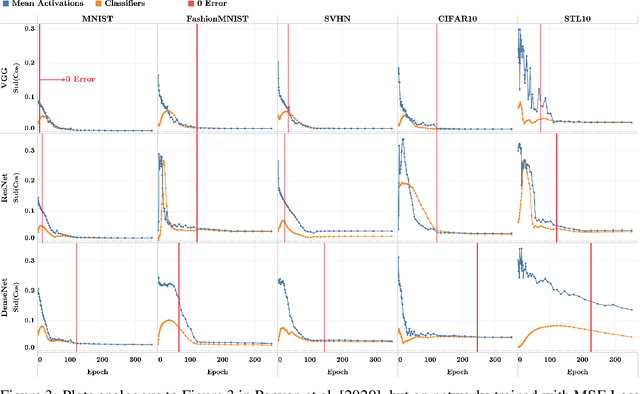
Recent work [Papyan, Han, and Donoho, 2020] discovered a phenomenon called Neural Collapse (NC) that occurs pervasively in today's deep net training paradigm of driving cross-entropy loss towards zero. In this phenomenon, the last-layer features collapse to their class-means, both the classifiers and class-means collapse to the same Simplex Equiangular Tight Frame (ETF), and the behavior of the last-layer classifier converges to that of the nearest-class-mean decision rule. Since then, follow-ups-such as Mixon et al. [2020] and Poggio and Liao [2020a,b]-formally analyzed this inductive bias by replacing the hard-to-study cross-entropy by the more tractable mean squared error (MSE) loss. But, these works stopped short of demonstrating the empirical reality of MSE-NC on benchmark datasets and canonical networks-as had been done in Papyan, Han, and Donoho [2020] for the cross-entropy loss. In this work, we establish the empirical reality of MSE-NC by reporting experimental observations for three prototypical networks and five canonical datasets with code for reproducing NC. Following this, we develop three main contributions inspired by MSE-NC. Firstly, we show a new theoretical decomposition of the MSE loss into (A) a term assuming the last-layer classifier is exactly the least-squares or Webb and Lowe [1990] classifier and (B) a term capturing the deviation from this least-squares classifier. Secondly, we exhibit experiments on canonical datasets and networks demonstrating that, during training, term-(B) is negligible. This motivates a new theoretical construct: the central path, where the linear classifier stays MSE-optimal-for the given feature activations-throughout the dynamics. Finally, through our study of continually renormalized gradient flow along the central path, we produce closed-form dynamics that predict full Neural Collapse in an unconstrained features model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge