Survey Descent: A Multipoint Generalization of Gradient Descent for Nonsmooth Optimization

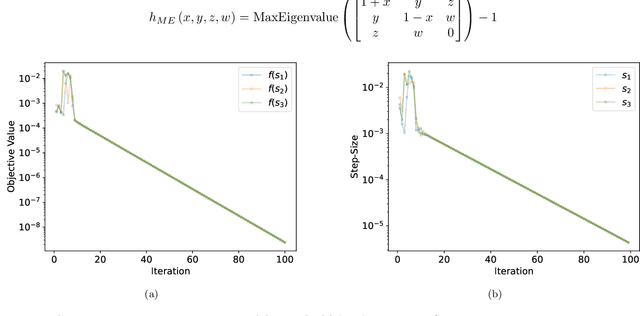
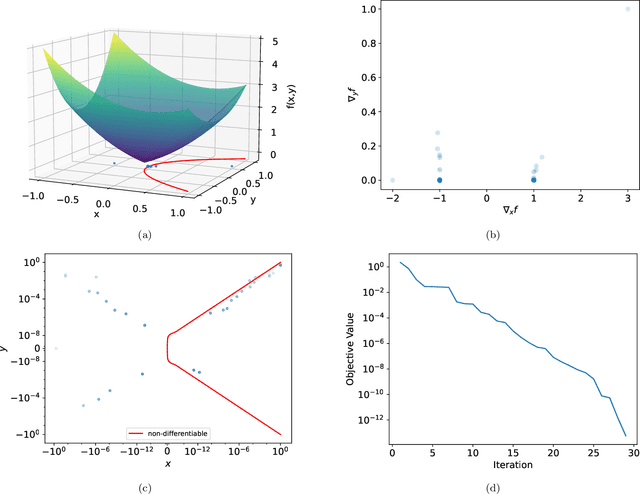
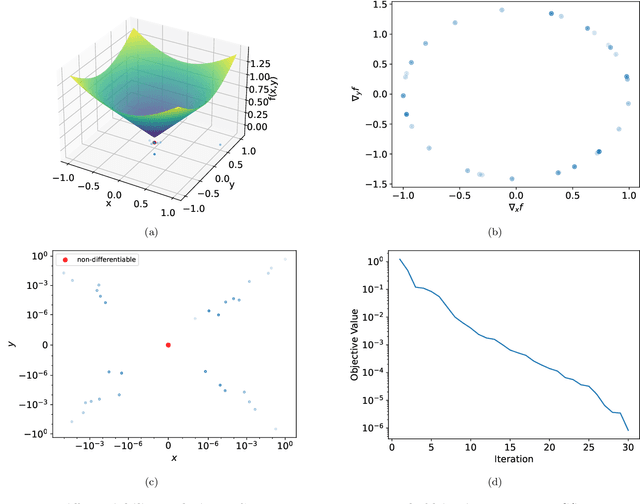
For strongly convex objectives that are smooth, the classical theory of gradient descent ensures linear convergence relative to the number of gradient evaluations. An analogous nonsmooth theory is challenging: even when the objective is smooth at every iterate, the corresponding local models are unstable, and traditional remedies need unpredictably many cutting planes. We instead propose a multipoint generalization of the gradient descent iteration for local optimization. While designed with general objectives in mind, we are motivated by a "max-of-smooth" model that captures subdifferential dimension at optimality. We prove linear convergence when the objective is itself max-of-smooth, and experiments suggest a more general phenomenon.

Neural Collapse Under MSE Loss: Proximity to and Dynamics on the Central Path

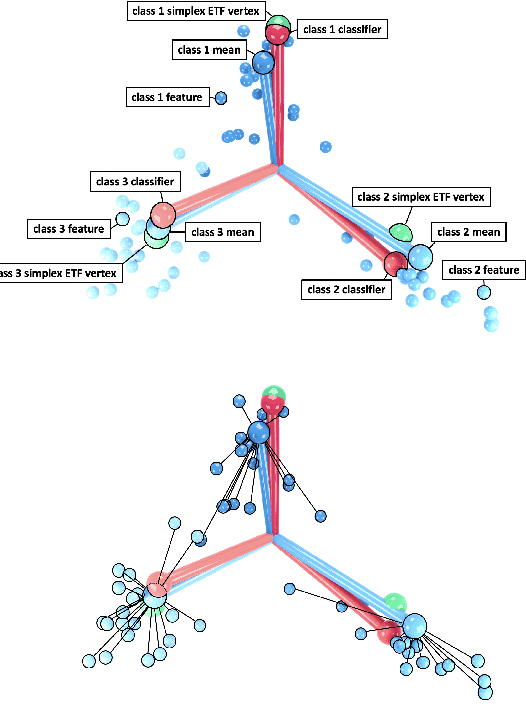
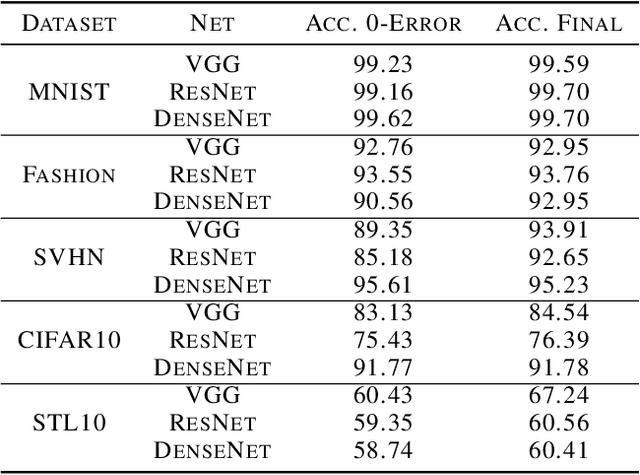
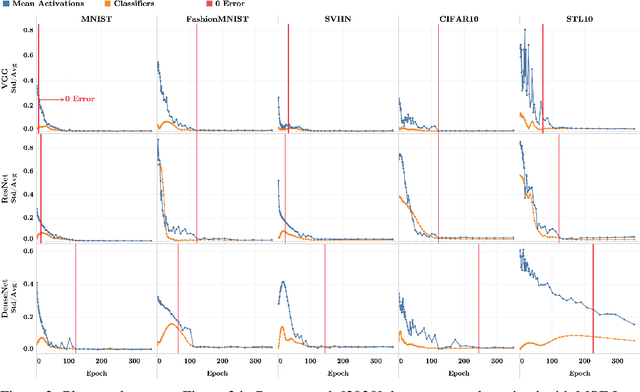
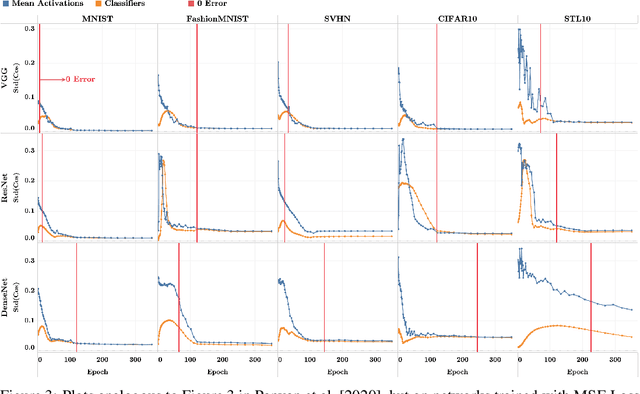
Recent work [Papyan, Han, and Donoho, 2020] discovered a phenomenon called Neural Collapse (NC) that occurs pervasively in today's deep net training paradigm of driving cross-entropy loss towards zero. In this phenomenon, the last-layer features collapse to their class-means, both the classifiers and class-means collapse to the same Simplex Equiangular Tight Frame (ETF), and the behavior of the last-layer classifier converges to that of the nearest-class-mean decision rule. Since then, follow-ups-such as Mixon et al. [2020] and Poggio and Liao [2020a,b]-formally analyzed this inductive bias by replacing the hard-to-study cross-entropy by the more tractable mean squared error (MSE) loss. But, these works stopped short of demonstrating the empirical reality of MSE-NC on benchmark datasets and canonical networks-as had been done in Papyan, Han, and Donoho [2020] for the cross-entropy loss. In this work, we establish the empirical reality of MSE-NC by reporting experimental observations for three prototypical networks and five canonical datasets with code for reproducing NC. Following this, we develop three main contributions inspired by MSE-NC. Firstly, we show a new theoretical decomposition of the MSE loss into (A) a term assuming the last-layer classifier is exactly the least-squares or Webb and Lowe [1990] classifier and (B) a term capturing the deviation from this least-squares classifier. Secondly, we exhibit experiments on canonical datasets and networks demonstrating that, during training, term-(B) is negligible. This motivates a new theoretical construct: the central path, where the linear classifier stays MSE-optimal-for the given feature activations-throughout the dynamics. Finally, through our study of continually renormalized gradient flow along the central path, we produce closed-form dynamics that predict full Neural Collapse in an unconstrained features model.

Prevalence of Neural Collapse during the terminal phase of deep learning training

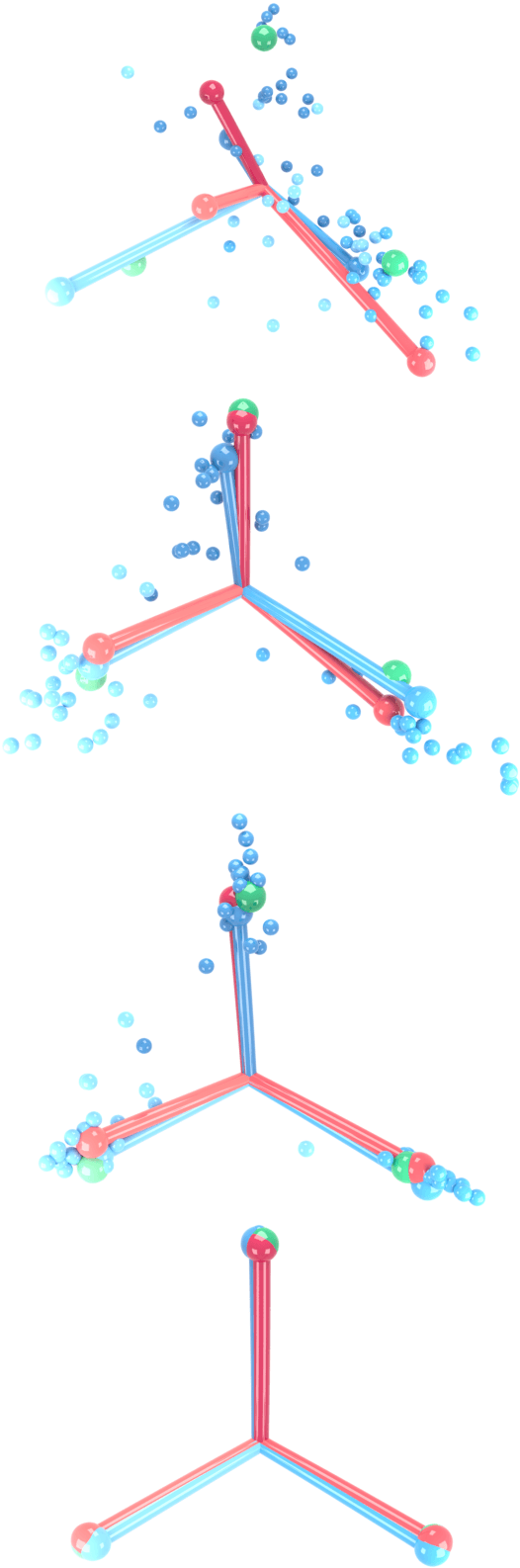
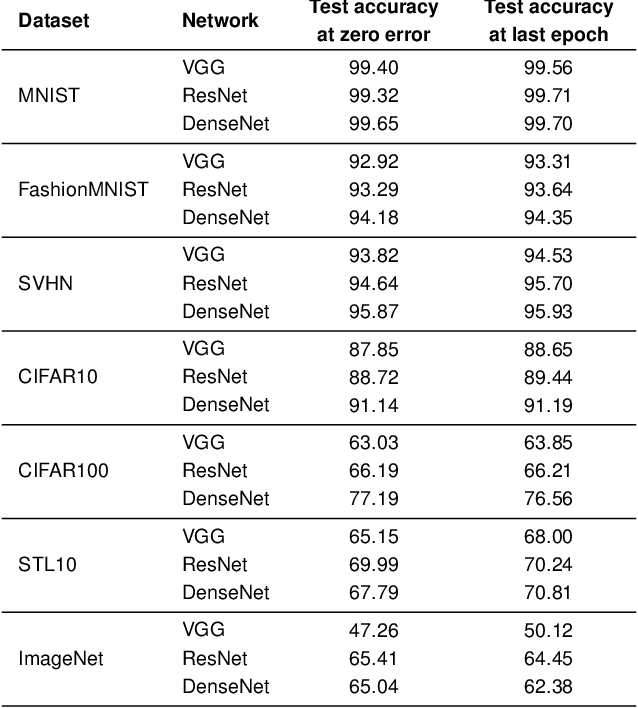
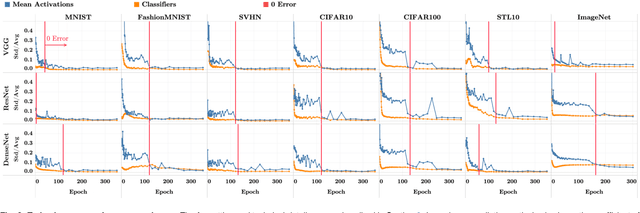
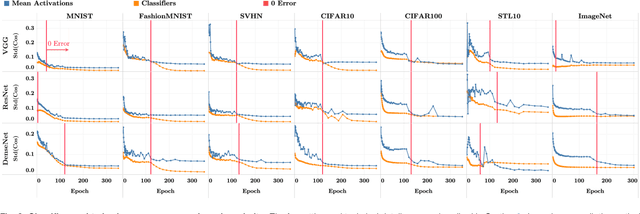
Modern practice for training classification deepnets involves a Terminal Phase of Training (TPT), which begins at the epoch where training error first vanishes; During TPT, the training error stays effectively zero while training loss is pushed towards zero. Direct measurements of TPT, for three prototypical deepnet architectures and across seven canonical classification datasets, expose a pervasive inductive bias we call Neural Collapse, involving four deeply interconnected phenomena: (NC1) Cross-example within-class variability of last-layer training activations collapses to zero, as the individual activations themselves collapse to their class-means; (NC2) The class-means collapse to the vertices of a Simplex Equiangular Tight Frame (ETF); (NC3) Up to rescaling, the last-layer classifiers collapse to the class-means, or in other words to the Simplex ETF, i.e. to a self-dual configuration; (NC4) For a given activation, the classifier's decision collapses to simply choosing whichever class has the closest train class-mean, i.e. the Nearest Class Center (NCC) decision rule. The symmetric and very simple geometry induced by the TPT confers important benefits, including better generalization performance, better robustness, and better interpretability.