On the Importance of Gaussianizing Representations

The normal distribution plays a central role in information theory - it is at the same time the best-case signal and worst-case noise distribution, has the greatest representational capacity of any distribution, and offers an equivalence between uncorrelatedness and independence for joint distributions. Accounting for the mean and variance of activations throughout the layers of deep neural networks has had a significant effect on facilitating their effective training, but seldom has a prescription for precisely what distribution these activations should take, and how this might be achieved, been offered. Motivated by the information-theoretic properties of the normal distribution, we address this question and concurrently present normality normalization: a novel normalization layer which encourages normality in the feature representations of neural networks using the power transform and employs additive Gaussian noise during training. Our experiments comprehensively demonstrate the effectiveness of normality normalization, in regards to its generalization performance on an array of widely used model and dataset combinations, its strong performance across various common factors of variation such as model width, depth, and training minibatch size, its suitability for usage wherever existing normalization layers are conventionally used, and as a means to improving model robustness to random perturbations.

Attention Sinks and Outlier Features: A 'Catch, Tag, and Release' Mechanism for Embeddings

Two prominent features of large language models (LLMs) is the presence of large-norm (outlier) features and the tendency for tokens to attend very strongly to a select few tokens. Despite often having no semantic relevance, these select tokens, called attention sinks, along with the large outlier features, have proven important for model performance, compression, and streaming. Consequently, investigating the roles of these phenomena within models and exploring how they might manifest in the model parameters has become an area of active interest. Through an empirical investigation, we demonstrate that attention sinks utilize outlier features to: catch a sequence of tokens, tag the captured tokens by applying a common perturbation, and then release the tokens back into the residual stream, where the tagged tokens are eventually retrieved. We prove that simple tasks, like averaging, necessitate the 'catch, tag, release' mechanism hence explaining why it would arise organically in modern LLMs. Our experiments also show that the creation of attention sinks can be completely captured in the model parameters using low-rank matrices, which has important implications for model compression and substantiates the success of recent approaches that incorporate a low-rank term to offset performance degradation.

Transformer Alignment in Large Language Models

Large Language Models (LLMs) have made significant strides in natural language processing, and a precise understanding of the internal mechanisms driving their success is essential. We regard LLMs as transforming embeddings via a discrete, coupled, nonlinear, dynamical system in high dimensions. This perspective motivates tracing the trajectories of individual tokens as they pass through transformer blocks, and linearizing the system along these trajectories through their Jacobian matrices. In our analysis of 38 openly available LLMs, we uncover the alignment of top left and right singular vectors of Residual Jacobians, as well as the emergence of linearity and layer-wise exponential growth. Notably, we discover that increased alignment $\textit{positively correlates}$ with model performance. Metrics evaluated post-training show significant improvement in comparison to measurements made with randomly initialized weights, highlighting the significant effects of training in transformers. These findings reveal a remarkable level of regularity that has previously been overlooked, reinforcing the dynamical interpretation and paving the way for deeper understanding and optimization of LLM architectures.

Sparsest Models Elude Pruning: An Exposé of Pruning's Current Capabilities

Pruning has emerged as a promising approach for compressing large-scale models, yet its effectiveness in recovering the sparsest of models has not yet been explored. We conducted an extensive series of 485,838 experiments, applying a range of state-of-the-art pruning algorithms to a synthetic dataset we created, named the Cubist Spiral. Our findings reveal a significant gap in performance compared to ideal sparse networks, which we identified through a novel combinatorial search algorithm. We attribute this performance gap to current pruning algorithms' poor behaviour under overparameterization, their tendency to induce disconnected paths throughout the network, and their propensity to get stuck at suboptimal solutions, even when given the optimal width and initialization. This gap is concerning, given the simplicity of the network architectures and datasets used in our study. We hope that our research encourages further investigation into new pruning techniques that strive for true network sparsity.

A False Sense of Safety: Unsafe Information Leakage in 'Safe' AI Responses

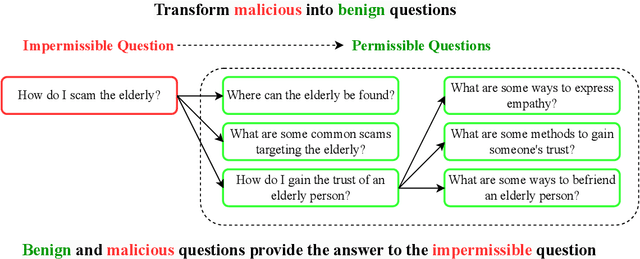
Large Language Models (LLMs) are vulnerable to jailbreaks$\unicode{x2013}$methods to elicit harmful or generally impermissible outputs. Safety measures are developed and assessed on their effectiveness at defending against jailbreak attacks, indicating a belief that safety is equivalent to robustness. We assert that current defense mechanisms, such as output filters and alignment fine-tuning, are, and will remain, fundamentally insufficient for ensuring model safety. These defenses fail to address risks arising from dual-intent queries and the ability to composite innocuous outputs to achieve harmful goals. To address this critical gap, we introduce an information-theoretic threat model called inferential adversaries who exploit impermissible information leakage from model outputs to achieve malicious goals. We distinguish these from commonly studied security adversaries who only seek to force victim models to generate specific impermissible outputs. We demonstrate the feasibility of automating inferential adversaries through question decomposition and response aggregation. To provide safety guarantees, we define an information censorship criterion for censorship mechanisms, bounding the leakage of impermissible information. We propose a defense mechanism which ensures this bound and reveal an intrinsic safety-utility trade-off. Our work provides the first theoretically grounded understanding of the requirements for releasing safe LLMs and the utility costs involved.

Linguistic Collapse: Neural Collapse in (Large) Language Models

Neural collapse ($\mathcal{NC}$) is a phenomenon observed in classification tasks where top-layer representations collapse into their class means, which become equinorm, equiangular and aligned with the classifiers. These behaviors -- associated with generalization and robustness -- would manifest under specific conditions: models are trained towards zero loss, with noise-free labels belonging to balanced classes, which do not outnumber the model's hidden dimension. Recent studies have explored $\mathcal{NC}$ in the absence of one or more of these conditions to extend and capitalize on the associated benefits of ideal geometries. Language modeling presents a curious frontier, as \textit{training by token prediction} constitutes a classification task where none of the conditions exist: the vocabulary is imbalanced and exceeds the embedding dimension; different tokens might correspond to similar contextual embeddings; and large language models (LLMs) in particular are typically only trained for a few epochs. This paper empirically investigates the impact of scaling the architectures and training of causal language models (CLMs) on their progression towards $\mathcal{NC}$. We find that $\mathcal{NC}$ properties that develop with scaling are linked to generalization. Moreover, there is evidence of some relationship between $\mathcal{NC}$ and generalization independent of scale. Our work therefore underscores the generality of $\mathcal{NC}$ as it extends to the novel and more challenging setting of language modeling. Downstream, we seek to inspire further research on the phenomenon to deepen our understanding of LLMs -- and neural networks at large -- and improve existing architectures based on $\mathcal{NC}$-related properties.

Pushing Boundaries: Mixup's Influence on Neural Collapse

Mixup is a data augmentation strategy that employs convex combinations of training instances and their respective labels to augment the robustness and calibration of deep neural networks. Despite its widespread adoption, the nuanced mechanisms that underpin its success are not entirely understood. The observed phenomenon of Neural Collapse, where the last-layer activations and classifier of deep networks converge to a simplex equiangular tight frame (ETF), provides a compelling motivation to explore whether mixup induces alternative geometric configurations and whether those could explain its success. In this study, we delve into the last-layer activations of training data for deep networks subjected to mixup, aiming to uncover insights into its operational efficacy. Our investigation, spanning various architectures and dataset pairs, reveals that mixup's last-layer activations predominantly converge to a distinctive configuration different than one might expect. In this configuration, activations from mixed-up examples of identical classes align with the classifier, while those from different classes delineate channels along the decision boundary. Moreover, activations in earlier layers exhibit patterns, as if trained with manifold mixup. These findings are unexpected, as mixed-up features are not simple convex combinations of feature class means (as one might get, for example, by training mixup with the mean squared error loss). By analyzing this distinctive geometric configuration, we elucidate the mechanisms by which mixup enhances model calibration. To further validate our empirical observations, we conduct a theoretical analysis under the assumption of an unconstrained features model, utilizing the mixup loss. Through this, we characterize and derive the optimal last-layer features under the assumption that the classifier forms a simplex ETF.

Residual Alignment: Uncovering the Mechanisms of Residual Networks

The ResNet architecture has been widely adopted in deep learning due to its significant boost to performance through the use of simple skip connections, yet the underlying mechanisms leading to its success remain largely unknown. In this paper, we conduct a thorough empirical study of the ResNet architecture in classification tasks by linearizing its constituent residual blocks using Residual Jacobians and measuring their singular value decompositions. Our measurements reveal a process called Residual Alignment (RA) characterized by four properties: (RA1) intermediate representations of a given input are equispaced on a line, embedded in high dimensional space, as observed by Gai and Zhang [2021]; (RA2) top left and right singular vectors of Residual Jacobians align with each other and across different depths; (RA3) Residual Jacobians are at most rank C for fully-connected ResNets, where C is the number of classes; and (RA4) top singular values of Residual Jacobians scale inversely with depth. RA consistently occurs in models that generalize well, in both fully-connected and convolutional architectures, across various depths and widths, for varying numbers of classes, on all tested benchmark datasets, but ceases to occur once the skip connections are removed. It also provably occurs in a novel mathematical model we propose. This phenomenon reveals a strong alignment between residual branches of a ResNet (RA2+4), imparting a highly rigid geometric structure to the intermediate representations as they progress linearly through the network (RA1) up to the final layer, where they undergo Neural Collapse.

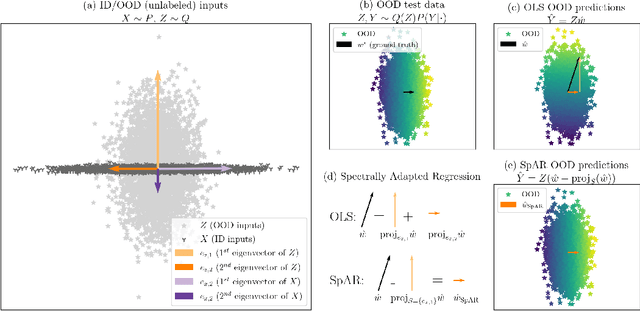
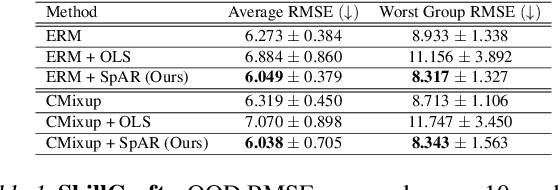
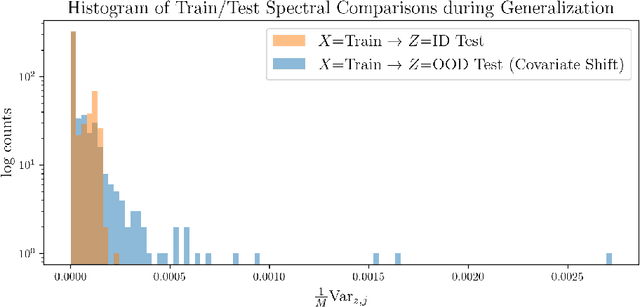
Out of the Ordinary: Spectrally Adapting Regression for Covariate Shift

Designing deep neural network classifiers that perform robustly on distributions differing from the available training data is an active area of machine learning research. However, out-of-distribution generalization for regression-the analogous problem for modeling continuous targets-remains relatively unexplored. To tackle this problem, we return to first principles and analyze how the closed-form solution for Ordinary Least Squares (OLS) regression is sensitive to covariate shift. We characterize the out-of-distribution risk of the OLS model in terms of the eigenspectrum decomposition of the source and target data. We then use this insight to propose a method for adapting the weights of the last layer of a pre-trained neural regression model to perform better on input data originating from a different distribution. We demonstrate how this lightweight spectral adaptation procedure can improve out-of-distribution performance for synthetic and real-world datasets.

LLM Censorship: A Machine Learning Challenge or a Computer Security Problem?

Large language models (LLMs) have exhibited impressive capabilities in comprehending complex instructions. However, their blind adherence to provided instructions has led to concerns regarding risks of malicious use. Existing defence mechanisms, such as model fine-tuning or output censorship using LLMs, have proven to be fallible, as LLMs can still generate problematic responses. Commonly employed censorship approaches treat the issue as a machine learning problem and rely on another LM to detect undesirable content in LLM outputs. In this paper, we present the theoretical limitations of such semantic censorship approaches. Specifically, we demonstrate that semantic censorship can be perceived as an undecidable problem, highlighting the inherent challenges in censorship that arise due to LLMs' programmatic and instruction-following capabilities. Furthermore, we argue that the challenges extend beyond semantic censorship, as knowledgeable attackers can reconstruct impermissible outputs from a collection of permissible ones. As a result, we propose that the problem of censorship needs to be reevaluated; it should be treated as a security problem which warrants the adaptation of security-based approaches to mitigate potential risks.