Survey Descent: A Multipoint Generalization of Gradient Descent for Nonsmooth Optimization
Paper and Code
Dec 29, 2021
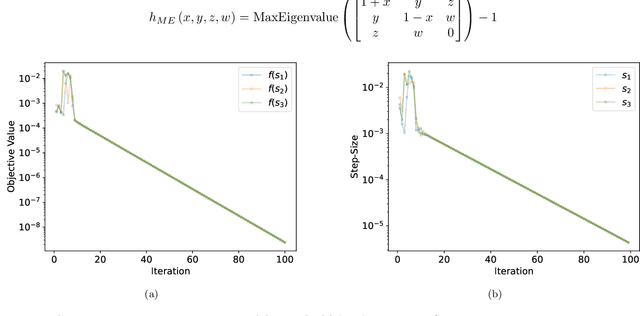
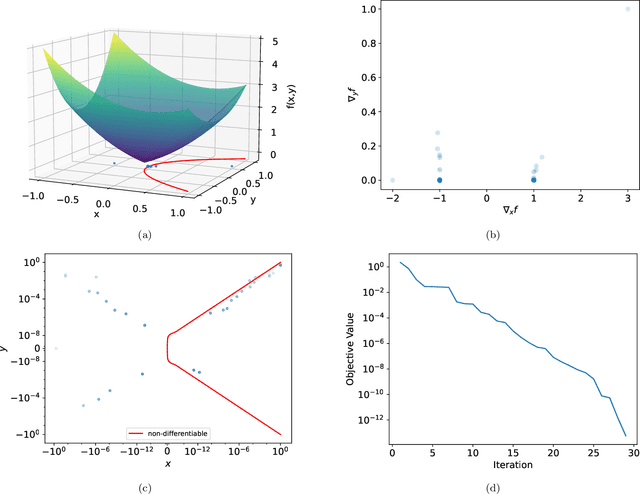
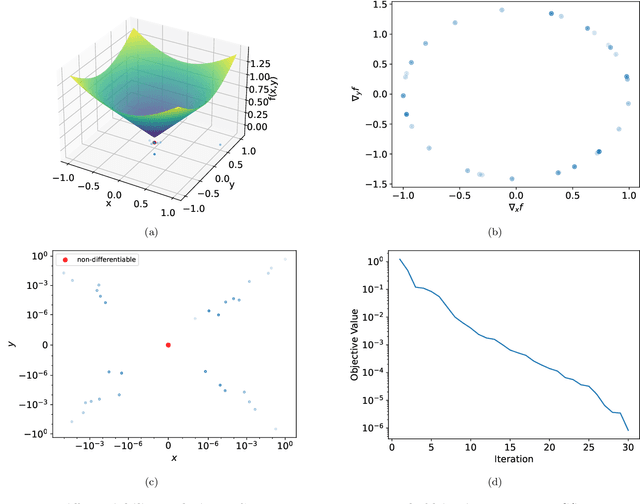
For strongly convex objectives that are smooth, the classical theory of gradient descent ensures linear convergence relative to the number of gradient evaluations. An analogous nonsmooth theory is challenging: even when the objective is smooth at every iterate, the corresponding local models are unstable, and traditional remedies need unpredictably many cutting planes. We instead propose a multipoint generalization of the gradient descent iteration for local optimization. While designed with general objectives in mind, we are motivated by a "max-of-smooth" model that captures subdifferential dimension at optimality. We prove linear convergence when the objective is itself max-of-smooth, and experiments suggest a more general phenomenon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge