Temporal Concept Dynamics in Diffusion Models via Prompt-Conditioned Interventions

Diffusion models are usually evaluated by their final outputs, gradually denoising random noise into meaningful images. Yet, generation unfolds along a trajectory, and analyzing this dynamic process is crucial for understanding how controllable, reliable, and predictable these models are in terms of their success/failure modes. In this work, we ask the question: when does noise turn into a specific concept (e.g., age) and lock in the denoising trajectory? We propose PCI (Prompt-Conditioned Intervention) to study this question. PCI is a training-free and model-agnostic framework for analyzing concept dynamics through diffusion time. The central idea is the analysis of Concept Insertion Success (CIS), defined as the probability that a concept inserted at a given timestep is preserved and reflected in the final image, offering a way to characterize the temporal dynamics of concept formation. Applied to several state-of-the-art text-to-image diffusion models and a broad taxonomy of concepts, PCI reveals diverse temporal behaviors across diffusion models, in which certain phases of the trajectory are more favorable to specific concepts even within the same concept type. These findings also provide actionable insights for text-driven image editing, highlighting when interventions are most effective without requiring access to model internals or training, and yielding quantitatively stronger edits that achieve a balance of semantic accuracy and content preservation than strong baselines. Code is available at: https://github.com/adagorgun/PCI-Prompt-Controlled-Interventions

Disentangling Polysemantic Channels in Convolutional Neural Networks

Mechanistic interpretability is concerned with analyzing individual components in a (convolutional) neural network (CNN) and how they form larger circuits representing decision mechanisms. These investigations are challenging since CNNs frequently learn polysemantic channels that encode distinct concepts, making them hard to interpret. To address this, we propose an algorithm to disentangle a specific kind of polysemantic channel into multiple channels, each responding to a single concept. Our approach restructures weights in a CNN, utilizing that different concepts within the same channel exhibit distinct activation patterns in the previous layer. By disentangling these polysemantic features, we enhance the interpretability of CNNs, ultimately improving explanatory techniques such as feature visualizations.

VITAL: More Understandable Feature Visualization through Distribution Alignment and Relevant Information Flow

Neural networks are widely adopted to solve complex and challenging tasks. Especially in high-stakes decision-making, understanding their reasoning process is crucial, yet proves challenging for modern deep networks. Feature visualization (FV) is a powerful tool to decode what information neurons are responding to and hence to better understand the reasoning behind such networks. In particular, in FV we generate human-understandable images that reflect the information detected by neurons of interest. However, current methods often yield unrecognizable visualizations, exhibiting repetitive patterns and visual artifacts that are hard to understand for a human. To address these problems, we propose to guide FV through statistics of real image features combined with measures of relevant network flow to generate prototypical images. Our approach yields human-understandable visualizations that both qualitatively and quantitatively improve over state-of-the-art FVs across various architectures. As such, it can be used to decode which information the network uses, complementing mechanistic circuits that identify where it is encoded. Code is available at: https://github.com/adagorgun/VITAL

Escaping Plato's Cave: Robust Conceptual Reasoning through Interpretable 3D Neural Object Volumes

With the rise of neural networks, especially in high-stakes applications, these networks need two properties (i) robustness and (ii) interpretability to ensure their safety. Recent advances in classifiers with 3D volumetric object representations have demonstrated a greatly enhanced robustness in out-of-distribution data. However, these 3D-aware classifiers have not been studied from the perspective of interpretability. We introduce CAVE - Concept Aware Volumes for Explanations - a new direction that unifies interpretability and robustness in image classification. We design an inherently-interpretable and robust classifier by extending existing 3D-aware classifiers with concepts extracted from their volumetric representations for classification. In an array of quantitative metrics for interpretability, we compare against different concept-based approaches across the explainable AI literature and show that CAVE discovers well-grounded concepts that are used consistently across images, while achieving superior robustness.

Unlocking Open-Set Language Accessibility in Vision Models

Visual classifiers offer high-dimensional feature representations that are challenging to interpret and analyze. Text, in contrast, provides a more expressive and human-friendly interpretable medium for understanding and analyzing model behavior. We propose a simple, yet powerful method for reformulating any visual classifier so that it can be accessed with open-set text queries without compromising its original performance. Our approach is label-free, efficient, and preserves the underlying classifier's distribution and reasoning processes. We thus unlock several text-based interpretability applications for any classifier. We apply our method on 40 visual classifiers and demonstrate two primary applications: 1) building both label-free and zero-shot concept bottleneck models and therefore converting any classifier to be inherently-interpretable and 2) zero-shot decoding of visual features into natural language. In both applications, we achieve state-of-the-art results, greatly outperforming existing works. Our method enables text approaches for interpreting visual classifiers.

Now you see me! A framework for obtaining class-relevant saliency maps

Neural networks are part of daily-life decision-making, including in high-stakes settings where understanding and transparency are key. Saliency maps have been developed to gain understanding into which input features neural networks use for a specific prediction. Although widely employed, these methods often result in overly general saliency maps that fail to identify the specific information that triggered the classification. In this work, we suggest a framework that allows to incorporate attributions across classes to arrive at saliency maps that actually capture the class-relevant information. On established benchmarks for attribution methods, including the grid-pointing game and randomization-based sanity checks, we show that our framework heavily boosts the performance of standard saliency map approaches. It is, by design, agnostic to model architectures and attribution methods and now allows to identify the distinguishing and shared features used for a model prediction.

Sailing in high-dimensional spaces: Low-dimensional embeddings through angle preservation

Low-dimensional embeddings (LDEs) of high-dimensional data are ubiquitous in science and engineering. They allow us to quickly understand the main properties of the data, identify outliers and processing errors, and inform the next steps of data analysis. As such, LDEs have to be faithful to the original high-dimensional data, i.e., they should represent the relationships that are encoded in the data, both at a local as well as global scale. The current generation of LDE approaches focus on reconstructing local distances between any pair of samples correctly, often out-performing traditional approaches aiming at all distances. For these approaches, global relationships are, however, usually strongly distorted, often argued to be an inherent trade-off between local and global structure learning for embeddings. We suggest a new perspective on LDE learning, reconstructing angles between data points. We show that this approach, Mercat, yields good reconstruction across a diverse set of experiments and metrics, and preserve structures well across all scales. Compared to existing work, our approach also has a simple formulation, facilitating future theoretical analysis and algorithmic improvements.

Not all tickets are equal and we know it: Guiding pruning with domain-specific knowledge

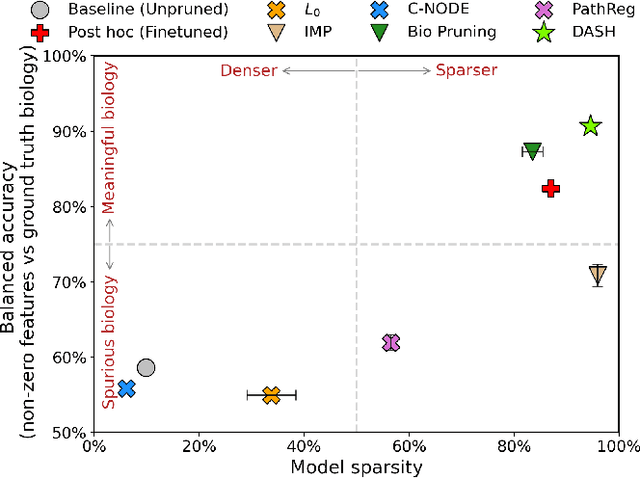
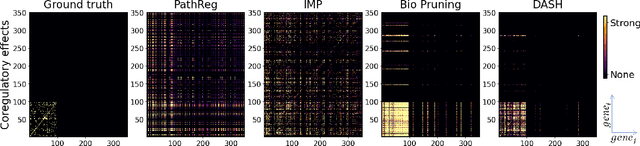
Neural structure learning is of paramount importance for scientific discovery and interpretability. Yet, contemporary pruning algorithms that focus on computational resource efficiency face algorithmic barriers to select a meaningful model that aligns with domain expertise. To mitigate this challenge, we propose DASH, which guides pruning by available domain-specific structural information. In the context of learning dynamic gene regulatory network models, we show that DASH combined with existing general knowledge on interaction partners provides data-specific insights aligned with biology. For this task, we show on synthetic data with ground truth information and two real world applications the effectiveness of DASH, which outperforms competing methods by a large margin and provides more meaningful biological insights. Our work shows that domain specific structural information bears the potential to improve model-derived scientific insights.

Finding Interpretable Class-Specific Patterns through Efficient Neural Search

Discovering patterns in data that best describe the differences between classes allows to hypothesize and reason about class-specific mechanisms. In molecular biology, for example, this bears promise of advancing the understanding of cellular processes differing between tissues or diseases, which could lead to novel treatments. To be useful in practice, methods that tackle the problem of finding such differential patterns have to be readily interpretable by domain experts, and scalable to the extremely high-dimensional data. In this work, we propose a novel, inherently interpretable binary neural network architecture DIFFNAPS that extracts differential patterns from data. DiffNaps is scalable to hundreds of thousands of features and robust to noise, thus overcoming the limitations of current state-of-the-art methods in large-scale applications such as in biology. We show on synthetic and real world data, including three biological applications, that, unlike its competitors, DiffNaps consistently yields accurate, succinct, and interpretable class descriptions

Understanding and Mitigating Classification Errors Through Interpretable Token Patterns

State-of-the-art NLP methods achieve human-like performance on many tasks, but make errors nevertheless. Characterizing these errors in easily interpretable terms gives insight into whether a classifier is prone to making systematic errors, but also gives a way to act and improve the classifier. We propose to discover those patterns of tokens that distinguish correct and erroneous predictions as to obtain global and interpretable descriptions for arbitrary NLP classifiers. We formulate the problem of finding a succinct and non-redundant set of such patterns in terms of the Minimum Description Length principle. Through an extensive set of experiments, we show that our method, Premise, performs well in practice. Unlike existing solutions, it recovers ground truth, even on highly imbalanced data over large vocabularies. In VQA and NER case studies, we confirm that it gives clear and actionable insight into the systematic errors made by NLP classifiers.