Kernel spectral joint embeddings for high-dimensional noisy datasets using duo-landmark integral operators

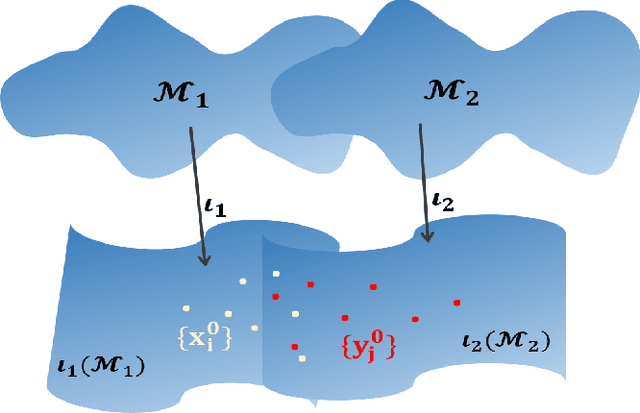
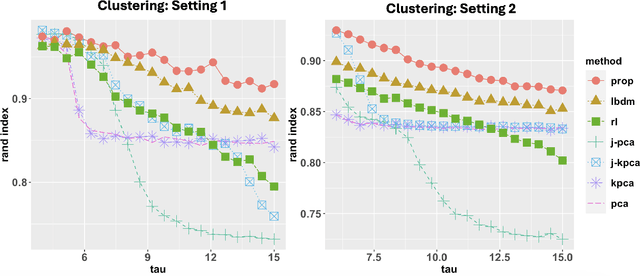
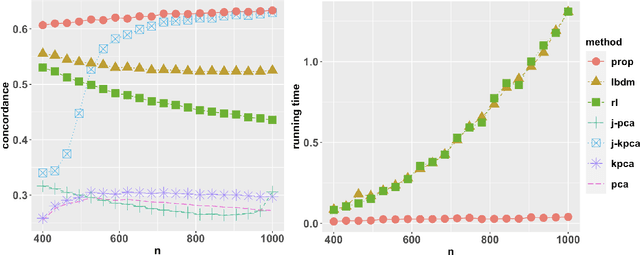
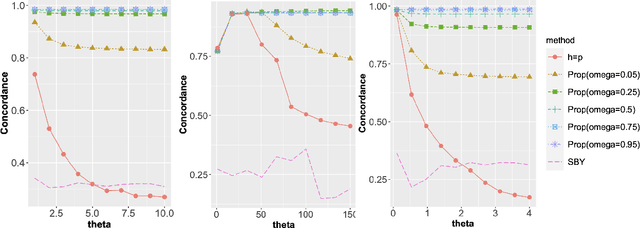
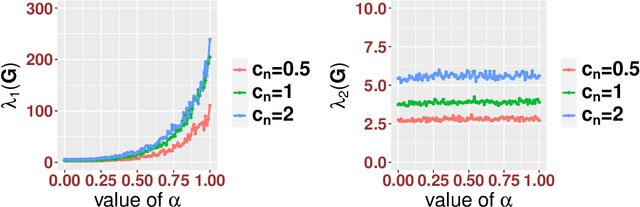
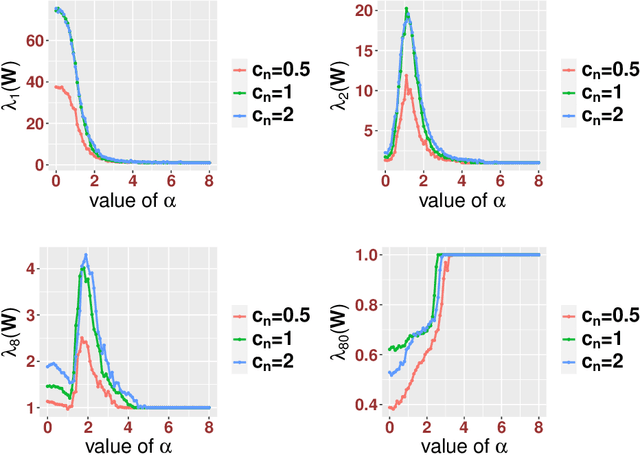
Integrative analysis of multiple heterogeneous datasets has become standard practice in many research fields, especially in single-cell genomics and medical informatics. Existing approaches oftentimes suffer from limited power in capturing nonlinear structures, insufficient account of noisiness and effects of high-dimensionality, lack of adaptivity to signals and sample sizes imbalance, and their results are sometimes difficult to interpret. To address these limitations, we propose a novel kernel spectral method that achieves joint embeddings of two independently observed high-dimensional noisy datasets. The proposed method automatically captures and leverages possibly shared low-dimensional structures across datasets to enhance embedding quality. The obtained low-dimensional embeddings can be utilized for many downstream tasks such as simultaneous clustering, data visualization, and denoising. The proposed method is justified by rigorous theoretical analysis. Specifically, we show the consistency of our method in recovering the low-dimensional noiseless signals, and characterize the effects of the signal-to-noise ratios on the rates of convergence. Under a joint manifolds model framework, we establish the convergence of ultimate embeddings to the eigenfunctions of some newly introduced integral operators. These operators, referred to as duo-landmark integral operators, are defined by the convolutional kernel maps of some reproducing kernel Hilbert spaces (RKHSs). These RKHSs capture the either partially or entirely shared underlying low-dimensional nonlinear signal structures of the two datasets. Our numerical experiments and analyses of two single-cell omics datasets demonstrate the empirical advantages of the proposed method over existing methods in both embeddings and several downstream tasks.

Learning Low-Dimensional Nonlinear Structures from High-Dimensional Noisy Data: An Integral Operator Approach

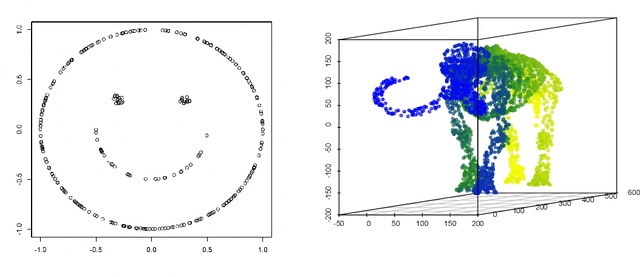
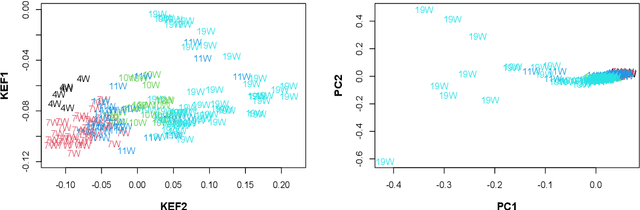
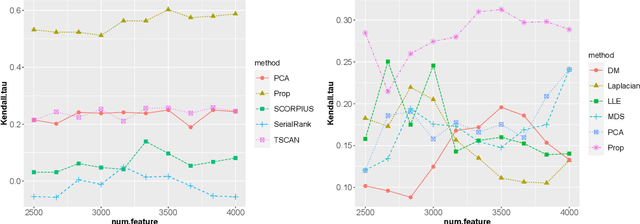
We propose a kernel-spectral embedding algorithm for learning low-dimensional nonlinear structures from high-dimensional and noisy observations, where the datasets are assumed to be sampled from an intrinsically low-dimensional manifold and corrupted by high-dimensional noise. The algorithm employs an adaptive bandwidth selection procedure which does not rely on prior knowledge of the underlying manifold. The obtained low-dimensional embeddings can be further utilized for downstream purposes such as data visualization, clustering and prediction. Our method is theoretically justified and practically interpretable. Specifically, we establish the convergence of the final embeddings to their noiseless counterparts when the dimension and size of the samples are comparably large, and characterize the effect of the signal-to-noise ratio on the rate of convergence and phase transition. We also prove convergence of the embeddings to the eigenfunctions of an integral operator defined by the kernel map of some reproducing kernel Hilbert space capturing the underlying nonlinear structures. Numerical simulations and analysis of three real datasets show the superior empirical performance of the proposed method, compared to many existing methods, on learning various manifolds in diverse applications.

How do kernel-based sensor fusion algorithms behave under high dimensional noise?

We study the behavior of two kernel based sensor fusion algorithms, nonparametric canonical correlation analysis (NCCA) and alternating diffusion (AD), under the nonnull setting that the clean datasets collected from two sensors are modeled by a common low dimensional manifold embedded in a high dimensional Euclidean space and the datasets are corrupted by high dimensional noise. We establish the asymptotic limits and convergence rates for the eigenvalues of the associated kernel matrices assuming that the sample dimension and sample size are comparably large, where NCCA and AD are conducted using the Gaussian kernel. It turns out that both the asymptotic limits and convergence rates depend on the signal-to-noise ratio (SNR) of each sensor and selected bandwidths. On one hand, we show that if NCCA and AD are directly applied to the noisy point clouds without any sanity check, it may generate artificial information that misleads scientists' interpretation. On the other hand, we prove that if the bandwidths are selected adequately, both NCCA and AD can be made robust to high dimensional noise when the SNRs are relatively large.

Phase transition of graph Laplacian of high dimensional noisy random point cloud

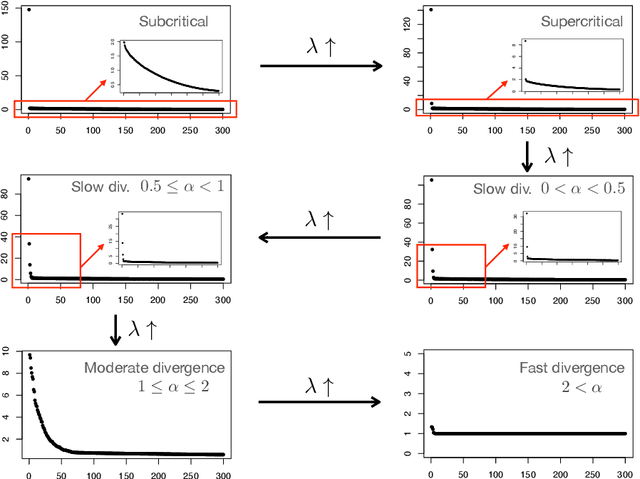
We systematically explore the spectral distribution of kernel-based graph Laplacian constructed from high dimensional and noisy random point cloud in the nonnull setup. An interesting phase transition phenomenon is reported, which is characterized by the signal-to-noise ratio (SNR). We quantify how the signal and noise interact over different SNR regimes; for example, how signal information pops out the Marchenko-Pastur bulk. Motivated by the analysis, an adaptive bandwidth selection algorithm is provided and proved, which coincides with the common practice in real data. Simulated data is provided to support the theoretical findings. Our results paves the way towards a foundation for statistical inference of various kernel-based unsupervised learning algorithms, like eigenmap, diffusion map and their variations, for real data analysis.

Modified Multidimensional Scaling and High Dimensional Clustering

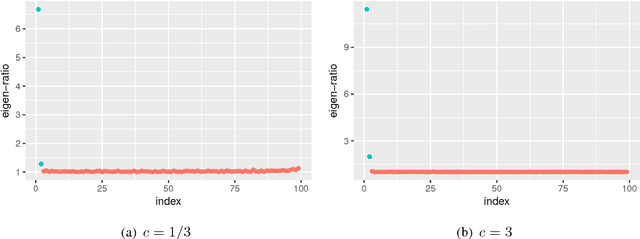
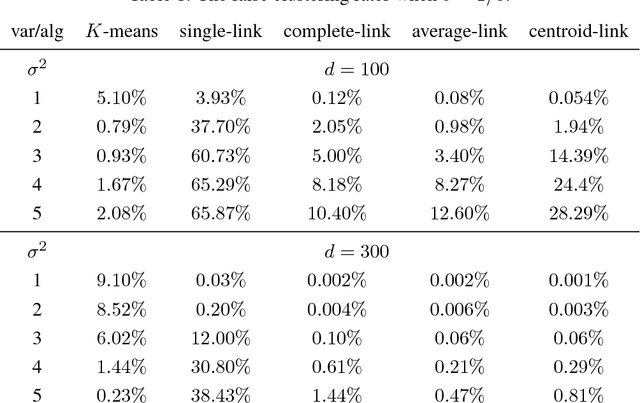
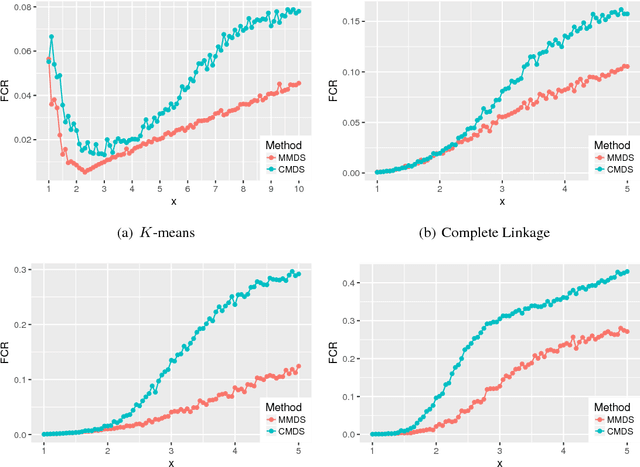
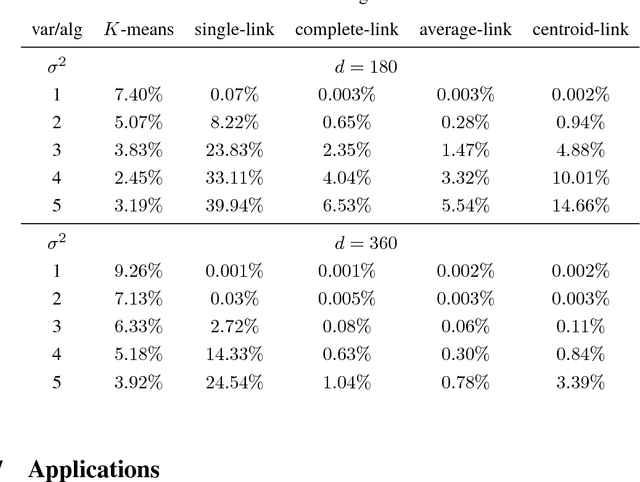
Multidimensional scaling is an important dimension reduction tool in statistics and machine learning. Yet few theoretical results characterizing its statistical performance exist, not to mention any in high dimensions. By considering a unified framework that includes low, moderate and high dimensions, we study multidimensional scaling in the setting of clustering noisy data. Our results suggest that, in order to achieve consistent estimation of the embedding scheme, the classical multidimensional scaling needs to be modified, especially when the noise level increases. To this end, we propose {\it modified multidimensional scaling} which applies a nonlinear transformation to the sample eigenvalues. The nonlinear transformation depends on the dimensionality, sample size and unknown moment. We show that modified multidimensional scaling followed by various clustering algorithms can achieve exact recovery, i.e., all the cluster labels can be recovered correctly with probability tending to one. Numerical simulations and two real data applications lend strong support to our proposed methodology. As a byproduct, we unify and improve existing results on the $\ell_{\infty}$ bound for eigenvectors under only low bounded moment conditions. This can be of independent interest.