Accelerate Speculative Decoding with Sparse Computation in Verification

Speculative decoding accelerates autoregressive language model inference by verifying multiple draft tokens in parallel. However, the verification stage often becomes the dominant computational bottleneck, especially for long-context inputs and mixture-of-experts (MoE) models. Existing sparsification methods are designed primarily for standard token-by-token autoregressive decoding to remove substantial computational redundancy in LLMs. This work systematically adopts different sparse methods on the verification stage of the speculative decoding and identifies structured redundancy across multiple dimensions. Based on these observations, we propose a sparse verification framework that jointly sparsifies attention, FFN, and MoE components during the verification stage to reduce the dominant computation cost. The framework further incorporates an inter-draft token and inter-layer retrieval reuse strategy to further reduce redundant computation without introducing additional training. Extensive experiments across summarization, question answering, and mathematical reasoning datasets demonstrate that the proposed methods achieve favorable efficiency-accuracy trade-offs, while maintaining stable acceptance length.

OpenSubject: Leveraging Video-Derived Identity and Diversity Priors for Subject-driven Image Generation and Manipulation

Despite the promising progress in subject-driven image generation, current models often deviate from the reference identities and struggle in complex scenes with multiple subjects. To address this challenge, we introduce OpenSubject, a video-derived large-scale corpus with 2.5M samples and 4.35M images for subject-driven generation and manipulation. The dataset is built with a four-stage pipeline that exploits cross-frame identity priors. (i) Video Curation. We apply resolution and aesthetic filtering to obtain high-quality clips. (ii) Cross-Frame Subject Mining and Pairing. We utilize vision-language model (VLM)-based category consensus, local grounding, and diversity-aware pairing to select image pairs. (iii) Identity-Preserving Reference Image Synthesis. We introduce segmentation map-guided outpainting to synthesize the input images for subject-driven generation and box-guided inpainting to generate input images for subject-driven manipulation, together with geometry-aware augmentations and irregular boundary erosion. (iv) Verification and Captioning. We utilize a VLM to validate synthesized samples, re-synthesize failed samples based on stage (iii), and then construct short and long captions. In addition, we introduce a benchmark covering subject-driven generation and manipulation, and then evaluate identity fidelity, prompt adherence, manipulation consistency, and background consistency with a VLM judge. Extensive experiments show that training with OpenSubject improves generation and manipulation performance, particularly in complex scenes.

LongCat-Image Technical Report

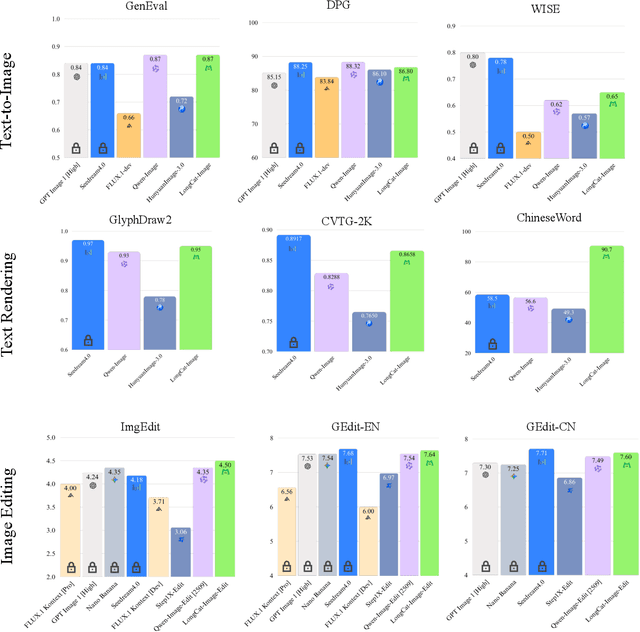
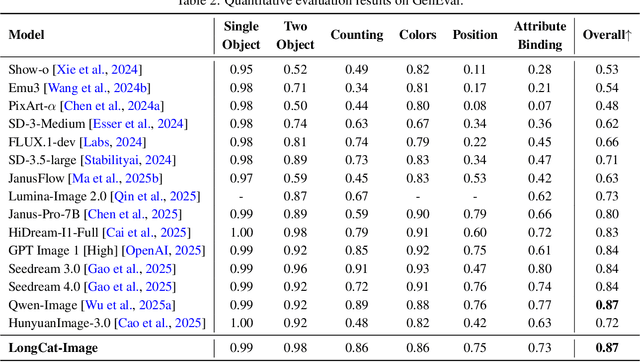
We introduce LongCat-Image, a pioneering open-source and bilingual (Chinese-English) foundation model for image generation, designed to address core challenges in multilingual text rendering, photorealism, deployment efficiency, and developer accessibility prevalent in current leading models. 1) We achieve this through rigorous data curation strategies across the pre-training, mid-training, and SFT stages, complemented by the coordinated use of curated reward models during the RL phase. This strategy establishes the model as a new state-of-the-art (SOTA), delivering superior text-rendering capabilities and remarkable photorealism, and significantly enhancing aesthetic quality. 2) Notably, it sets a new industry standard for Chinese character rendering. By supporting even complex and rare characters, it outperforms both major open-source and commercial solutions in coverage, while also achieving superior accuracy. 3) The model achieves remarkable efficiency through its compact design. With a core diffusion model of only 6B parameters, it is significantly smaller than the nearly 20B or larger Mixture-of-Experts (MoE) architectures common in the field. This ensures minimal VRAM usage and rapid inference, significantly reducing deployment costs. Beyond generation, LongCat-Image also excels in image editing, achieving SOTA results on standard benchmarks with superior editing consistency compared to other open-source works. 4) To fully empower the community, we have established the most comprehensive open-source ecosystem to date. We are releasing not only multiple model versions for text-to-image and image editing, including checkpoints after mid-training and post-training stages, but also the entire toolchain of training procedure. We believe that the openness of LongCat-Image will provide robust support for developers and researchers, pushing the frontiers of visual content creation.

Counteracting Matthew Effect in Self-Improvement of LVLMs through Head-Tail Re-balancing

Self-improvement has emerged as a mainstream paradigm for advancing the reasoning capabilities of large vision-language models (LVLMs), where models explore and learn from successful trajectories iteratively. However, we identify a critical issue during this process: the model excels at generating high-quality trajectories for simple queries (i.e., head data) but struggles with more complex ones (i.e., tail data). This leads to an imbalanced optimization that drives the model to prioritize simple reasoning skills, while hindering its ability to tackle more complex reasoning tasks. Over iterations, this imbalance becomes increasingly pronounced--a dynamic we term the "Matthew effect"--which ultimately hinders further model improvement and leads to performance bottlenecks. To counteract this challenge, we introduce four efficient strategies from two perspectives: distribution-reshaping and trajectory-resampling, to achieve head-tail re-balancing during the exploration-and-learning self-improvement process. Extensive experiments on Qwen2-VL-7B-Instruct and InternVL2.5-4B models across visual reasoning tasks demonstrate that our methods consistently improve visual reasoning capabilities, outperforming vanilla self-improvement by 3.86 points on average.

CATArena: Evaluation of LLM Agents through Iterative Tournament Competitions

Large Language Model (LLM) agents have evolved from basic text generation to autonomously completing complex tasks through interaction with external tools. However, current benchmarks mainly assess end-to-end performance in fixed scenarios, restricting evaluation to specific skills and suffering from score saturation and growing dependence on expert annotation as agent capabilities improve. In this work, we emphasize the importance of learning ability, including both self-improvement and peer-learning, as a core driver for agent evolution toward human-level intelligence. We propose an iterative, competitive peer-learning framework, which allows agents to refine and optimize their strategies through repeated interactions and feedback, thereby systematically evaluating their learning capabilities. To address the score saturation issue in current benchmarks, we introduce CATArena, a tournament-style evaluation platform featuring four diverse board and card games with open-ended scoring. By providing tasks without explicit upper score limits, CATArena enables continuous and dynamic evaluation of rapidly advancing agent capabilities. Experimental results and analyses involving both minimal and commercial code agents demonstrate that CATArena provides reliable, stable, and scalable benchmarking for core agent abilities, particularly learning ability and strategy coding.

AMO-Bench: Large Language Models Still Struggle in High School Math Competitions

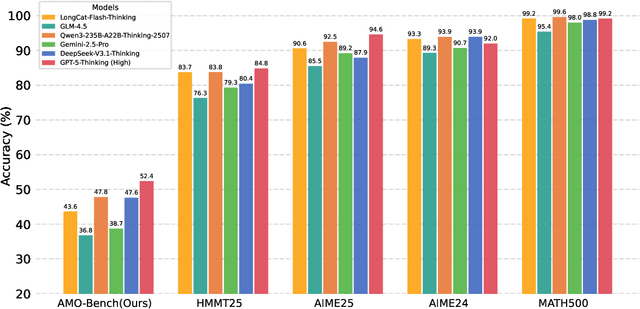
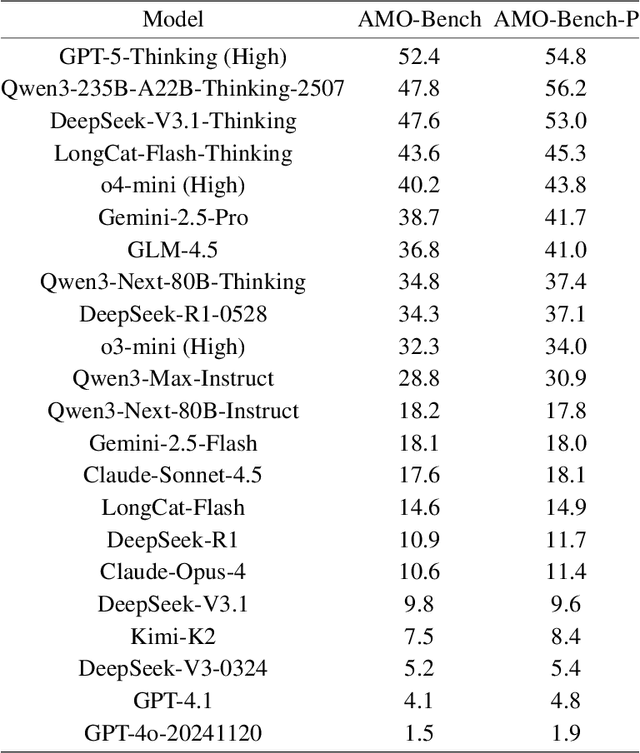
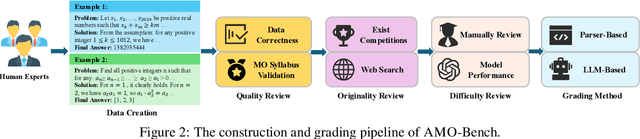
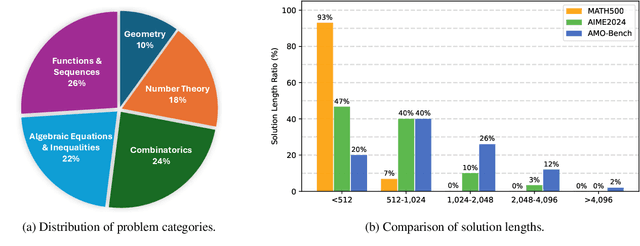
We present AMO-Bench, an Advanced Mathematical reasoning benchmark with Olympiad level or even higher difficulty, comprising 50 human-crafted problems. Existing benchmarks have widely leveraged high school math competitions for evaluating mathematical reasoning capabilities of large language models (LLMs). However, many existing math competitions are becoming less effective for assessing top-tier LLMs due to performance saturation (e.g., AIME24/25). To address this, AMO-Bench introduces more rigorous challenges by ensuring all 50 problems are (1) cross-validated by experts to meet at least the International Mathematical Olympiad (IMO) difficulty standards, and (2) entirely original problems to prevent potential performance leakages from data memorization. Moreover, each problem in AMO-Bench requires only a final answer rather than a proof, enabling automatic and robust grading for evaluation. Experimental results across 26 LLMs on AMO-Bench show that even the best-performing model achieves only 52.4% accuracy on AMO-Bench, with most LLMs scoring below 40%. Beyond these poor performances, our further analysis reveals a promising scaling trend with increasing test-time compute on AMO-Bench. These results highlight the significant room for improving the mathematical reasoning in current LLMs. We release AMO-Bench to facilitate further research into advancing the reasoning abilities of language models. https://amo-bench.github.io/

A Survey on LLM Mid-training

Recent advances in foundation models have highlighted the significant benefits of multi-stage training, with a particular emphasis on the emergence of mid-training as a vital stage that bridges pre-training and post-training. Mid-training is distinguished by its use of intermediate data and computational resources, systematically enhancing specified capabilities such as mathematics, coding, reasoning, and long-context extension, while maintaining foundational competencies. This survey provides a formal definition of mid-training for large language models (LLMs) and investigates optimization frameworks that encompass data curation, training strategies, and model architecture optimization. We analyze mainstream model implementations in the context of objective-driven interventions, illustrating how mid-training serves as a distinct and critical stage in the progressive development of LLM capabilities. By clarifying the unique contributions of mid-training, this survey offers a comprehensive taxonomy and actionable insights, supporting future research and innovation in the advancement of LLMs.

Autoformalizer with Tool Feedback

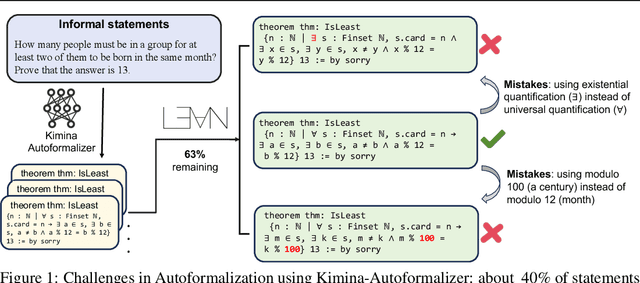
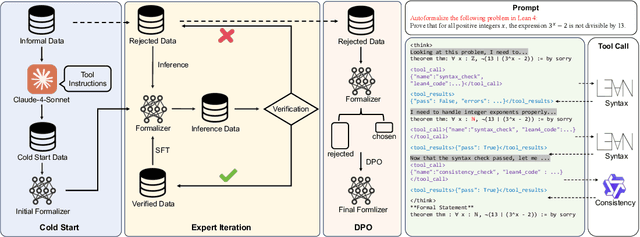
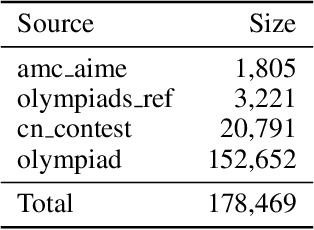
Autoformalization addresses the scarcity of data for Automated Theorem Proving (ATP) by translating mathematical problems from natural language into formal statements. Efforts in recent work shift from directly prompting large language models to training an end-to-end formalizer model from scratch, achieving remarkable advancements. However, existing formalizer still struggles to consistently generate valid statements that meet syntactic validity and semantic consistency. To address this issue, we propose the Autoformalizer with Tool Feedback (ATF), a novel approach that incorporates syntactic and consistency information as tools into the formalization process. By integrating Lean 4 compilers for syntax corrections and employing a multi-LLMs-as-judge approach for consistency validation, the model is able to adaptively refine generated statements according to the tool feedback, enhancing both syntactic validity and semantic consistency. The training of ATF involves a cold-start phase on synthetic tool-calling data, an expert iteration phase to improve formalization capabilities, and Direct Preference Optimization to alleviate ineffective revisions. Experimental results show that ATF markedly outperforms a range of baseline formalizer models, with its superior performance further validated by human evaluations. Subsequent analysis reveals that ATF demonstrates excellent inference scaling properties. Moreover, we open-source Numina-ATF, a dataset containing 750K synthetic formal statements to facilitate advancements in autoformalization and ATP research.

Making Mathematical Reasoning Adaptive

Mathematical reasoning is a primary indicator of large language models (LLMs) intelligence. However, existing LLMs exhibit failures of robustness and generalization. This paper attributes these deficiencies to spurious reasoning, i.e., producing answers from superficial features. To address this challenge, we propose the AdaR framework to enable adaptive reasoning, wherein models rely on problem-solving logic to produce answers. AdaR synthesizes logically equivalent queries by varying variable values, and trains models with RLVR on these data to penalize spurious logic while encouraging adaptive logic. To improve data quality, we extract the problem-solving logic from the original query and generate the corresponding answer by code execution, then apply a sanity check. Experimental results demonstrate that AdaR improves robustness and generalization, achieving substantial improvement in mathematical reasoning while maintaining high data efficiency. Analysis indicates that data synthesis and RLVR function in a coordinated manner to enable adaptive reasoning in LLMs. Subsequent analyses derive key design insights into the effect of critical factors and the applicability to instruct LLMs. Our project is available at https://github.com/LaiZhejian/AdaR

VitaBench: Benchmarking LLM Agents with Versatile Interactive Tasks in Real-world Applications

As LLM-based agents are increasingly deployed in real-life scenarios, existing benchmarks fail to capture their inherent complexity of handling extensive information, leveraging diverse resources, and managing dynamic user interactions. To address this gap, we introduce VitaBench, a challenging benchmark that evaluates agents on versatile interactive tasks grounded in real-world settings. Drawing from daily applications in food delivery, in-store consumption, and online travel services, VitaBench presents agents with the most complex life-serving simulation environment to date, comprising 66 tools. Through a framework that eliminates domain-specific policies, we enable flexible composition of these scenarios and tools, yielding 100 cross-scenario tasks (main results) and 300 single-scenario tasks. Each task is derived from multiple real user requests and requires agents to reason across temporal and spatial dimensions, utilize complex tool sets, proactively clarify ambiguous instructions, and track shifting user intent throughout multi-turn conversations. Moreover, we propose a rubric-based sliding window evaluator, enabling robust assessment of diverse solution pathways in complex environments and stochastic interactions. Our comprehensive evaluation reveals that even the most advanced models achieve only 30% success rate on cross-scenario tasks, and less than 50% success rate on others. Overall, we believe VitaBench will serve as a valuable resource for advancing the development of AI agents in practical real-world applications. The code, dataset, and leaderboard are available at https://vitabench.github.io/