Entropic Optimal Transport Eigenmaps for Nonlinear Alignment and Joint Embedding of High-Dimensional Datasets

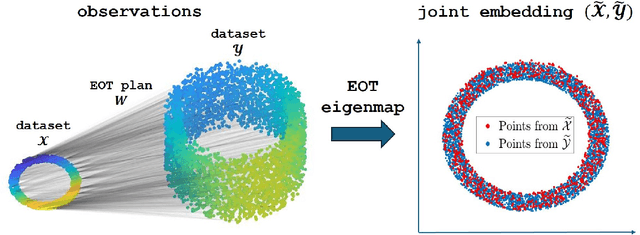
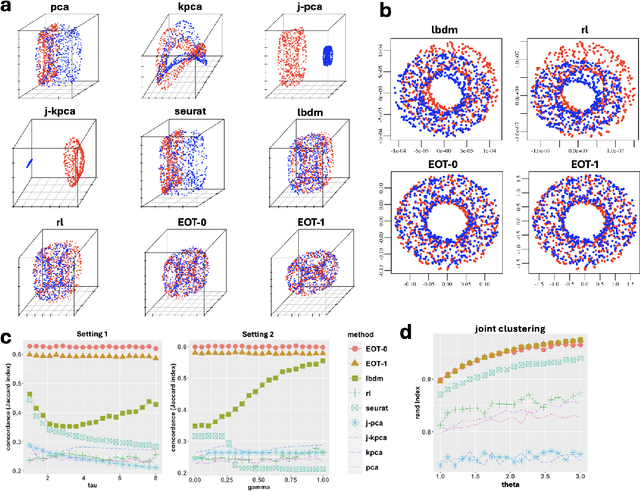
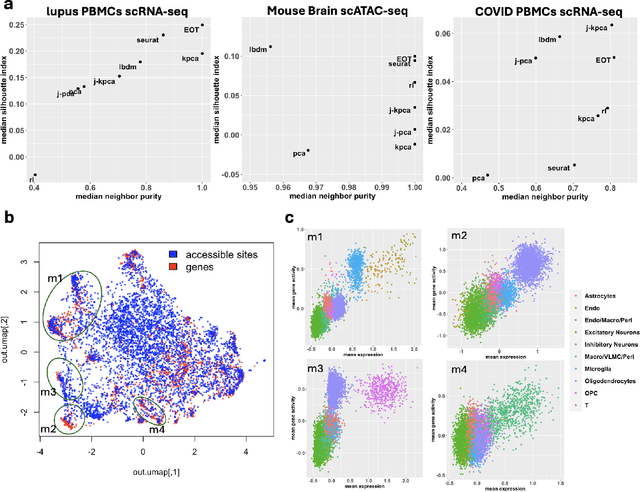
Embedding high-dimensional data into a low-dimensional space is an indispensable component of data analysis. In numerous applications, it is necessary to align and jointly embed multiple datasets from different studies or experimental conditions. Such datasets may share underlying structures of interest but exhibit individual distortions, resulting in misaligned embeddings using traditional techniques. In this work, we propose \textit{Entropic Optimal Transport (EOT) eigenmaps}, a principled approach for aligning and jointly embedding a pair of datasets with theoretical guarantees. Our approach leverages the leading singular vectors of the EOT plan matrix between two datasets to extract their shared underlying structure and align the datasets accordingly in a common embedding space. We interpret our approach as an inter-data variant of the classical Laplacian eigenmaps and diffusion maps embeddings, showing that it enjoys many favorable analogous properties. We then analyze a data-generative model where two observed high-dimensional datasets share latent variables on a common low-dimensional manifold, but each dataset is subject to data-specific translation, scaling, nuisance structures, and noise. We show that in a high-dimensional asymptotic regime, the EOT plan recovers the shared manifold structure by approximating a kernel function evaluated at the locations of the latent variables. Subsequently, we provide a geometric interpretation of our embedding by relating it to the eigenfunctions of population-level operators encoding the density and geometry of the shared manifold. Finally, we showcase the performance of our approach for data integration and embedding through simulations and analyses of real-world biological data, demonstrating its advantages over alternative methods in challenging scenarios.

Robust Inference of Manifold Density and Geometry by Doubly Stochastic Scaling

The Gaussian kernel and its traditional normalizations (e.g., row-stochastic) are popular approaches for assessing similarities between data points, commonly used for manifold learning and clustering, as well as supervised and semi-supervised learning on graphs. In many practical situations, the data can be corrupted by noise that prohibits traditional affinity matrices from correctly assessing similarities, especially if the noise magnitudes vary considerably across the data, e.g., under heteroskedasticity or outliers. An alternative approach that provides a more stable behavior under noise is the doubly stochastic normalization of the Gaussian kernel. In this work, we investigate this normalization in a setting where points are sampled from an unknown density on a low-dimensional manifold embedded in high-dimensional space and corrupted by possibly strong, non-identically distributed, sub-Gaussian noise. We establish the pointwise concentration of the doubly stochastic affinity matrix and its scaling factors around certain population forms. We then utilize these results to develop several tools for robust inference. First, we derive a robust density estimator that can substantially outperform the standard kernel density estimator under high-dimensional noise. Second, we provide estimators for the pointwise noise magnitudes, the pointwise signal magnitudes, and the pairwise Euclidean distances between clean data points. Lastly, we derive robust graph Laplacian normalizations that approximate popular manifold Laplacians, including the Laplace Beltrami operator, showing that the local geometry of the manifold can be recovered under high-dimensional noise. We exemplify our results in simulations and on real single-cell RNA-sequencing data. In the latter, we show that our proposed normalizations are robust to technical variability associated with different cell types.

Bi-stochastically normalized graph Laplacian: convergence to manifold Laplacian and robustness to outlier noise

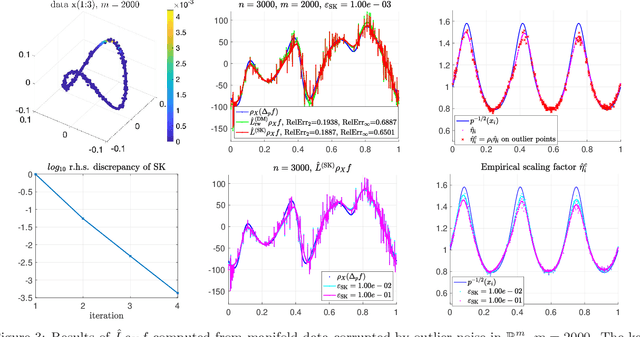
Bi-stochastic normalization of kernelized graph affinity matrix provides an alternative normalization scheme for graph Laplacian methods in graph-based data analysis and can be computed efficiently by Sinkhorn-Knopp (SK) iterations in practice. This paper proves the convergence of the bi-stochastically normalized graph Laplacian to manifold (weighted-)Laplacian with rates when $n$ data points are i.i.d. sampled from a general $d$-dimensional manifold embedded in a possibly high-dimensional space. Under certain joint limit of $n \to \infty$ and kernel bandwidth $\epsilon \to 0$, the point-wise convergence rate of the graph Laplacian operator (under 2-norm) is proved to be $ O( n^{-1/(d/2+3)})$ at finite large $n$ up to log factors, achieved at the scaling of $\epsilon \sim n^{-1/(d/2+3)} $. When the manifold data are corrupted by outlier noise, we theoretically prove the graph Laplacian point-wise consistency which matches the rate for clean manifold data up to an additional error term proportional to the boundedness of mutual inner-products of the noise vectors. Our analysis suggests that, under the setting being considered in this paper, not exact bi-stochastic normalization but an approximate one will achieve the same consistency rate. Motivated by the analysis, we propose an approximate and constrained matrix scaling problem that can be solved by SK iterations with early termination, and apply to simulated manifold data both clean and with outlier noise. Numerical experiments support our theoretical results and show the robustness of bi-stochastically normalized graph Laplacian to outlier noise.

Doubly-Stochastic Normalization of the Gaussian Kernel is Robust to Heteroskedastic Noise

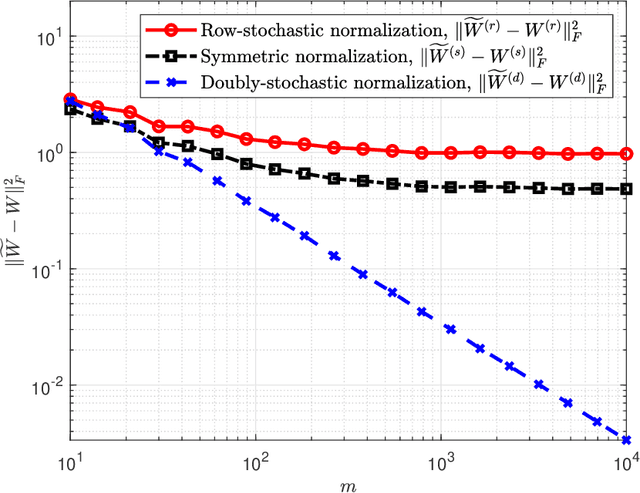
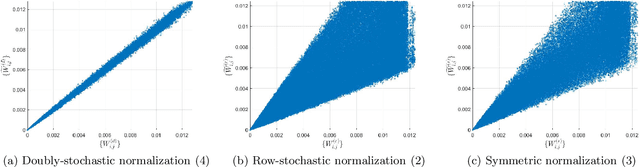
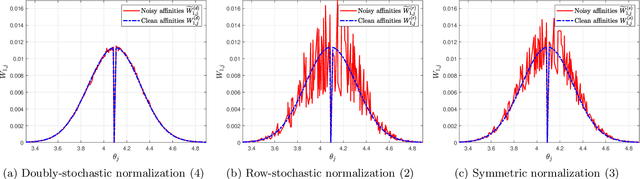
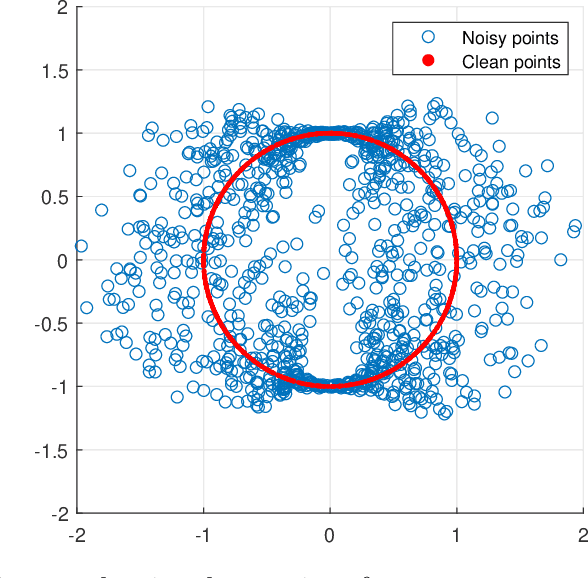
A fundamental step in many data-analysis techniques is the construction of an affinity matrix describing similarities between data points. When the data points reside in Euclidean space, a widespread approach is to from an affinity matrix by the Gaussian kernel with pairwise distances, and to follow with a certain normalization (e.g. the row-stochastic normalization or its symmetric variant). We demonstrate that the doubly-stochastic normalization of the Gaussian kernel with zero main diagonal (i.e. no self loops) is robust to heteroskedastic noise. That is, the doubly-stochastic normalization is advantageous in that it automatically accounts for observations with different noise variances. Specifically, we prove that in a suitable high-dimensional setting where heteroskedastic noise does not concentrate too much in any particular direction in space, the resulting (doubly-stochastic) noisy affinity matrix converges to its clean counterpart with rate $m^{-1/2}$, where $m$ is the ambient dimension. We demonstrate this result numerically, and show that in contrast, the popular row-stochastic and symmetric normalizations behave unfavorably under heteroskedastic noise. Furthermore, we provide a prototypical example of simulated single-cell RNA sequence data with strong intrinsic heteroskedasticity, where the advantage of the doubly-stochastic normalization for exploratory analysis is evident.

KLT Picker: Particle Picking Using Data-Driven Optimal Templates

Particle picking is currently a critical step in the cryo-EM single particle reconstruction pipeline. Despite extensive work on this problem, for many data sets it is still challenging, especially for low SNR micrographs. We present the KLT (Karhunen Loeve Transform) picker, which is fully automatic and requires as an input only the approximated particle size. In particular, it does not require any manual picking. Our method is designed especially to handle low SNR micrographs. It is based on learning a set of optimal templates through the use of multi-variate statistical analysis via the Karhunen Loeve Transform. We evaluate the KLT picker on publicly available data sets and present high-quality results with minimal manual effort.

Steerable Principal Components for Space-Frequency Localized Images

This paper describes a fast and accurate method for obtaining steerable principal components from a large dataset of images, assuming the images are well localized in space and frequency. The obtained steerable principal components are optimal for expanding the images in the dataset and all of their rotations. The method relies upon first expanding the images using a series of two-dimensional Prolate Spheroidal Wave Functions (PSWFs), where the expansion coefficients are evaluated using a specially designed numerical integration scheme. Then, the expansion coefficients are used to construct a rotationally-invariant covariance matrix which admits a block-diagonal structure, and the eigen-decomposition of its blocks provides us with the desired steerable principal components. The proposed method is shown to be faster then existing methods, while providing appropriate error bounds which guarantee its accuracy.

The steerable graph Laplacian and its application to filtering image data-sets

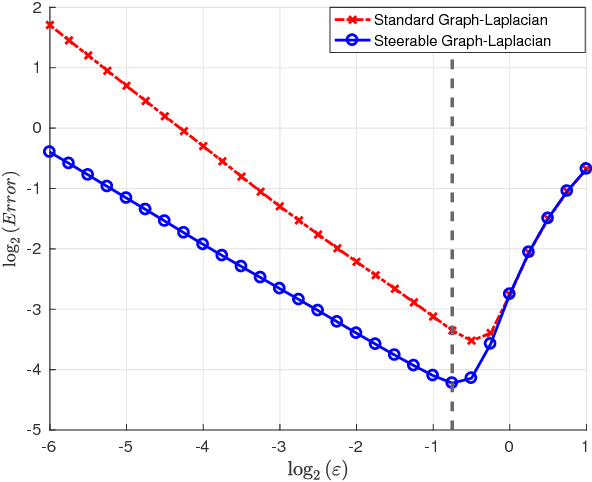
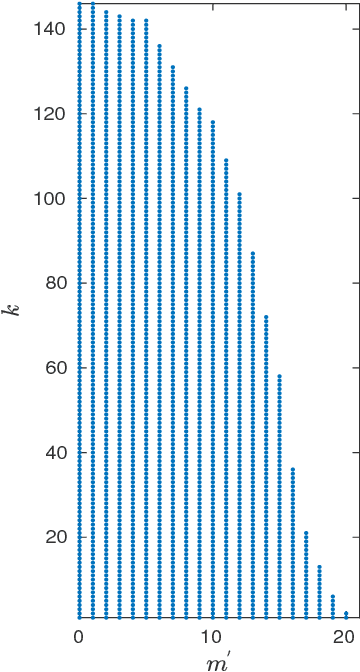
In recent years, improvements in various image acquisition techniques gave rise to the need for adaptive processing methods, aimed particularly for large datasets corrupted by noise and deformations. In this work, we consider datasets of images sampled from a low-dimensional manifold (i.e. an image-valued manifold), where the images can assume arbitrary planar rotations. To derive an adaptive and rotation-invariant framework for processing such datasets, we introduce a graph Laplacian (GL)-like operator over the dataset, termed ${\textit{steerable graph Laplacian}}$. Essentially, the steerable GL extends the standard GL by accounting for all (infinitely-many) planar rotations of all images. As it turns out, similarly to the standard GL, a properly normalized steerable GL converges to the Laplace-Beltrami operator on the low-dimensional manifold. However, the steerable GL admits an improved convergence rate compared to the GL, where the improved convergence behaves as if the intrinsic dimension of the underlying manifold is lower by one. Moreover, it is shown that the steerable GL admits eigenfunctions of the form of Fourier modes (along the orbits of the images' rotations) multiplied by eigenvectors of certain matrices, which can be computed efficiently by the FFT. For image datasets corrupted by noise, we employ a subset of these eigenfunctions to "filter" the dataset via a Fourier-like filtering scheme, essentially using all images and their rotations simultaneously. We demonstrate our filtering framework by de-noising simulated single-particle cryo-EM image datasets.