Doubly-Stochastic Normalization of the Gaussian Kernel is Robust to Heteroskedastic Noise

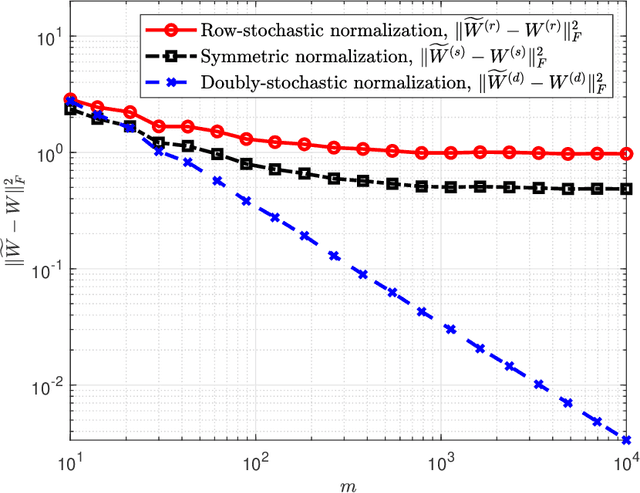
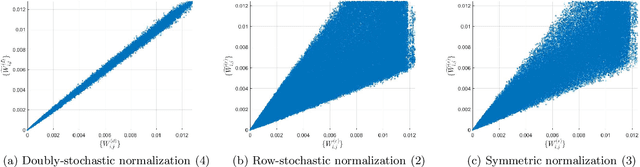
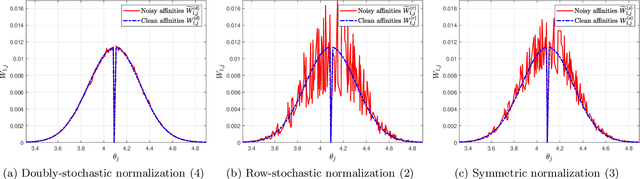
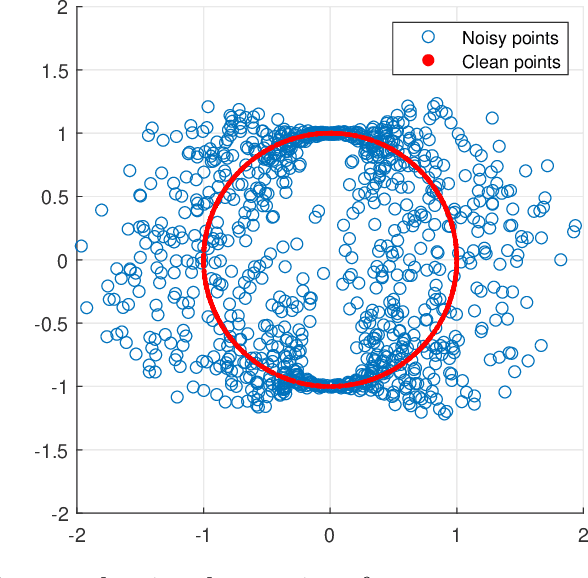
A fundamental step in many data-analysis techniques is the construction of an affinity matrix describing similarities between data points. When the data points reside in Euclidean space, a widespread approach is to from an affinity matrix by the Gaussian kernel with pairwise distances, and to follow with a certain normalization (e.g. the row-stochastic normalization or its symmetric variant). We demonstrate that the doubly-stochastic normalization of the Gaussian kernel with zero main diagonal (i.e. no self loops) is robust to heteroskedastic noise. That is, the doubly-stochastic normalization is advantageous in that it automatically accounts for observations with different noise variances. Specifically, we prove that in a suitable high-dimensional setting where heteroskedastic noise does not concentrate too much in any particular direction in space, the resulting (doubly-stochastic) noisy affinity matrix converges to its clean counterpart with rate $m^{-1/2}$, where $m$ is the ambient dimension. We demonstrate this result numerically, and show that in contrast, the popular row-stochastic and symmetric normalizations behave unfavorably under heteroskedastic noise. Furthermore, we provide a prototypical example of simulated single-cell RNA sequence data with strong intrinsic heteroskedasticity, where the advantage of the doubly-stochastic normalization for exploratory analysis is evident.