G-invariant diffusion maps

The diffusion maps embedding of data lying on a manifold have shown success in tasks ranging from dimensionality reduction and clustering, to data visualization. In this work, we consider embedding data sets which were sampled from a manifold which is closed under the action of a continuous matrix group. An example of such a data set are images who's planar rotations are arbitrary. The G-invariant graph Laplacian, introduced in a previous work of the authors, admits eigenfunctions in the form of tensor products between the elements of the irreducible unitary representations of the group and eigenvectors of certain matrices. We employ these eigenfunctions to derive diffusion maps that intrinsically account for the group action on the data. In particular, we construct both equivariant and invariant embeddings which can be used naturally to cluster and align the data points. We demonstrate the effectiveness of our construction with simulated data.

The G-invariant graph Laplacian

Graph Laplacian based algorithms for data lying on a manifold have been proven effective for tasks such as dimensionality reduction, clustering, and denoising. In this work, we consider data sets whose data point not only lie on a manifold, but are also closed under the action of a continuous group. An example of such data set is volumes that line on a low dimensional manifold, where each volume may be rotated in three-dimensional space. We introduce the G-invariant graph Laplacian that generalizes the graph Laplacian by accounting for the action of the group on the data set. We show that like the standard graph Laplacian, the G-invariant graph Laplacian converges to the Laplace-Beltrami operator on the data manifold, but with a significantly improved convergence rate. Furthermore, we show that the eigenfunctions of the G-invariant graph Laplacian admit the form of tensor products between the group elements and eigenvectors of certain matrices, which can be computed efficiently using FFT-type algorithms. We demonstrate our construction and its advantages on the problem of filtering data on a noisy manifold closed under the action of the special unitary group SU(2).

Signal enhancement for two-dimensional cryo-EM data processing

Different tasks in the computational pipeline of single-particle cryo-electron microscopy (cryo-EM) require enhancing the quality of the highly noisy raw images. To this end, we develop an efficient algorithm for signal enhancement of cryo-EM images. The enhanced images can be used for a variety of downstream tasks, such as 2-D classification, removing uninformative images, constructing {ab initio} models, generating templates for particle picking, providing a quick assessment of the data set, dimensionality reduction, and symmetry detection. The algorithm includes built-in quality measures to assess its performance and alleviate the risk of model bias. We demonstrate the effectiveness of the proposed algorithm on several experimental data sets. In particular, we show that the quality of the resulting images is high enough to produce ab initio models of $\sim 10$ \AA resolution. The algorithm is accompanied by a publicly available, documented and easy-to-use code.

Three-Dimensional Alignment of Density Maps in Cryo-Electron Microscopy

A common task in cryo-electron microscopy (cryo-EM) is to compare three-dimensional density maps of macromolecules. In this paper, we propose a fast, accurate and robust algorithm for aligning three-dimensional density maps, by exploiting common lines between projection images of the maps. The algorithm is fully automatic and handles rotations, reflections (handedness) and translations between the maps. In addition, the algorithm is applicable to any type of molecular symmetry without requiring any information regarding the symmetry of the maps. We evaluate our alignment algorithm on publicly available density maps, demonstrating its accuracy and efficiency. The algorithm is available at https://github.com/ShkolniskyLab/emalign.

A common lines approach for ab-initio modeling of molecules with tetrahedral and octahedral symmetry

A main task in cryo-electron microscopy single particle reconstruction is to find a three-dimensional model of a molecule given a set of its randomly oriented and positioned noisy projection-images. In this work, we propose an algorithm for ab-initio reconstruction for molecules with tetrahedral or octahedral symmetry. The algorithm exploits the multiple common lines between each pair of projection-images as well as self common lines within each image. It is robust to noise in the input images as it integrates the information from all images at once. The efficiency of the proposed algorithm is demonstrated using experimental cryo-electron microscopy data.

ASOCEM: Automatic Segmentation Of Contaminations in cryo-EM

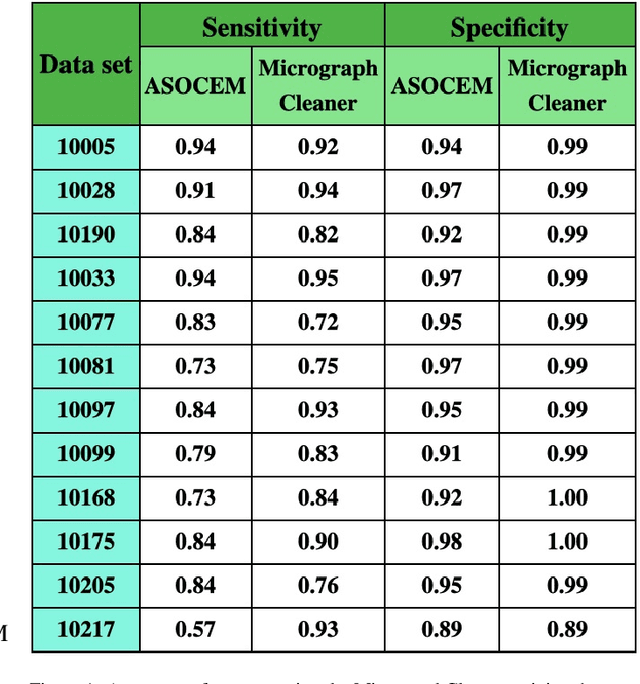
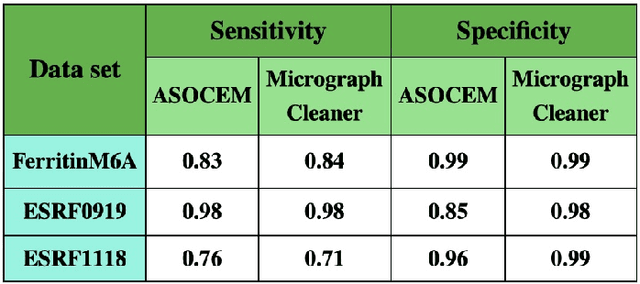
Particle picking is currently a critical step in the cryo-electron microscopy single particle reconstruction pipeline. Contaminations in the acquired micrographs severely degrade the performance of particle pickers, resulting is many ``non-particles'' in the collected stack of particles. In this paper, we present ASOCEM (Automatic Segmentation Of Contaminations in cryo-EM), an automatic method to detect and segment contaminations, which requires as an input only the approximated particle size. In particular, it does not require any parameter tuning nor manual intervention. Our method is based on the observation that the statistical distribution of contaminated regions is different from that of the rest of the micrograph. This nonrestrictive assumption allows to automatically detect various types of contaminations, from the carbon edges of the supporting grid to high contrast blobs of different sizes. We demonstrate the efficiency of our algorithm using various experimental data sets containing various types of contaminations. ASOCEM is integrated as part of the KLT picker \cite{ELDAR2020107473} and is available at \url{https://github.com/ShkolniskyLab/kltpicker2}.

A perturbation based out-of-sample extension framework

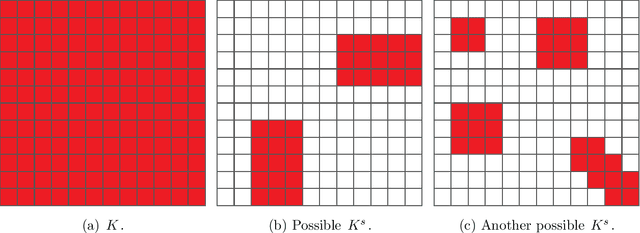
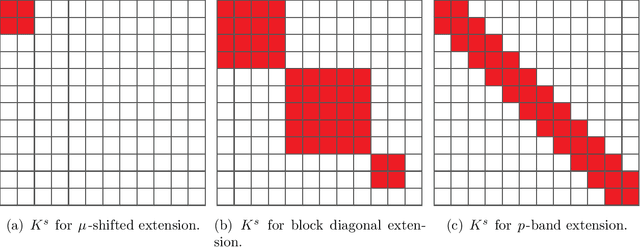
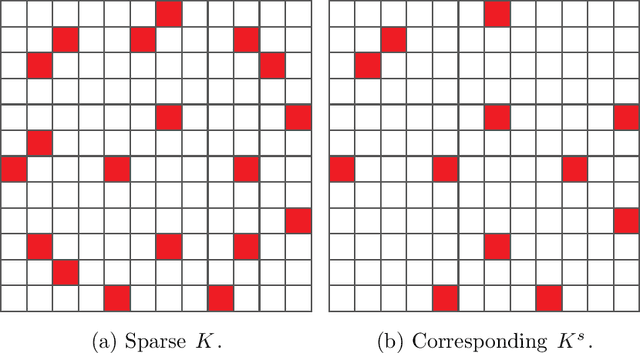
Out-of-sample extension is an important task in various kernel based non-linear dimensionality reduction algorithms. In this paper, we derive a perturbation based extension framework by extending results from classical perturbation theory. We prove that our extension framework generalizes the well-known Nystr{\"o}m method as well as some of its variants. We provide an error analysis for our extension framework, and suggest new forms of extension under this framework that take advantage of the structure of the kernel matrix. We support our theoretical results numerically and demonstrate the advantages of our extension framework both on synthetic and real data.

KLT Picker: Particle Picking Using Data-Driven Optimal Templates

Particle picking is currently a critical step in the cryo-EM single particle reconstruction pipeline. Despite extensive work on this problem, for many data sets it is still challenging, especially for low SNR micrographs. We present the KLT (Karhunen Loeve Transform) picker, which is fully automatic and requires as an input only the approximated particle size. In particular, it does not require any manual picking. Our method is designed especially to handle low SNR micrographs. It is based on learning a set of optimal templates through the use of multi-variate statistical analysis via the Karhunen Loeve Transform. We evaluate the KLT picker on publicly available data sets and present high-quality results with minimal manual effort.

ROIPCA: An Online PCA algorithm based on rank-one updates

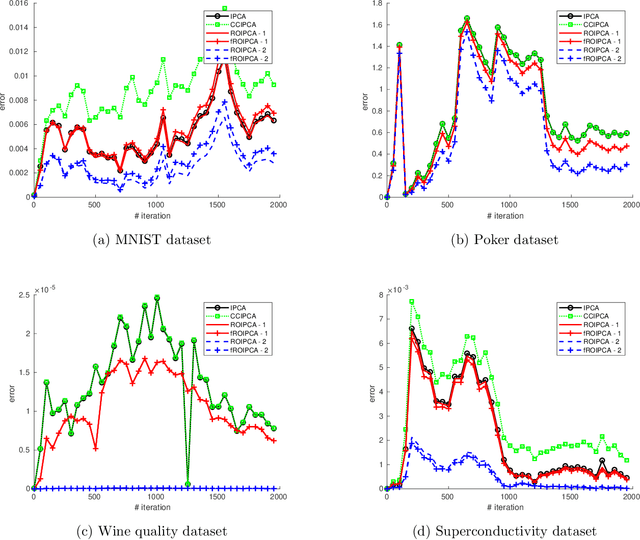
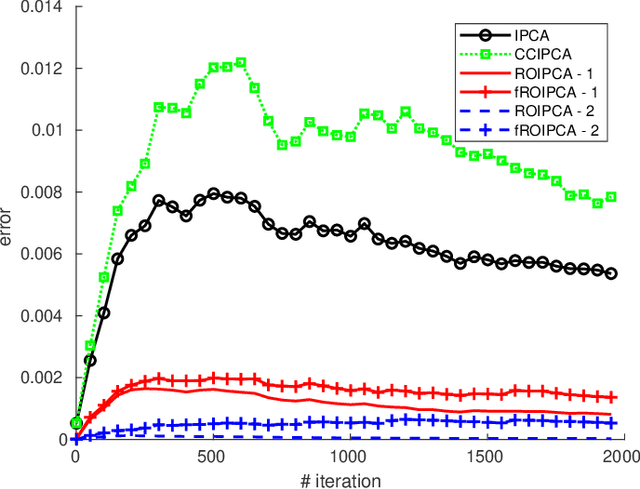
Principal components analysis (PCA) is a fundamental algorithm in data analysis. Its online version is useful in many modern applications where the data are too large to fit in memory, or when speed of calculation is important. In this paper we propose ROIPCA, an online PCA algorithm based on rank-one updates. ROIPCA is linear in both the dimension of the data and the number of components calculated. We demonstrate its advantages over existing state-of-the-art algorithms in terms of accuracy and running time.

Steerable Principal Components for Space-Frequency Localized Images

This paper describes a fast and accurate method for obtaining steerable principal components from a large dataset of images, assuming the images are well localized in space and frequency. The obtained steerable principal components are optimal for expanding the images in the dataset and all of their rotations. The method relies upon first expanding the images using a series of two-dimensional Prolate Spheroidal Wave Functions (PSWFs), where the expansion coefficients are evaluated using a specially designed numerical integration scheme. Then, the expansion coefficients are used to construct a rotationally-invariant covariance matrix which admits a block-diagonal structure, and the eigen-decomposition of its blocks provides us with the desired steerable principal components. The proposed method is shown to be faster then existing methods, while providing appropriate error bounds which guarantee its accuracy.