A perturbation based out-of-sample extension framework

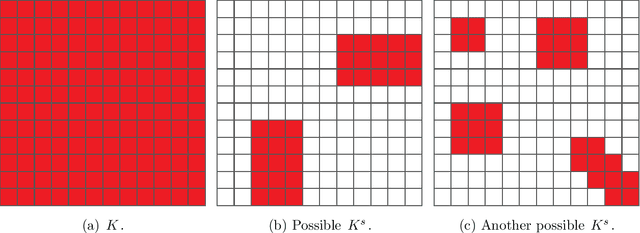
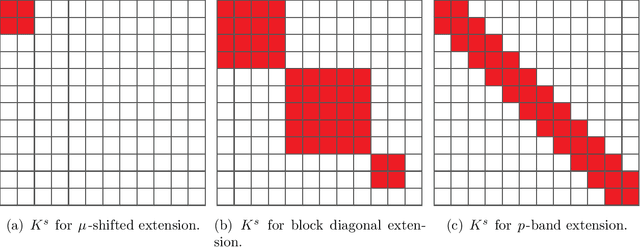
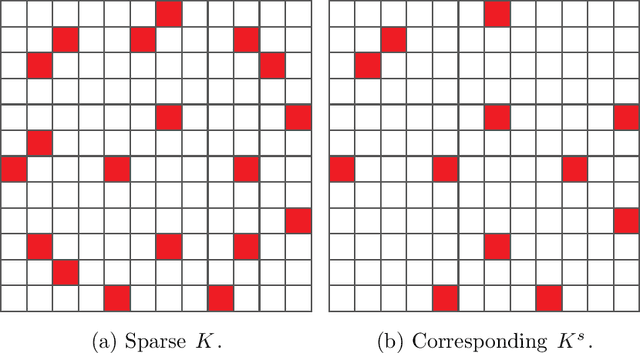
Out-of-sample extension is an important task in various kernel based non-linear dimensionality reduction algorithms. In this paper, we derive a perturbation based extension framework by extending results from classical perturbation theory. We prove that our extension framework generalizes the well-known Nystr{\"o}m method as well as some of its variants. We provide an error analysis for our extension framework, and suggest new forms of extension under this framework that take advantage of the structure of the kernel matrix. We support our theoretical results numerically and demonstrate the advantages of our extension framework both on synthetic and real data.

ROIPCA: An Online PCA algorithm based on rank-one updates

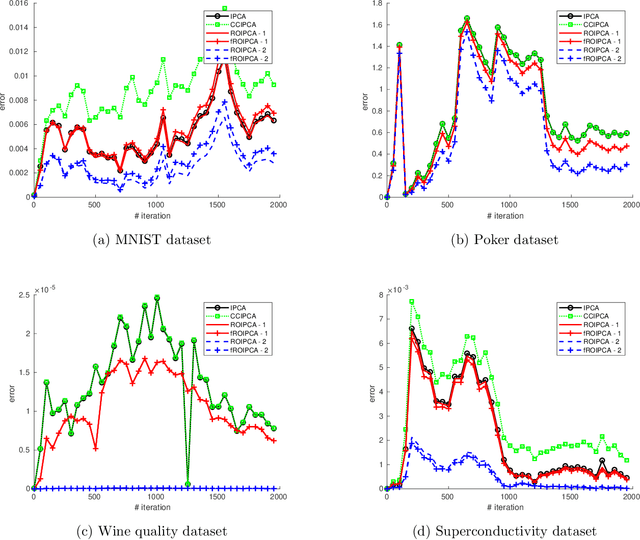
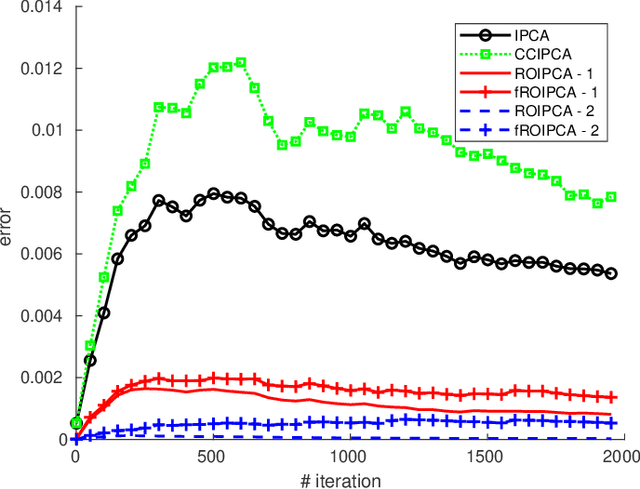
Principal components analysis (PCA) is a fundamental algorithm in data analysis. Its online version is useful in many modern applications where the data are too large to fit in memory, or when speed of calculation is important. In this paper we propose ROIPCA, an online PCA algorithm based on rank-one updates. ROIPCA is linear in both the dimension of the data and the number of components calculated. We demonstrate its advantages over existing state-of-the-art algorithms in terms of accuracy and running time.