Flow-based generative models as iterative algorithms in probability space

Generative AI (GenAI) has revolutionized data-driven modeling by enabling the synthesis of high-dimensional data across various applications, including image generation, language modeling, biomedical signal processing, and anomaly detection. Flow-based generative models provide a powerful framework for capturing complex probability distributions, offering exact likelihood estimation, efficient sampling, and deterministic transformations between distributions. These models leverage invertible mappings governed by Ordinary Differential Equations (ODEs), enabling precise density estimation and likelihood evaluation. This tutorial presents an intuitive mathematical framework for flow-based generative models, formulating them as neural network-based representations of continuous probability densities. We explore key theoretical principles, including the Wasserstein metric, gradient flows, and density evolution governed by ODEs, to establish convergence guarantees and bridge empirical advancements with theoretical insights. By providing a rigorous yet accessible treatment, we aim to equip researchers and practitioners with the necessary tools to effectively apply flow-based generative models in signal processing and machine learning.

Point processes with event time uncertainty

Point processes are widely used statistical models for uncovering the temporal patterns in dependent event data. In many applications, the event time cannot be observed exactly, calling for the incorporation of time uncertainty into the modeling of point process data. In this work, we introduce a framework to model time-uncertain point processes possibly on a network. We start by deriving the formulation in the continuous-time setting under a few assumptions motivated by application scenarios. After imposing a time grid, we obtain a discrete-time model that facilitates inference and can be computed by first-order optimization methods such as Gradient Descent or Variation inequality (VI) using batch-based Stochastic Gradient Descent (SGD). The parameter recovery guarantee is proved for VI inference at an $O(1/k)$ convergence rate using $k$ SGD steps. Our framework handles non-stationary processes by modeling the inference kernel as a matrix (or tensor on a network) and it covers the stationary process, such as the classical Hawkes process, as a special case. We experimentally show that the proposed approach outperforms previous General Linear model (GLM) baselines on simulated and real data and reveals meaningful causal relations on a Sepsis-associated Derangements dataset.

Improved convergence rate of kNN graph Laplacians

In graph-based data analysis, $k$-nearest neighbor ($k$NN) graphs are widely used due to their adaptivity to local data densities. Allowing weighted edges in the graph, the kernelized graph affinity provides a more general type of $k$NN graph where the $k$NN distance is used to set the kernel bandwidth adaptively. In this work, we consider a general class of $k$NN graph where the graph affinity is $W_{ij} = \epsilon^{-d/2} \; k_0 ( \| x_i - x_j \|^2 / \epsilon \phi( \widehat{\rho}(x_i), \widehat{\rho}(x_j) )^2 ) $, with $\widehat{\rho}(x)$ being the (rescaled) $k$NN distance at the point $x$, $\phi$ a symmetric bi-variate function, and $k_0$ a non-negative function on $[0,\infty)$. Under the manifold data setting, where $N$ i.i.d. samples $x_i$ are drawn from a density $p$ on a $d$-dimensional unknown manifold embedded in a high dimensional Euclidean space, we prove the point-wise convergence of the $k$NN graph Laplacian to the limiting manifold operator (depending on $p$) at the rate of $O(N^{-2/(d+6)}\,)$, up to a log factor, when $k_0$ and $\phi$ have $C^3$ regularity and satisfy other technical conditions. This fast rate is obtained when $\epsilon \sim N^{-2/(d+6)}\,$ and $k \sim N^{6/(d+6)}\,$, both at the optimal order to balance the theoretical bias and variance errors. When $k_0$ and $\phi$ have lower regularities, including when $k_0$ is a compactly supported function as in the standard $k$NN graph, the convergence rate degenerates to $O(N^{-1/(d+4)}\,)$. Our improved convergence rate is based on a refined analysis of the $k$NN estimator, which can be of independent interest. We validate our theory by numerical experiments on simulated data.

Local Flow Matching Generative Models

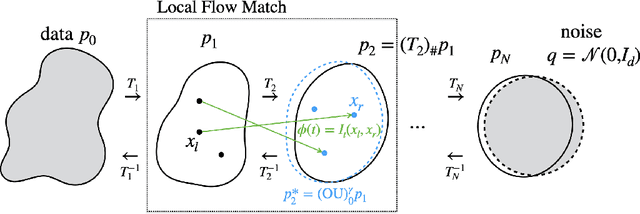
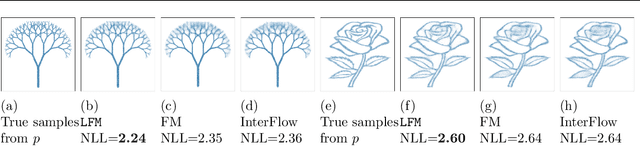
Flow Matching (FM) is a simulation-free method for learning a continuous and invertible flow to interpolate between two distributions, and in particular to generate data from noise in generative modeling. In this paper, we introduce Local Flow Matching (LFM), which learns a sequence of FM sub-models and each matches a diffusion process up to the time of the step size in the data-to-noise direction. In each step, the two distributions to be interpolated by the sub-model are closer to each other than data vs. noise, and this enables the use of smaller models with faster training. The stepwise structure of LFM is natural to be distilled and different distillation techniques can be adopted to speed up generation. Theoretically, we prove a generation guarantee of the proposed flow model in terms of the $\chi^2$-divergence between the generated and true data distributions. In experiments, we demonstrate the improved training efficiency and competitive generative performance of LFM compared to FM on the unconditional generation of tabular data and image datasets, and also on the conditional generation of robotic manipulation policies.

Posterior sampling via Langevin dynamics based on generative priors

Posterior sampling in high-dimensional spaces using generative models holds significant promise for various applications, including but not limited to inverse problems and guided generation tasks. Despite many recent developments, generating diverse posterior samples remains a challenge, as existing methods require restarting the entire generative process for each new sample, making the procedure computationally expensive. In this work, we propose efficient posterior sampling by simulating Langevin dynamics in the noise space of a pre-trained generative model. By exploiting the mapping between the noise and data spaces which can be provided by distilled flows or consistency models, our method enables seamless exploration of the posterior without the need to re-run the full sampling chain, drastically reducing computational overhead. Theoretically, we prove a guarantee for the proposed noise-space Langevin dynamics to approximate the posterior, assuming that the generative model sufficiently approximates the prior distribution. Our framework is experimentally validated on image restoration tasks involving noisy linear and nonlinear forward operators applied to LSUN-Bedroom (256 x 256) and ImageNet (64 x 64) datasets. The results demonstrate that our approach generates high-fidelity samples with enhanced semantic diversity even under a limited number of function evaluations, offering superior efficiency and performance compared to existing diffusion-based posterior sampling techniques.

Training Guarantees of Neural Network Classification Two-Sample Tests by Kernel Analysis

We construct and analyze a neural network two-sample test to determine whether two datasets came from the same distribution (null hypothesis) or not (alternative hypothesis). We perform time-analysis on a neural tangent kernel (NTK) two-sample test. In particular, we derive the theoretical minimum training time needed to ensure the NTK two-sample test detects a deviation-level between the datasets. Similarly, we derive the theoretical maximum training time before the NTK two-sample test detects a deviation-level. By approximating the neural network dynamics with the NTK dynamics, we extend this time-analysis to the realistic neural network two-sample test generated from time-varying training dynamics and finite training samples. A similar extension is done for the neural network two-sample test generated from time-varying training dynamics but trained on the population. To give statistical guarantees, we show that the statistical power associated with the neural network two-sample test goes to 1 as the neural network training samples and test evaluation samples go to infinity. Additionally, we prove that the training times needed to detect the same deviation-level in the null and alternative hypothesis scenarios are well-separated. Finally, we run some experiments showcasing a two-layer neural network two-sample test on a hard two-sample test problem and plot a heatmap of the statistical power of the two-sample test in relation to training time and network complexity.

Flow-based distributionally robust optimization

We present a computationally efficient framework, called FlowDRO, for solving flow-based distributionally robust optimization (DRO) problems with Wasserstein uncertainty sets while aiming to find continuous worst-case distribution (also called the Least Favorable Distribution, LFD). The requirement for LFD to be continuous is so that the algorithm can be scalable to problems with larger sample sizes and achieve better generalization capability for the induced robust algorithms. To tackle the computationally challenging infinitely dimensional optimization problem, we leverage flow-based models and continuous-time invertible transport maps between the data distribution and the target distribution. We also develop a Wasserstein proximal gradient flow type of algorithm. In theory, we establish the equivalence of the solution by optimal transport map to the original formulation, as well as the dual form of the problem through Wasserstein calculus and Brenier theorem. In practice, we parameterize the transport maps by a sequence of neural networks progressively trained in blocks by gradient descent. Our computational framework is general, can handle high-dimensional data with large sample sizes, and can be useful for various applications. We demonstrate its usage in adversarial learning, distributionally robust hypothesis testing, and a new mechanism for data-driven distribution perturbation differential privacy, where the proposed method gives strong empirical performance on real high-dimensional data.

Convergence of flow-based generative models via proximal gradient descent in Wasserstein space

Flow-based generative models enjoy certain advantages in computing the data generation and the likelihood, and have recently shown competitive empirical performance. Compared to the accumulating theoretical studies on related score-based diffusion models, analysis of flow-based models, which are deterministic in both forward (data-to-noise) and reverse (noise-to-data) directions, remain sparse. In this paper, we provide a theoretical guarantee of generating data distribution by a progressive flow model, the so-called JKO flow model, which implements the Jordan-Kinderleherer-Otto (JKO) scheme in a normalizing flow network. Leveraging the exponential convergence of the proximal gradient descent (GD) in Wasserstein space, we prove the Kullback-Leibler (KL) guarantee of data generation by a JKO flow model to be $O(\varepsilon^2)$ when using $N \lesssim \log (1/\varepsilon)$ many JKO steps ($N$ Residual Blocks in the flow) where $\varepsilon $ is the error in the per-step first-order condition. The assumption on data density is merely a finite second moment, and the theory extends to data distributions without density and when there are inversion errors in the reverse process where we obtain KL-$W_2$ mixed error guarantees. The non-asymptotic convergence rate of the JKO-type $W_2$-proximal GD is proved for a general class of convex objective functionals that includes the KL divergence as a special case, which can be of independent interest.

Deep graph kernel point processes

Point process models are widely used to analyze asynchronous events occurring within a graph that reflect how different types of events influence one another. Predicting future events' times and types is a crucial task, and the size and topology of the graph add to the challenge of the problem. Recent neural point process models unveil the possibility of capturing intricate inter-event-category dependencies. However, such methods utilize an unfiltered history of events, including all event categories in the intensity computation for each target event type. In this work, we propose a graph point process method where event interactions occur based on a latent graph topology. The corresponding undirected graph has nodes representing event categories and edges indicating potential contribution relationships. We then develop a novel deep graph kernel to characterize the triggering and inhibiting effects between events. The intrinsic influence structures are incorporated via the graph neural network (GNN) model used to represent the learnable kernel. The computational efficiency of the GNN approach allows our model to scale to large graphs. Comprehensive experiments on synthetic and real-world data show the superior performance of our approach against the state-of-the-art methods in predicting future events and uncovering the relational structure among data.

G-invariant diffusion maps

The diffusion maps embedding of data lying on a manifold have shown success in tasks ranging from dimensionality reduction and clustering, to data visualization. In this work, we consider embedding data sets which were sampled from a manifold which is closed under the action of a continuous matrix group. An example of such a data set are images who's planar rotations are arbitrary. The G-invariant graph Laplacian, introduced in a previous work of the authors, admits eigenfunctions in the form of tensor products between the elements of the irreducible unitary representations of the group and eigenvectors of certain matrices. We employ these eigenfunctions to derive diffusion maps that intrinsically account for the group action on the data. In particular, we construct both equivariant and invariant embeddings which can be used naturally to cluster and align the data points. We demonstrate the effectiveness of our construction with simulated data.