Modeling Discrete Coating Degradation Events via Hawkes Processes

Forecasting the degradation of coated materials has long been a topic of critical interest in engineering, as it has enormous implications for both system maintenance and sustainable material use. Material degradation is affected by many factors, including the history of corrosion and characteristics of the environment, which can be measured by high-frequency sensors. However, the high volume of data produced by such sensors can inhibit efficient modeling and prediction. To alleviate this issue, we propose novel metrics for representing material degradation, taking the form of discrete degradation events. These events maintain the statistical properties of continuous sensor readings, such as correlation with time to coating failure and coefficient of variation at failure, but are composed of orders of magnitude fewer measurements. To forecast future degradation of the coating system, a marked Hawkes process models the events. We use the forecast of degradation to predict a future time of failure, exhibiting superior performance to the approach based on direct modeling of galvanic corrosion using continuous sensor measurements. While such maintenance is typically done on a regular basis, degradation models can enable informed condition-based maintenance, reducing unnecessary excess maintenance and preventing unexpected failures.

Posterior sampling via Langevin dynamics based on generative priors

Posterior sampling in high-dimensional spaces using generative models holds significant promise for various applications, including but not limited to inverse problems and guided generation tasks. Despite many recent developments, generating diverse posterior samples remains a challenge, as existing methods require restarting the entire generative process for each new sample, making the procedure computationally expensive. In this work, we propose efficient posterior sampling by simulating Langevin dynamics in the noise space of a pre-trained generative model. By exploiting the mapping between the noise and data spaces which can be provided by distilled flows or consistency models, our method enables seamless exploration of the posterior without the need to re-run the full sampling chain, drastically reducing computational overhead. Theoretically, we prove a guarantee for the proposed noise-space Langevin dynamics to approximate the posterior, assuming that the generative model sufficiently approximates the prior distribution. Our framework is experimentally validated on image restoration tasks involving noisy linear and nonlinear forward operators applied to LSUN-Bedroom (256 x 256) and ImageNet (64 x 64) datasets. The results demonstrate that our approach generates high-fidelity samples with enhanced semantic diversity even under a limited number of function evaluations, offering superior efficiency and performance compared to existing diffusion-based posterior sampling techniques.

Deep graph kernel point processes

Point process models are widely used to analyze asynchronous events occurring within a graph that reflect how different types of events influence one another. Predicting future events' times and types is a crucial task, and the size and topology of the graph add to the challenge of the problem. Recent neural point process models unveil the possibility of capturing intricate inter-event-category dependencies. However, such methods utilize an unfiltered history of events, including all event categories in the intensity computation for each target event type. In this work, we propose a graph point process method where event interactions occur based on a latent graph topology. The corresponding undirected graph has nodes representing event categories and edges indicating potential contribution relationships. We then develop a novel deep graph kernel to characterize the triggering and inhibiting effects between events. The intrinsic influence structures are incorporated via the graph neural network (GNN) model used to represent the learnable kernel. The computational efficiency of the GNN approach allows our model to scale to large graphs. Comprehensive experiments on synthetic and real-world data show the superior performance of our approach against the state-of-the-art methods in predicting future events and uncovering the relational structure among data.

Neural Stein critics with staged $L^2$-regularization

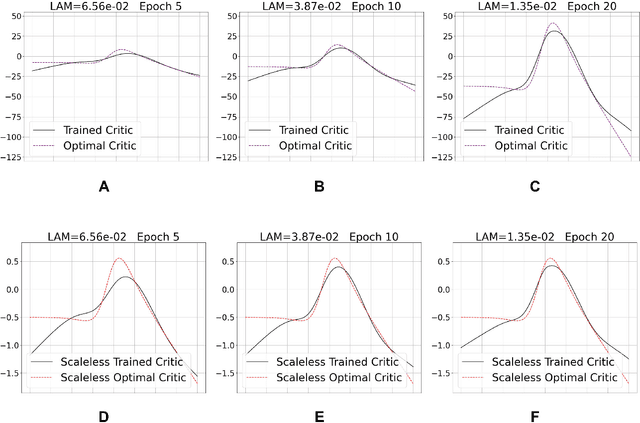
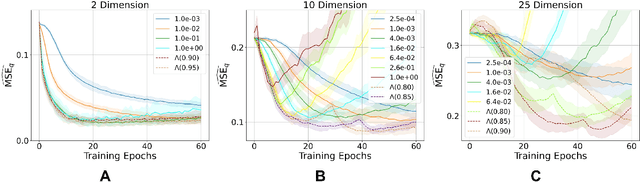
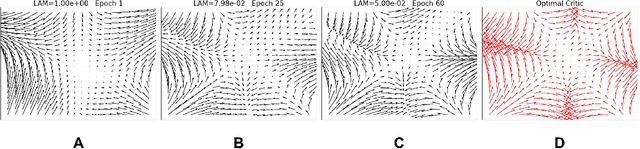
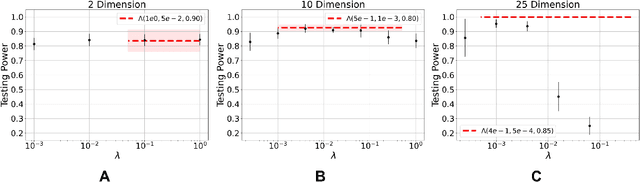
Learning to differentiate model distributions from observed data is a fundamental problem in statistics and machine learning, and high-dimensional data remains a challenging setting for such problems. Metrics that quantify the disparity in probability distributions, such as the Stein discrepancy, play an important role in statistical testing in high dimensions. In this paper, we consider the setting where one wishes to distinguish between data sampled from an unknown probability distribution and a nominal model distribution. While recent studies revealed that the optimal $L^2$-regularized Stein critic equals the difference of the score functions of two probability distributions up to a multiplicative constant, we investigate the role of $L^2$ regularization when training a neural network Stein discrepancy critic function. Motivated by the Neural Tangent Kernel theory of training neural networks, we develop a novel staging procedure for the weight of regularization over training time. This leverages the advantages of highly-regularized training at early times while also empirically delaying overfitting. Theoretically, we relate the training dynamic with large regularization weight to the kernel regression optimization of "lazy training" regime in early training times. The benefit of the staged $L^2$ regularization is demonstrated on simulated high dimensional distribution drift data and an application to evaluating generative models of image data.