Neural Stein critics with staged $L^2$-regularization
Paper and Code
Jul 07, 2022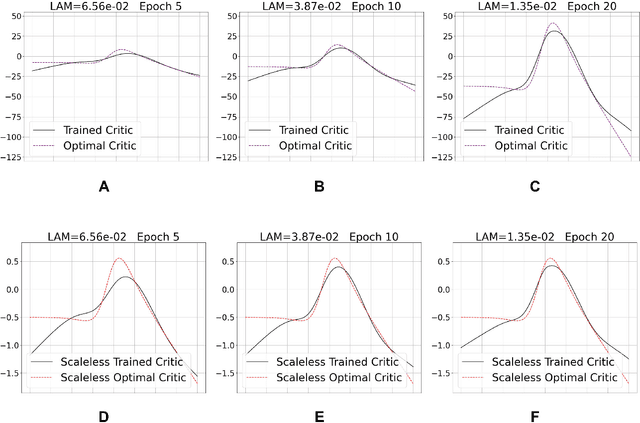
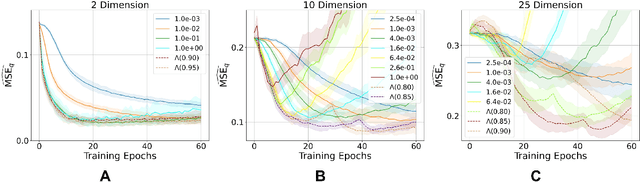
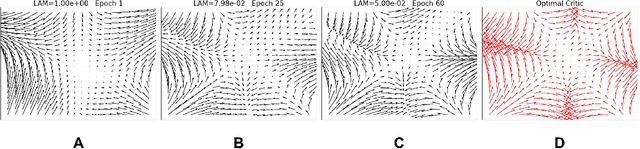
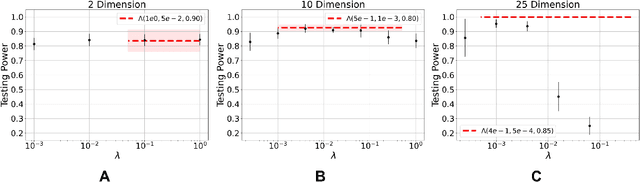
Learning to differentiate model distributions from observed data is a fundamental problem in statistics and machine learning, and high-dimensional data remains a challenging setting for such problems. Metrics that quantify the disparity in probability distributions, such as the Stein discrepancy, play an important role in statistical testing in high dimensions. In this paper, we consider the setting where one wishes to distinguish between data sampled from an unknown probability distribution and a nominal model distribution. While recent studies revealed that the optimal $L^2$-regularized Stein critic equals the difference of the score functions of two probability distributions up to a multiplicative constant, we investigate the role of $L^2$ regularization when training a neural network Stein discrepancy critic function. Motivated by the Neural Tangent Kernel theory of training neural networks, we develop a novel staging procedure for the weight of regularization over training time. This leverages the advantages of highly-regularized training at early times while also empirically delaying overfitting. Theoretically, we relate the training dynamic with large regularization weight to the kernel regression optimization of "lazy training" regime in early training times. The benefit of the staged $L^2$ regularization is demonstrated on simulated high dimensional distribution drift data and an application to evaluating generative models of image data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge