Probabilistic Robust Autoencoders for Anomaly Detection

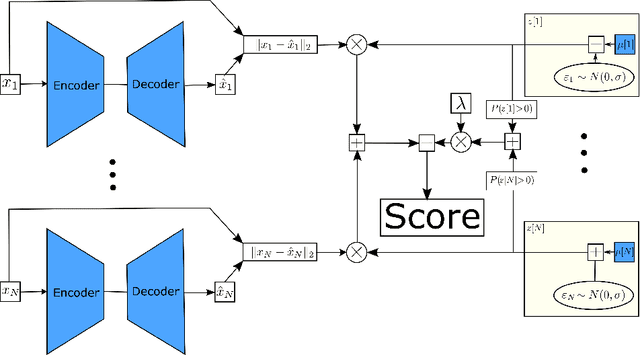
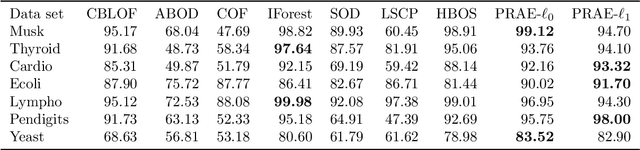
Empirical observations often consist of anomalies (or outliers) that contaminate the data. Accurate identification of anomalous samples is crucial for the success of downstream data analysis tasks. To automatically identify anomalies, we propose a new type of autoencoder (AE) which we term Probabilistic Robust autoencoder (PRAE). PRAE is designed to simultaneously remove outliers and identify a low-dimensional representation for the inlier samples. We first describe Robust AE (RAE) as a model that aims to split the data to inlier samples from which a low dimensional representation is learned via an AE, and anomalous (outlier) samples that are excluded as they do not fit the low dimensional representation. Robust AE minimizes the reconstruction of the AE while attempting to incorporate as many observations as possible. This could be realized by subtracting from the reconstruction term an $\ell_0$ norm counting the number of selected observations. Since the $\ell_0$ norm is not differentiable, we propose two probabilistic relaxations for the RAE approach and demonstrate that they can effectively identify anomalies. We prove that the solution to PRAE is equivalent to the solution of RAE and demonstrate using extensive simulations that PRAE is at par with state-of-the-art methods for anomaly detection.

Non-Parametric Estimation of Manifolds from Noisy Data

A common observation in data-driven applications is that high dimensional data has a low intrinsic dimension, at least locally. In this work, we consider the problem of estimating a $d$ dimensional sub-manifold of $\mathbb{R}^D$ from a finite set of noisy samples. Assuming that the data was sampled uniformly from a tubular neighborhood of $\mathcal{M}\in \mathcal{C}^k$, a compact manifold without boundary, we present an algorithm that takes a point $r$ from the tubular neighborhood and outputs $\hat p_n\in \mathbb{R}^D$, and $\widehat{T_{\hat p_n}\mathcal{M}}$ an element in the Grassmanian $Gr(d, D)$. We prove that as the number of samples $n\to\infty$ the point $\hat p_n$ converges to $p\in \mathcal{M}$ and $\widehat{T_{\hat p_n}\mathcal{M}}$ converges to $T_p\mathcal{M}$ (the tangent space at that point) with high probability. Furthermore, we show that the estimation yields asymptotic rates of convergence of $n^{-\frac{k}{2k + d}}$ for the point estimation and $n^{-\frac{k-1}{2k + d}}$ for the estimation of the tangent space. These rates are known to be optimal for the case of function estimation.

Spectral Top-Down Recovery of Latent Tree Models

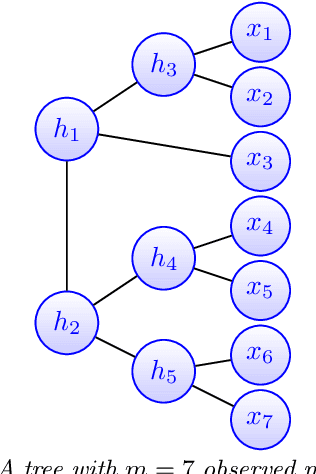
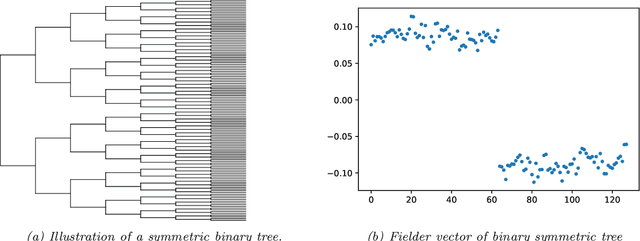
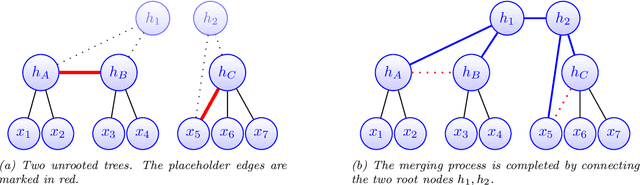
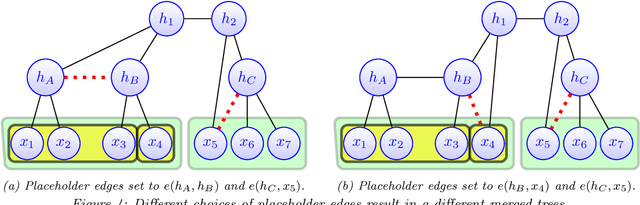
Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.

Approximation of Functions over Manifolds: A Moving Least-Squares Approach

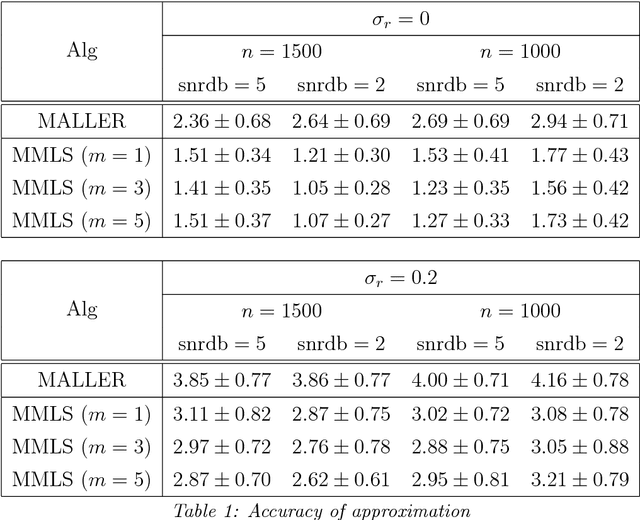
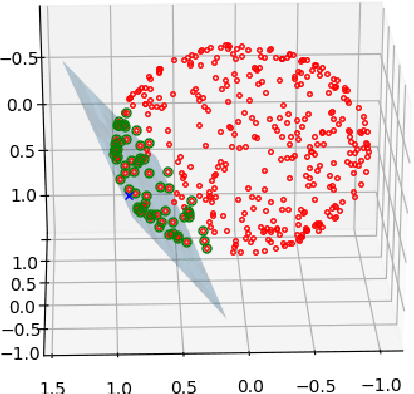
We present an algorithm for approximating a function defined over a $d$-dimensional manifold utilizing only noisy function values at locations sampled from the manifold with noise. To produce the approximation we do not require any knowledge regarding the manifold other than its dimension $d$. The approximation scheme is based upon the Manifold Moving Least-Squares (MMLS). The proposed algorithm is resistant to noise in both the domain and function values. Furthermore, the approximant is shown to be smooth and of approximation order of $\mathcal{O}(h^{m+1})$ for non-noisy data, where $h$ is the mesh size with respect to the manifold domain, and $m$ is the degree of a local polynomial approximation utilized in our algorithm. In addition, the proposed algorithm is linear in time with respect to the ambient-space's dimension. Thus, in case of extremely large ambient space dimension, we are able to avoid the curse of dimensionality without having to perform non-linear dimension reduction, which introduces distortions to the manifold data. Using numerical experiments, we compare the presented method to state-of-the-art algorithms for regression over manifolds and show its potential.

Similarity Search Over Graphs Using Localized Spectral Analysis

This paper provides a new similarity detection algorithm. Given an input set of multi-dimensional data points, where each data point is assumed to be multi-dimensional, and an additional reference data point for similarity finding, the algorithm uses kernel method that embeds the data points into a low dimensional manifold. Unlike other kernel methods, which consider the entire data for the embedding, our method selects a specific set of kernel eigenvectors. The eigenvectors are chosen to separate between the data points and the reference data point so that similar data points can be easily identified as being distinct from most of the members in the dataset.

A max-cut approach to heterogeneity in cryo-electron microscopy

The field of cryo-electron microscopy has made astounding advancements in the past few years, mainly due to improvements in the hardware of the microscopes. Yet, one of the key open challenges of the field remains the processing of heterogeneous data sets, produced from samples containing particles at several different conformational states. For such data sets, one must first classify their images into homogeneous groups, where each group corresponds to the same underlying structure, followed by reconstruction of a three-dimensional model from each of the homogeneous groups. This task has been proven to be extremely difficult. In this paper we present an iterative algorithm for processing heterogeneous data sets that combines the classification and reconstruction steps. We prove accuracy and stability bounds on the algorithm, and demonstrate it on simulated as well as experimental data sets.

PCA-Based Out-of-Sample Extension for Dimensionality Reduction

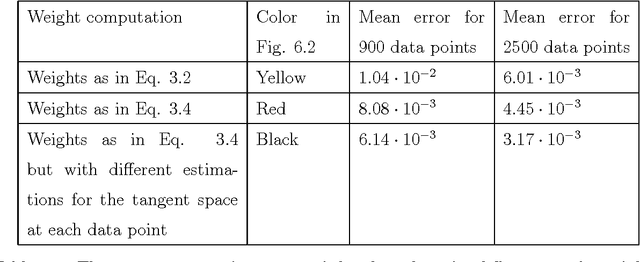
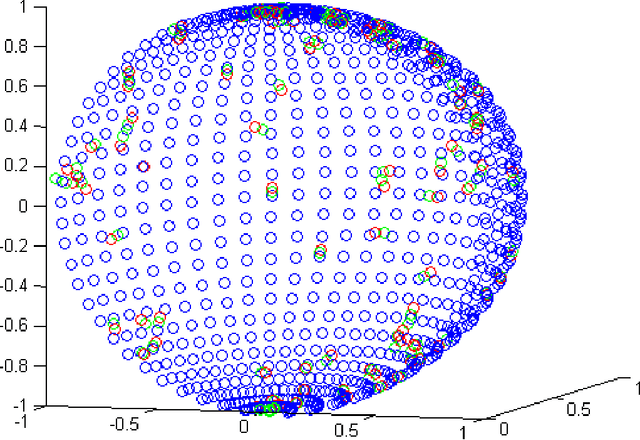
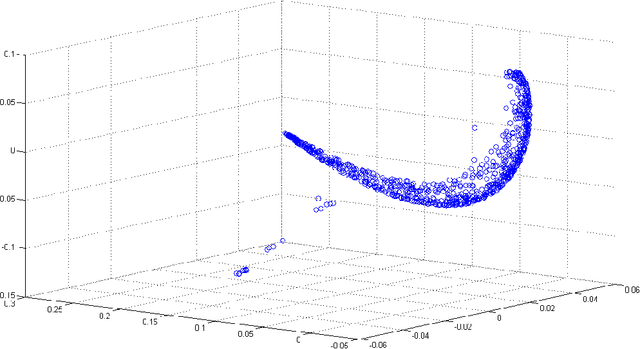
Dimensionality reduction methods are very common in the field of high dimensional data analysis. Typically, algorithms for dimensionality reduction are computationally expensive. Therefore, their applications for the analysis of massive amounts of data are impractical. For example, repeated computations due to accumulated data are computationally prohibitive. In this paper, an out-of-sample extension scheme, which is used as a complementary method for dimensionality reduction, is presented. We describe an algorithm which performs an out-of-sample extension to newly-arrived data points. Unlike other extension algorithms such as Nystr\"om algorithm, the proposed algorithm uses the intrinsic geometry of the data and properties for dimensionality reduction map. We prove that the error of the proposed algorithm is bounded. Additionally to the out-of-sample extension, the algorithm provides a degree of the abnormality of any newly-arrived data point.