Graph-Based Automatic Feature Selection for Multi-Class Classification via Mean Simplified Silhouette

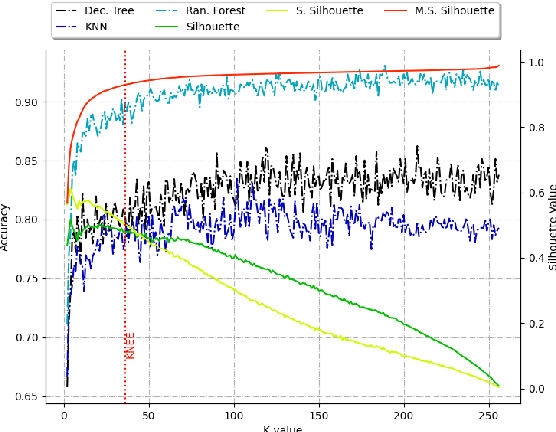
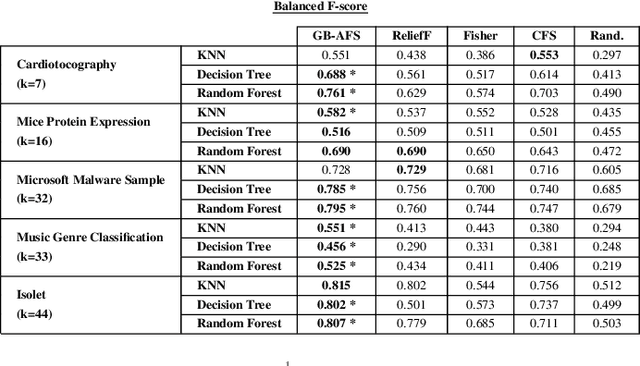
This paper introduces a novel graph-based filter method for automatic feature selection (abbreviated as GB-AFS) for multi-class classification tasks. The method determines the minimum combination of features required to sustain prediction performance while maintaining complementary discriminating abilities between different classes. It does not require any user-defined parameters such as the number of features to select. The methodology employs the Jeffries-Matusita (JM) distance in conjunction with t-distributed Stochastic Neighbor Embedding (t-SNE) to generate a low-dimensional space reflecting how effectively each feature can differentiate between each pair of classes. The minimum number of features is selected using our newly developed Mean Simplified Silhouette (abbreviated as MSS) index, designed to evaluate the clustering results for the feature selection task. Experimental results on public data sets demonstrate the superior performance of the proposed GB-AFS over other filter-based techniques and automatic feature selection approaches. Moreover, the proposed algorithm maintained the accuracy achieved when utilizing all features, while using only $7\%$ to $30\%$ of the features. Consequently, this resulted in a reduction of the time needed for classifications, from $15\%$ to $70\%$.

Approximation of Functions over Manifolds: A Moving Least-Squares Approach

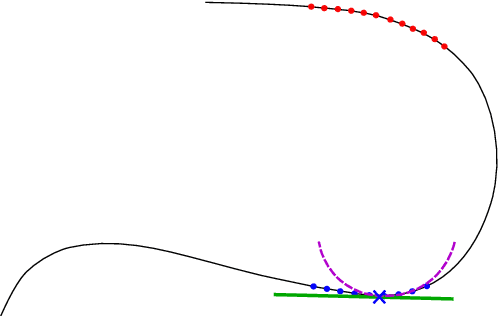
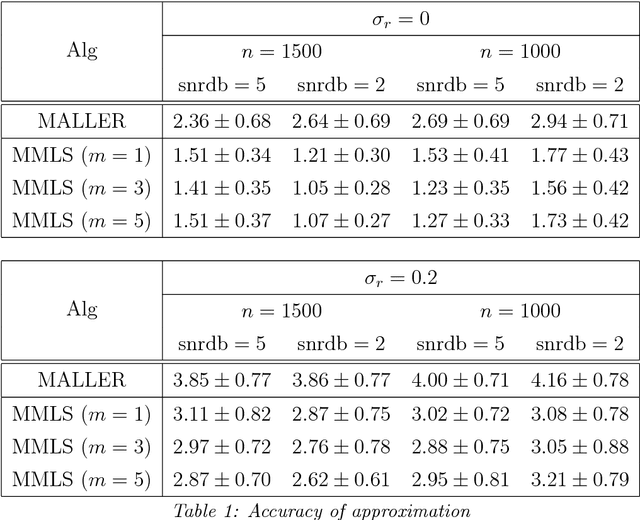
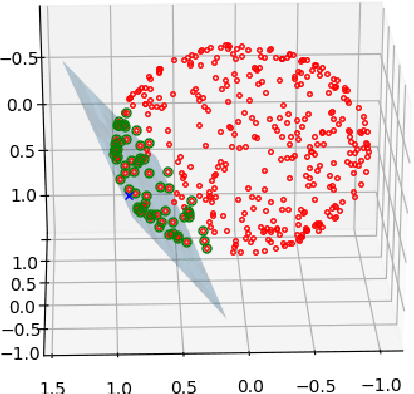
We present an algorithm for approximating a function defined over a $d$-dimensional manifold utilizing only noisy function values at locations sampled from the manifold with noise. To produce the approximation we do not require any knowledge regarding the manifold other than its dimension $d$. The approximation scheme is based upon the Manifold Moving Least-Squares (MMLS). The proposed algorithm is resistant to noise in both the domain and function values. Furthermore, the approximant is shown to be smooth and of approximation order of $\mathcal{O}(h^{m+1})$ for non-noisy data, where $h$ is the mesh size with respect to the manifold domain, and $m$ is the degree of a local polynomial approximation utilized in our algorithm. In addition, the proposed algorithm is linear in time with respect to the ambient-space's dimension. Thus, in case of extremely large ambient space dimension, we are able to avoid the curse of dimensionality without having to perform non-linear dimension reduction, which introduces distortions to the manifold data. Using numerical experiments, we compare the presented method to state-of-the-art algorithms for regression over manifolds and show its potential.

Manifold Approximation by Moving Least-Squares Projection (MMLS)

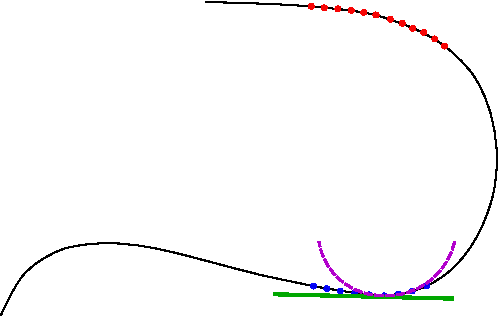
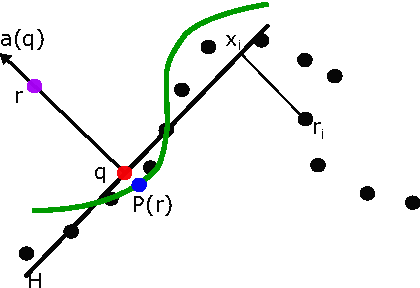
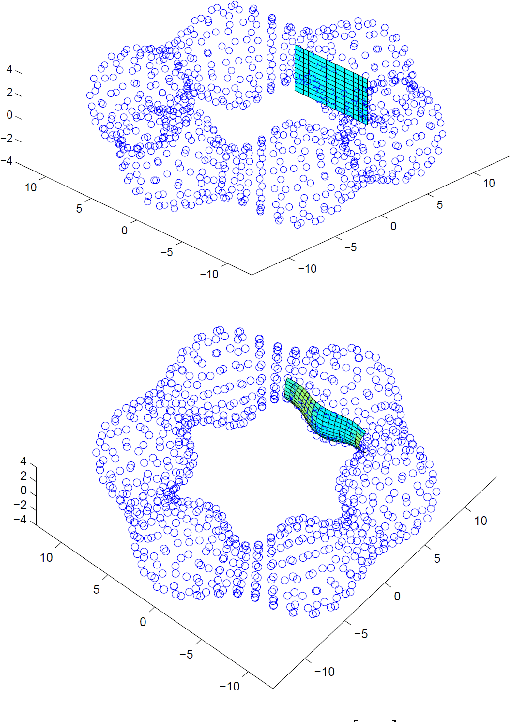
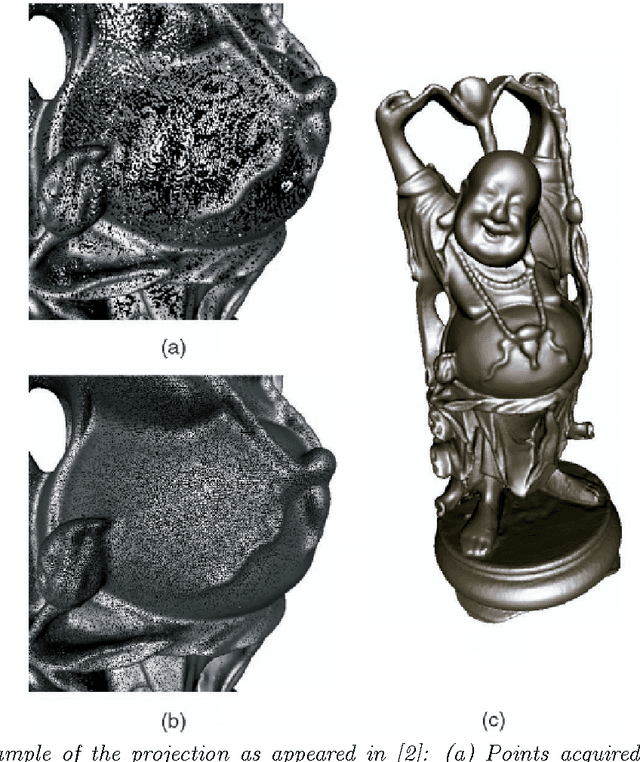
In order to avoid the curse of dimensionality, frequently encountered in Big Data analysis, there was a vast development in the field of linear and nonlinear dimension reduction techniques in recent years. These techniques (sometimes referred to as manifold learning) assume that the scattered input data is lying on a lower dimensional manifold, thus the high dimensionality problem can be overcome by learning the lower dimensionality behavior. However, in real life applications, data is often very noisy. In this work, we propose a method to approximate $\MM$ a $d$-dimensional $C^{m+1}$ smooth submanifold of $\RR^n$ ($d << n$) based upon noisy scattered data points (i.e., a data cloud). We assume that the data points are located "near" the lower dimensional manifold and suggest a non-linear moving least-squares projection on an approximating $d$-dimensional manifold. Under some mild assumptions, the resulting approximant is shown to be infinitely smooth and of high approximation order (i.e., $O(h^{m+1})$, where $h$ is the fill distance and $m$ is the degree of the local polynomial approximation). The method presented here assumes no analytic knowledge of the approximated manifold and the approximation algorithm is linear in the large dimension $n$. Furthermore, the approximating manifold can serve as a framework to perform operations directly on the high dimensional data in a computationally efficient manner. This way, the preparatory step of dimension reduction, which induces distortions to the data, can be avoided altogether.

Computer Aided Restoration of Handwritten Character Strokes

This work suggests a new variational approach to the task of computer aided restoration of incomplete characters, residing in a highly noisy document. We model character strokes as the movement of a pen with a varying radius. Following this model, a cubic spline representation is being utilized to perform gradient descent steps, while maintaining interpolation at some initial (manually sampled) points. The proposed algorithm was utilized in the process of restoring approximately 1000 ancient Hebrew characters (dating to ca. 8th-7th century BCE), some of which are presented herein and show that the algorithm yields plausible results when applied on deteriorated documents.