Modeling Latent Neural Dynamics with Gaussian Process Switching Linear Dynamical Systems

Understanding how the collective activity of neural populations relates to computation and ultimately behavior is a key goal in neuroscience. To this end, statistical methods which describe high-dimensional neural time series in terms of low-dimensional latent dynamics have played a fundamental role in characterizing neural systems. Yet, what constitutes a successful method involves two opposing criteria: (1) methods should be expressive enough to capture complex nonlinear dynamics, and (2) they should maintain a notion of interpretability often only warranted by simpler linear models. In this paper, we develop an approach that balances these two objectives: the Gaussian Process Switching Linear Dynamical System (gpSLDS). Our method builds on previous work modeling the latent state evolution via a stochastic differential equation whose nonlinear dynamics are described by a Gaussian process (GP-SDEs). We propose a novel kernel function which enforces smoothly interpolated locally linear dynamics, and therefore expresses flexible -- yet interpretable -- dynamics akin to those of recurrent switching linear dynamical systems (rSLDS). Our approach resolves key limitations of the rSLDS such as artifactual oscillations in dynamics near discrete state boundaries, while also providing posterior uncertainty estimates of the dynamics. To fit our models, we leverage a modified learning objective which improves the estimation accuracy of kernel hyperparameters compared to previous GP-SDE fitting approaches. We apply our method to synthetic data and data recorded in two neuroscience experiments and demonstrate favorable performance in comparison to the rSLDS.

Spectral Top-Down Recovery of Latent Tree Models

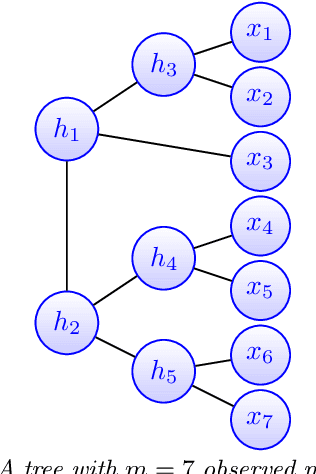
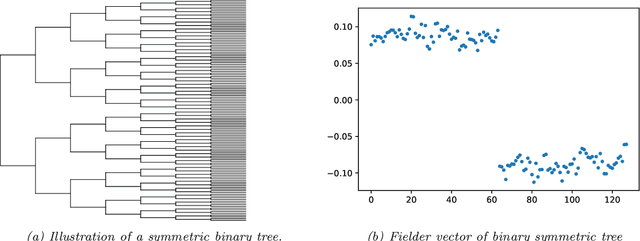
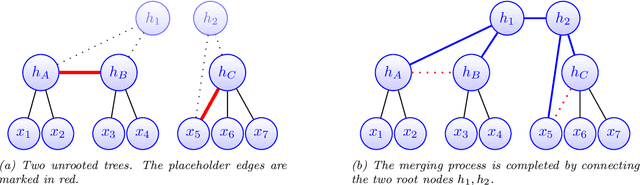
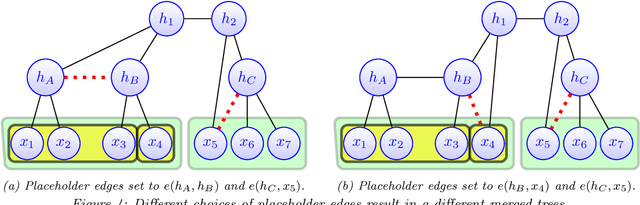
Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.