Joseph T. Chang
Spectral Top-Down Recovery of Latent Tree Models
Feb 26, 2021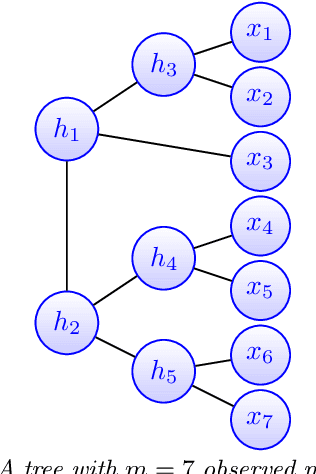
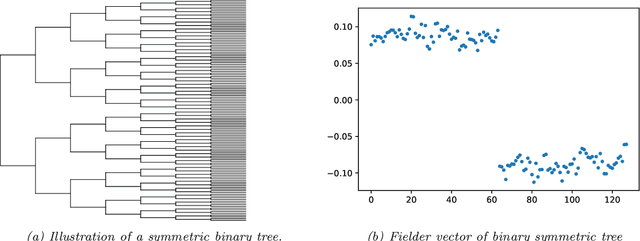
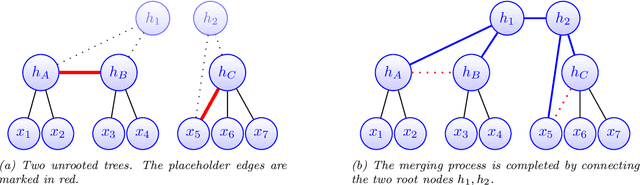
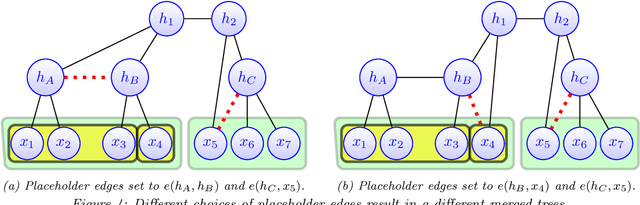
Abstract:Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.
Spectral neighbor joining for reconstruction of latent tree models
Feb 28, 2020
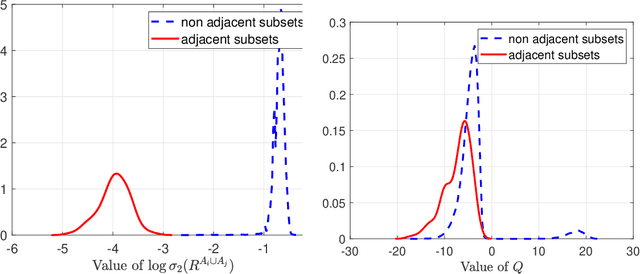
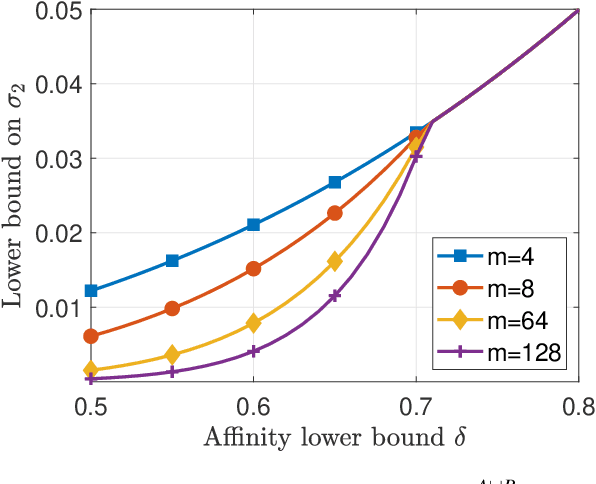
Abstract:A key assumption in multiple scientific applications is that the distribution of observed data can be modeled by a latent tree graphical model. An important example is phylogenetics, where the tree models the evolutionary lineages of various organisms. Given a set of independent realizations of the random variables at the leaves of the tree, a common task is to infer the underlying tree topology. In this work we develop Spectral Neighbor Joining (SNJ), a novel method to recover latent tree graphical models. In contrast to distance based methods, SNJ is based on a spectral measure of similarity between all pairs of observed variables. We prove that SNJ is consistent, and derive a sufficient condition for correct tree recovery from an estimated similarity matrix. Combining this condition with a concentration of measure result on the similarity matrix, we bound the number of samples required to recover the tree with high probability. We illustrate via extensive simulations that SNJ requires fewer samples to accurately recover trees in regimes where the tree contains a large number of leaves or long edges. We provide theoretical support for this observation by analyzing the model of a perfect binary tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge