Ariel Jaffe
Spectral Self-supervised Feature Selection
Jul 12, 2024Abstract:Choosing a meaningful subset of features from high-dimensional observations in unsupervised settings can greatly enhance the accuracy of downstream analysis, such as clustering or dimensionality reduction, and provide valuable insights into the sources of heterogeneity in a given dataset. In this paper, we propose a self-supervised graph-based approach for unsupervised feature selection. Our method's core involves computing robust pseudo-labels by applying simple processing steps to the graph Laplacian's eigenvectors. The subset of eigenvectors used for computing pseudo-labels is chosen based on a model stability criterion. We then measure the importance of each feature by training a surrogate model to predict the pseudo-labels from the observations. Our approach is shown to be robust to challenging scenarios, such as the presence of outliers and complex substructures. We demonstrate the effectiveness of our method through experiments on real-world datasets, showing its robustness across multiple domains, particularly its effectiveness on biological datasets.
Multi-modal Differentiable Unsupervised Feature Selection
Mar 16, 2023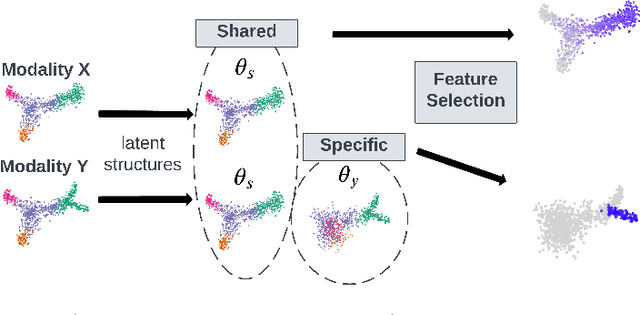
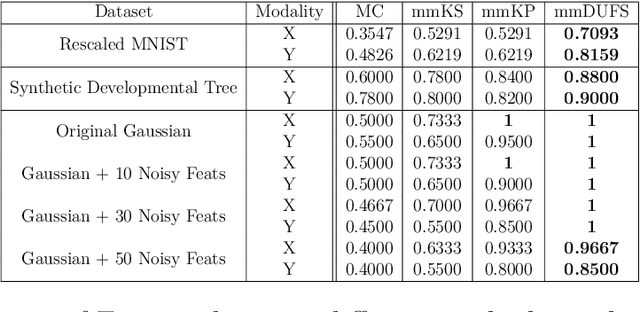
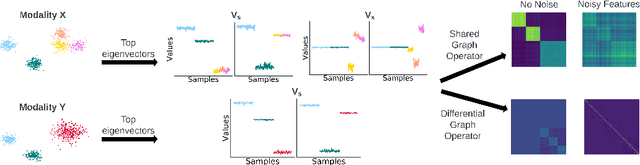
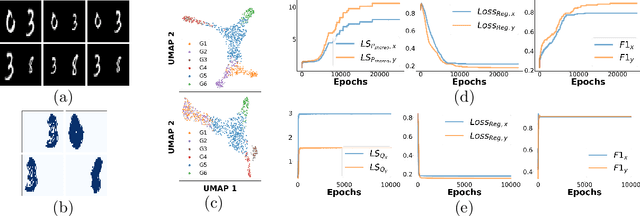
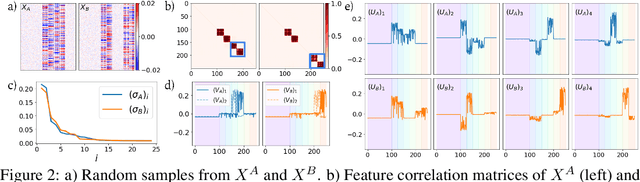
Abstract:Multi-modal high throughput biological data presents a great scientific opportunity and a significant computational challenge. In multi-modal measurements, every sample is observed simultaneously by two or more sets of sensors. In such settings, many observed variables in both modalities are often nuisance and do not carry information about the phenomenon of interest. Here, we propose a multi-modal unsupervised feature selection framework: identifying informative variables based on coupled high-dimensional measurements. Our method is designed to identify features associated with two types of latent low-dimensional structures: (i) shared structures that govern the observations in both modalities and (ii) differential structures that appear in only one modality. To that end, we propose two Laplacian-based scoring operators. We incorporate the scores with differentiable gates that mask nuisance features and enhance the accuracy of the structure captured by the graph Laplacian. The performance of the new scheme is illustrated using synthetic and real datasets, including an extended biological application to single-cell multi-omics.
DiSC: Differential Spectral Clustering of Features
Nov 10, 2022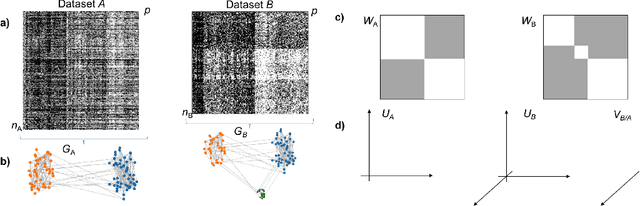


Abstract:Selecting subsets of features that differentiate between two conditions is a key task in a broad range of scientific domains. In many applications, the features of interest form clusters with similar effects on the data at hand. To recover such clusters we develop DiSC, a data-driven approach for detecting groups of features that differentiate between conditions. For each condition, we construct a graph whose nodes correspond to the features and whose weights are functions of the similarity between them for that condition. We then apply a spectral approach to compute subsets of nodes whose connectivity differs significantly between the condition-specific feature graphs. On the theoretical front, we analyze our approach with a toy example based on the stochastic block model. We evaluate DiSC on a variety of datasets, including MNIST, hyperspectral imaging, simulated scRNA-seq and task fMRI, and demonstrate that DiSC uncovers features that better differentiate between conditions compared to competing methods.
Weakly Supervised Indoor Localization via Manifold Matching
Feb 07, 2022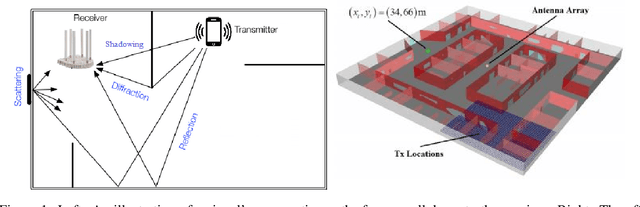
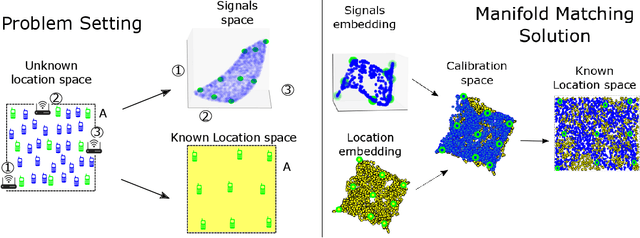
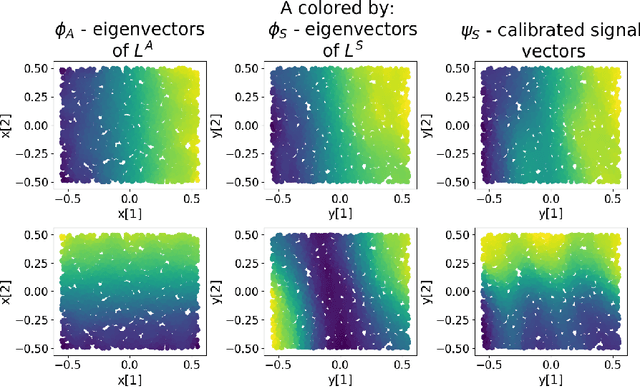
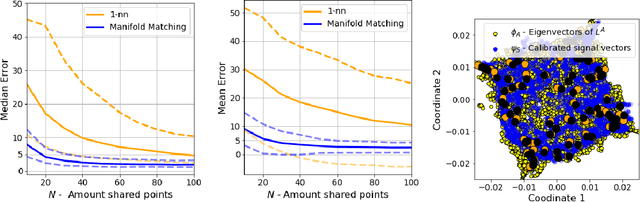
Abstract:Inferring the location of a mobile device in an indoor setting is an open problem of utmost significance. A leading approach that does not require the deployment of expensive infrastructure is fingerprinting, where a classifier is trained to predict the location of a device based on its captured signal. The main caveat of this approach is that acquiring a sufficiently large and accurate training set may be prohibitively expensive. Here, we propose a weakly supervised method that only requires the location of a small number of devices. The localization is done by matching a low-dimensional spectral representation of the signals to a given sketch of the indoor environment. We test our approach on simulated and real data and show that it yields an accuracy of a few meters, which is on par with fully supervised approaches. The simplicity of our method and its accuracy with minimal supervision makes it ideal for implementation in indoor localization systems.
Spectral Top-Down Recovery of Latent Tree Models
Feb 26, 2021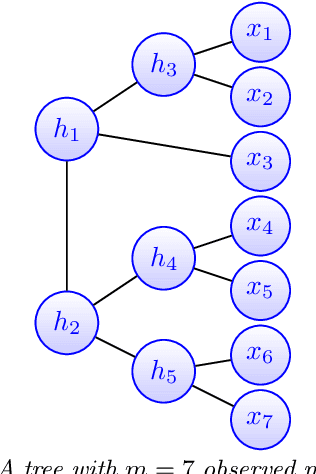
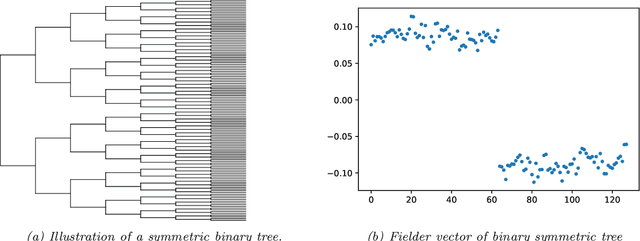
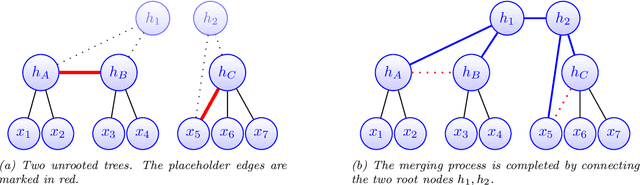
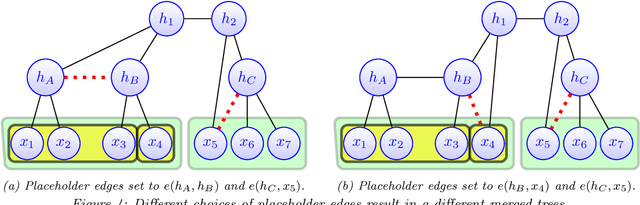
Abstract:Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.
Spectral neighbor joining for reconstruction of latent tree models
Feb 28, 2020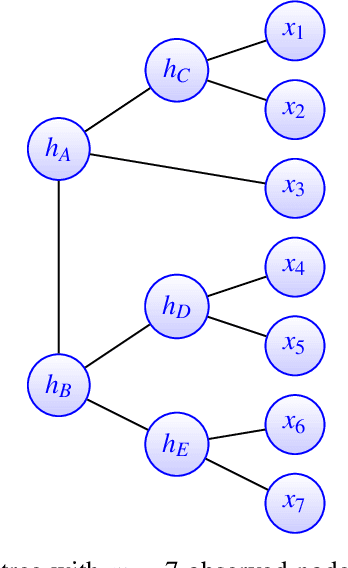
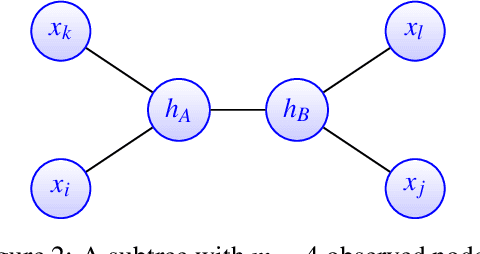
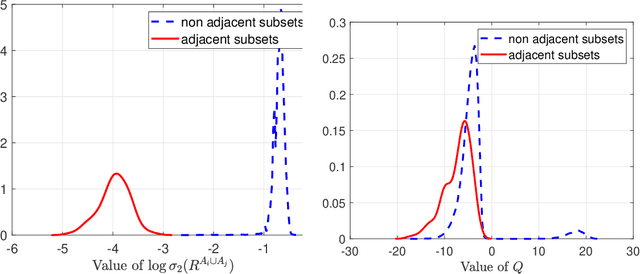
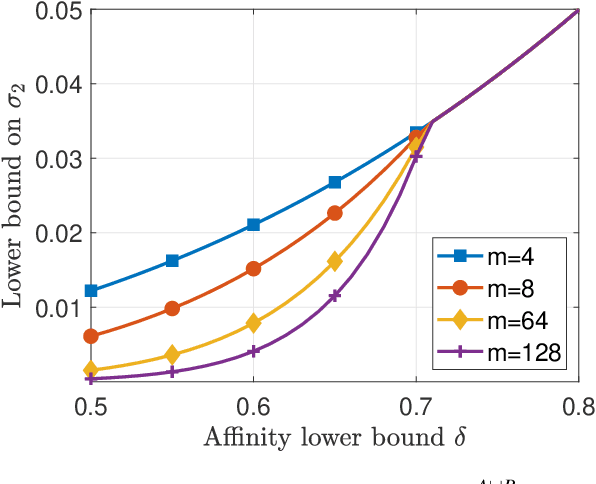
Abstract:A key assumption in multiple scientific applications is that the distribution of observed data can be modeled by a latent tree graphical model. An important example is phylogenetics, where the tree models the evolutionary lineages of various organisms. Given a set of independent realizations of the random variables at the leaves of the tree, a common task is to infer the underlying tree topology. In this work we develop Spectral Neighbor Joining (SNJ), a novel method to recover latent tree graphical models. In contrast to distance based methods, SNJ is based on a spectral measure of similarity between all pairs of observed variables. We prove that SNJ is consistent, and derive a sufficient condition for correct tree recovery from an estimated similarity matrix. Combining this condition with a concentration of measure result on the similarity matrix, we bound the number of samples required to recover the tree with high probability. We illustrate via extensive simulations that SNJ requires fewer samples to accurately recover trees in regimes where the tree contains a large number of leaves or long edges. We provide theoretical support for this observation by analyzing the model of a perfect binary tree.
The Spectral Underpinning of word2vec
Feb 27, 2020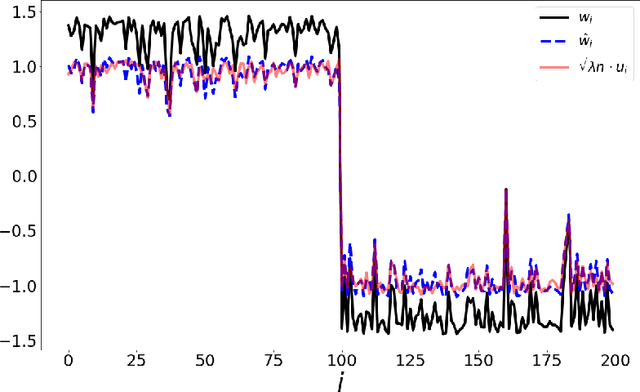
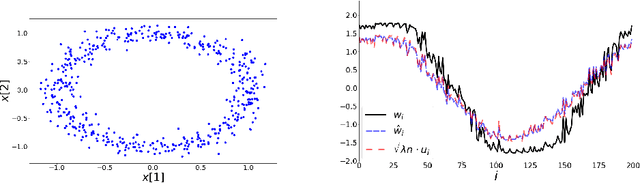
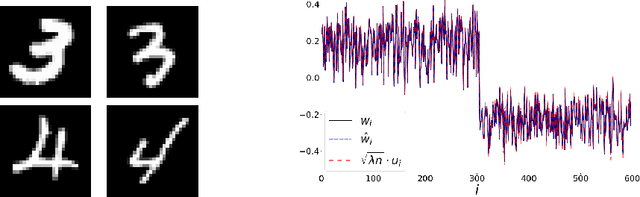
Abstract:word2vec due to Mikolov \textit{et al.} (2013) is a word embedding method that is widely used in natural language processing. Despite its great success and frequent use, theoretical justification is still lacking. The main contribution of our paper is to propose a rigorous analysis of the highly nonlinear functional of word2vec. Our results suggest that word2vec may be primarily driven by an underlying spectral method. This insight may open the door to obtaining provable guarantees for word2vec. We support these findings by numerical simulations. One fascinating open question is whether the nonlinear properties of word2vec that are not captured by the spectral method are beneficial and, if so, by what mechanism.
Learning Binary Latent Variable Models: A Tensor Eigenpair Approach
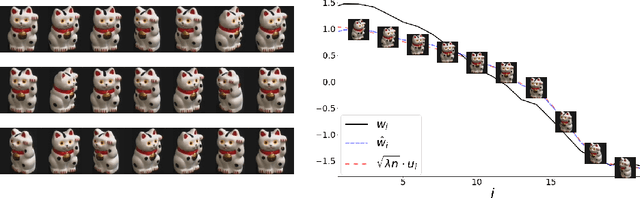
Feb 27, 2018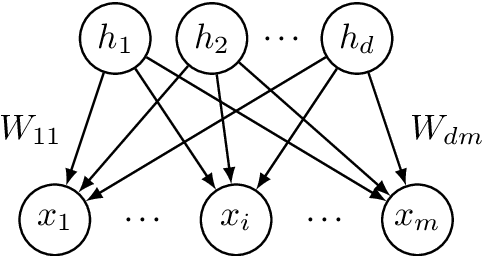
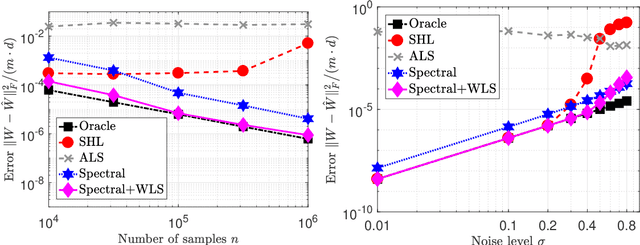
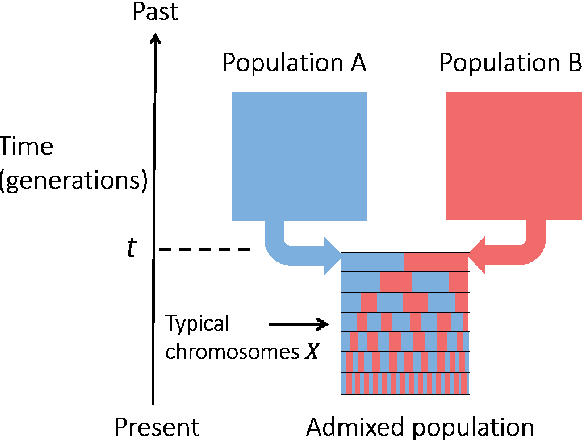
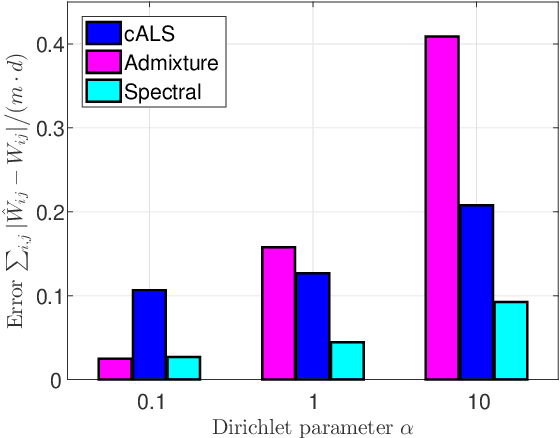
Abstract:Latent variable models with hidden binary units appear in various applications. Learning such models, in particular in the presence of noise, is a challenging computational problem. In this paper we propose a novel spectral approach to this problem, based on the eigenvectors of both the second order moment matrix and third order moment tensor of the observed data. We prove that under mild non-degeneracy conditions, our method consistently estimates the model parameters at the optimal parametric rate. Our tensor-based method generalizes previous orthogonal tensor decomposition approaches, where the hidden units were assumed to be either statistically independent or mutually exclusive. We illustrate the consistency of our method on simulated data and demonstrate its usefulness in learning a common model for population mixtures in genetics.
Minimax-optimal semi-supervised regression on unknown manifolds
Mar 06, 2017
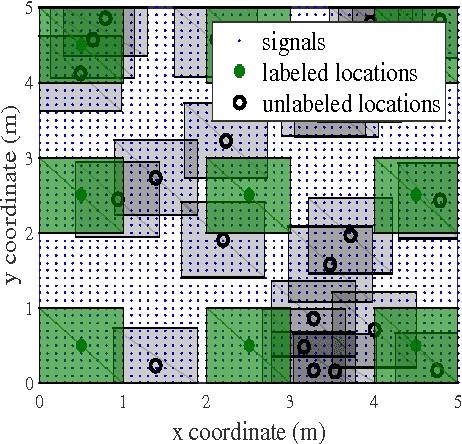
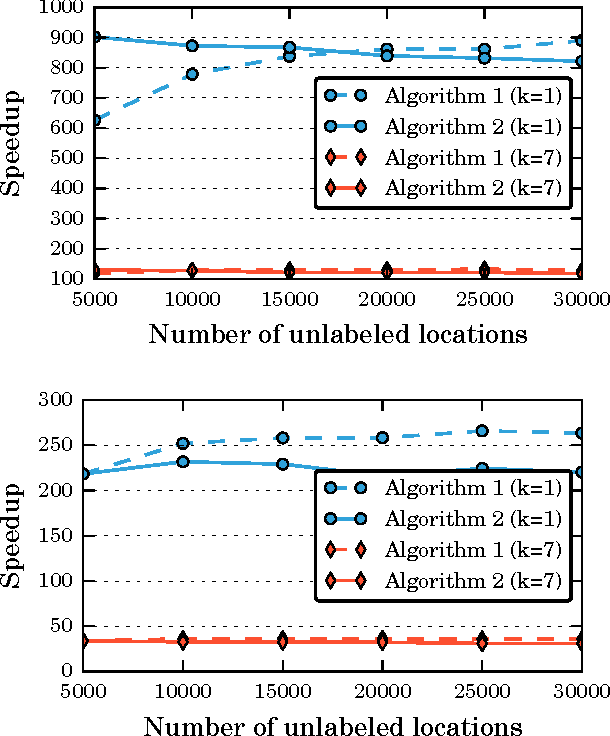
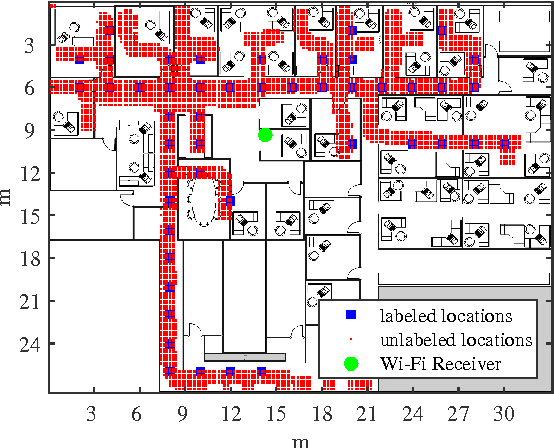
Abstract:We consider semi-supervised regression when the predictor variables are drawn from an unknown manifold. A simple two step approach to this problem is to: (i) estimate the manifold geodesic distance between any pair of points using both the labeled and unlabeled instances; and (ii) apply a k nearest neighbor regressor based on these distance estimates. We prove that given sufficiently many unlabeled points, this simple method of geodesic kNN regression achieves the optimal finite-sample minimax bound on the mean squared error, as if the manifold were known. Furthermore, we show how this approach can be efficiently implemented, requiring only O(k N log N) operations to estimate the regression function at all N labeled and unlabeled points. We illustrate this approach on two datasets with a manifold structure: indoor localization using WiFi fingerprints and facial pose estimation. In both cases, geodesic kNN is more accurate and much faster than the popular Laplacian eigenvector regressor.
Unsupervised Ensemble Learning with Dependent Classifiers
Feb 23, 2016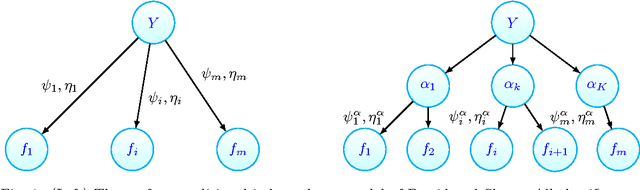
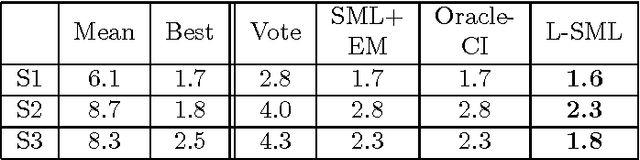
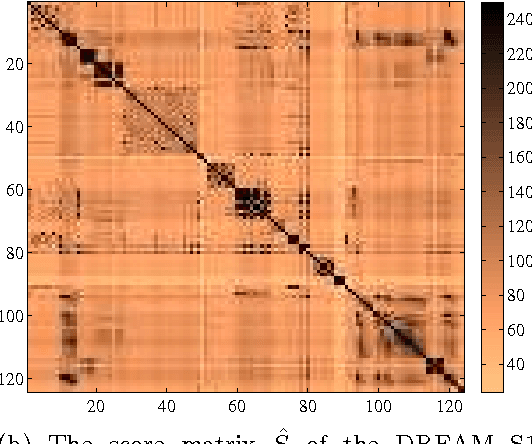

Abstract:In unsupervised ensemble learning, one obtains predictions from multiple sources or classifiers, yet without knowing the reliability and expertise of each source, and with no labeled data to assess it. The task is to combine these possibly conflicting predictions into an accurate meta-learner. Most works to date assumed perfect diversity between the different sources, a property known as conditional independence. In realistic scenarios, however, this assumption is often violated, and ensemble learners based on it can be severely sub-optimal. The key challenges we address in this paper are:\ (i) how to detect, in an unsupervised manner, strong violations of conditional independence; and (ii) construct a suitable meta-learner. To this end we introduce a statistical model that allows for dependencies between classifiers. Our main contributions are the development of novel unsupervised methods to detect strongly dependent classifiers, better estimate their accuracies, and construct an improved meta-learner. Using both artificial and real datasets, we showcase the importance of taking classifier dependencies into account and the competitive performance of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge