Minimax-optimal semi-supervised regression on unknown manifolds
Paper and Code
Mar 06, 2017
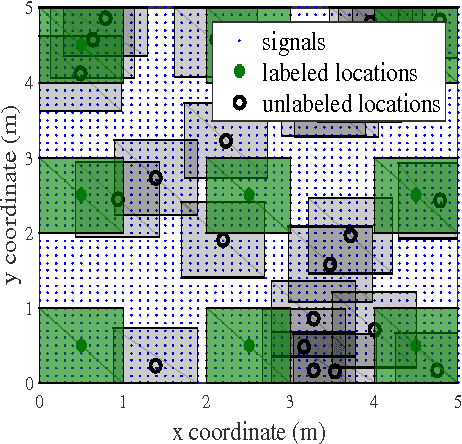
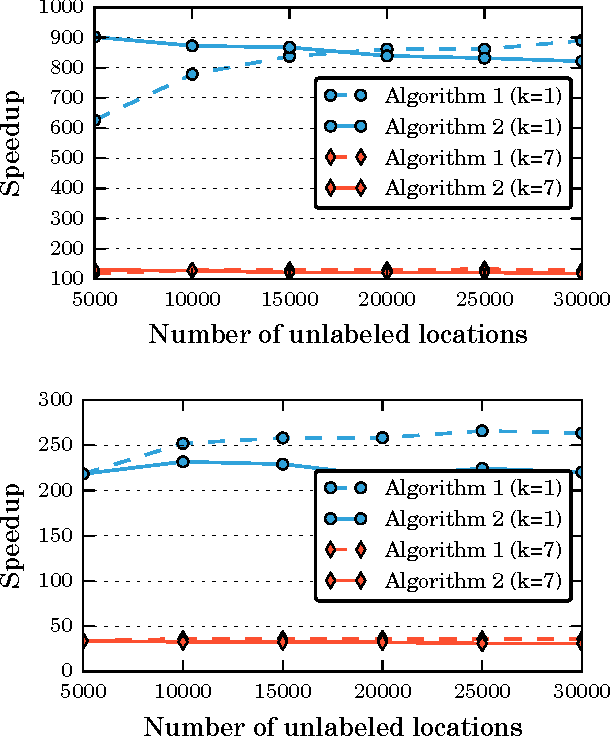
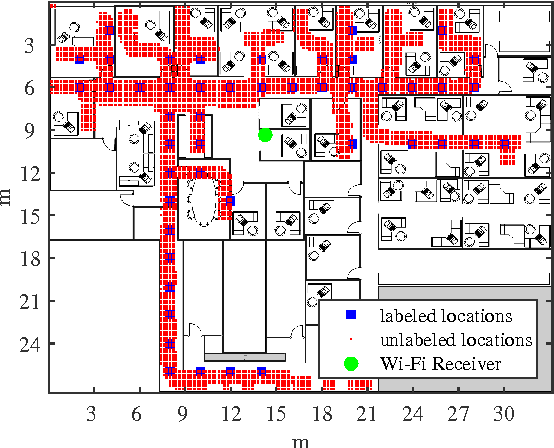
We consider semi-supervised regression when the predictor variables are drawn from an unknown manifold. A simple two step approach to this problem is to: (i) estimate the manifold geodesic distance between any pair of points using both the labeled and unlabeled instances; and (ii) apply a k nearest neighbor regressor based on these distance estimates. We prove that given sufficiently many unlabeled points, this simple method of geodesic kNN regression achieves the optimal finite-sample minimax bound on the mean squared error, as if the manifold were known. Furthermore, we show how this approach can be efficiently implemented, requiring only O(k N log N) operations to estimate the regression function at all N labeled and unlabeled points. We illustrate this approach on two datasets with a manifold structure: indoor localization using WiFi fingerprints and facial pose estimation. In both cases, geodesic kNN is more accurate and much faster than the popular Laplacian eigenvector regressor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge