Manifold learning with arbitrary norms

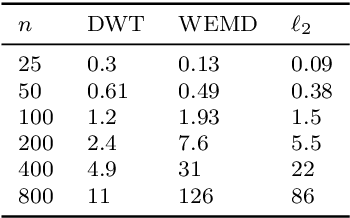
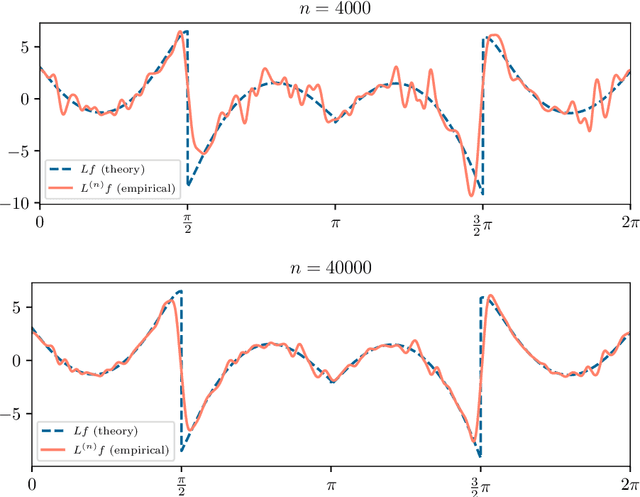
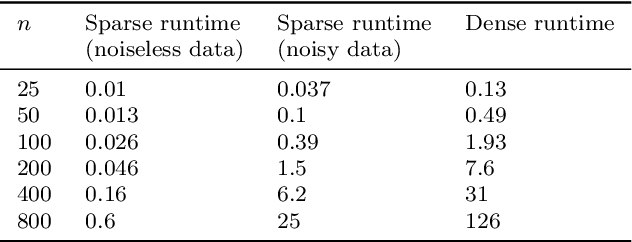
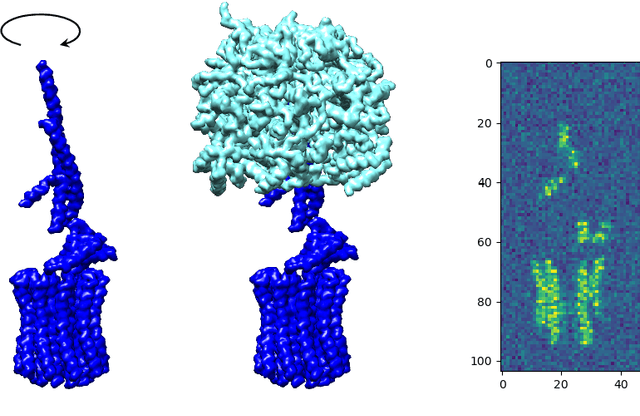
Manifold learning methods play a prominent role in nonlinear dimensionality reduction and other tasks involving high-dimensional data sets with low intrinsic dimensionality. Many of these methods are graph-based: they associate a vertex with each data point and a weighted edge between each pair of close points. Existing theory shows, under certain conditions, that the Laplacian matrix of the constructed graph converges to the Laplace-Beltrami operator of the data manifold. However, this result assumes the Euclidean norm is used for measuring distances. In this paper, we determine the limiting differential operator for graph Laplacians constructed using $\textit{any}$ norm. The proof involves a subtle interplay between the second fundamental form of the underlying manifold and the convex geometry of the norm's unit ball. To motivate the use of non-Euclidean norms, we show in a numerical simulation that manifold learning based on Earthmover's distances outperforms the standard Euclidean variant for learning molecular shape spaces, in terms of both sample complexity and computational complexity.

Wasserstein K-Means for Clustering Tomographic Projections

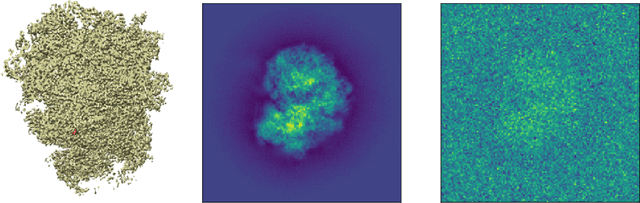
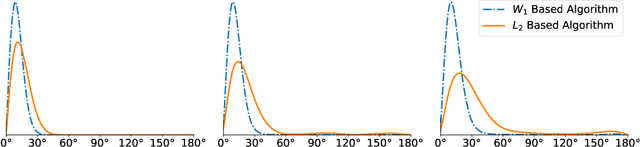
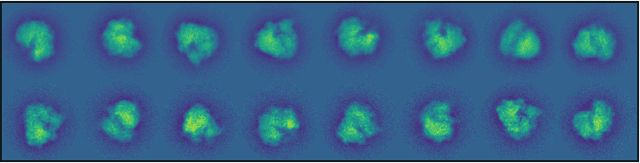
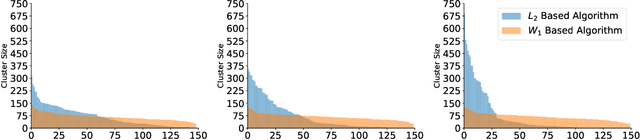
Motivated by the 2D class averaging problem in single-particle cryo-electron microscopy (cryo-EM), we present a k-means algorithm based on a rotationally-invariant Wasserstein metric for images. Unlike existing methods that are based on Euclidean ($L_2$) distances, we prove that the Wasserstein metric better accommodates for the out-of-plane angular differences between different particle views. We demonstrate on a synthetic dataset that our method gives superior results compared to an $L_2$ baseline. Furthermore, there is little computational overhead, thanks to the use of a fast linear-time approximation to the Wasserstein-1 metric, also known as the Earthmover's distance.

Product Manifold Learning

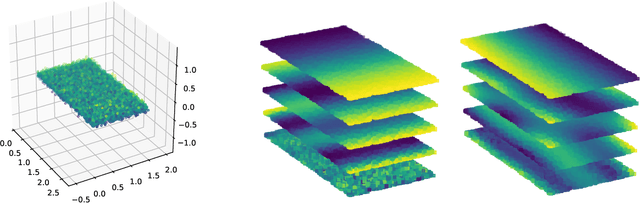
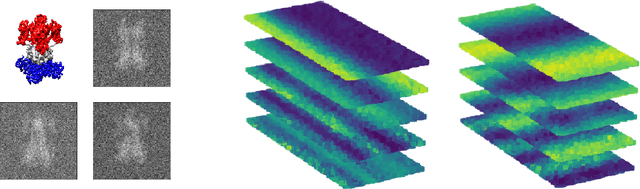
We consider problems of dimensionality reduction and learning data representations for continuous spaces with two or more independent degrees of freedom. Such problems occur, for example, when observing shapes with several components that move independently. Mathematically, if the parameter space of each continuous independent motion is a manifold, then their combination is known as a product manifold. In this paper, we present a new paradigm for non-linear independent component analysis called manifold factorization. Our factorization algorithm is based on spectral graph methods for manifold learning and the separability of the Laplacian operator on product spaces. Recovering the factors of a manifold yields meaningful lower-dimensional representations and provides a new way to focus on particular aspects of the data space while ignoring others. We demonstrate the potential use of our method for an important and challenging problem in structural biology: mapping the motions of proteins and other large molecules using cryo-electron microscopy datasets.

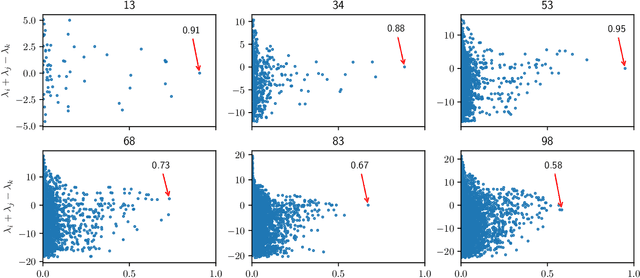
Unsupervised particle sorting for high-resolution single-particle cryo-EM

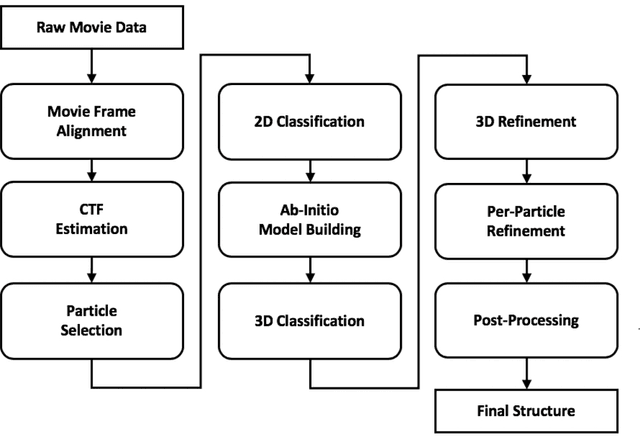
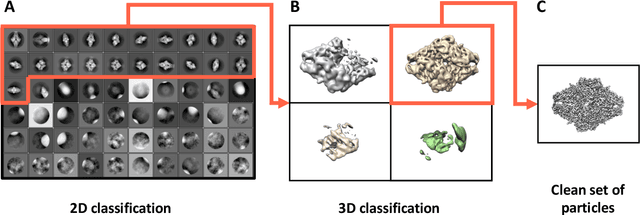
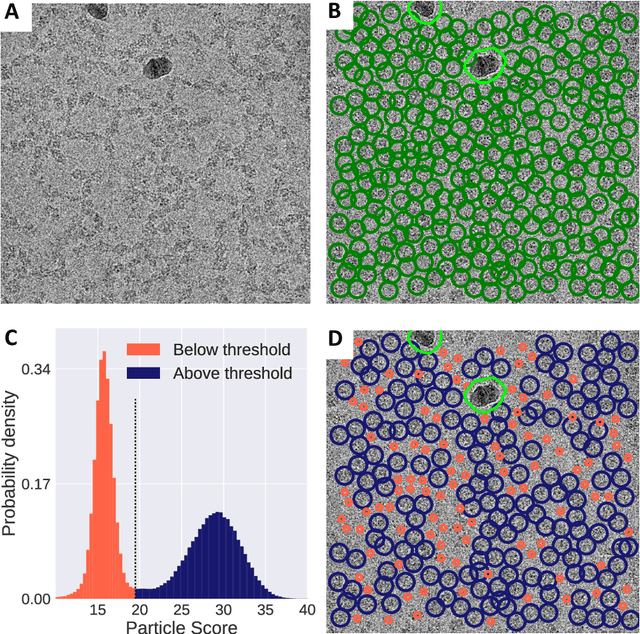
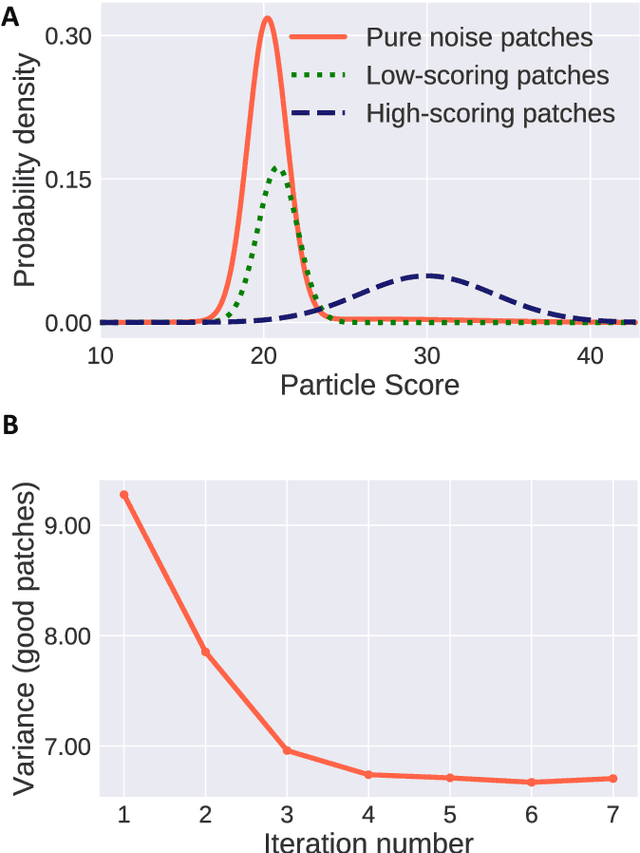
Single-particle cryo-Electron Microscopy (EM) has become a popular technique for determining the structure of challenging biomolecules that are inaccessible to other technologies. Recent advances in automation, both in data collection and data processing, have significantly lowered the barrier for non-expert users to successfully execute the structure determination workflow. Many critical data processing steps, however, still require expert user intervention in order to converge to the correct high-resolution structure. In particular, strategies to identify homogeneous populations of particles rely heavily on subjective criteria that are not always consistent or reproducible among different users. Here, we explore the use of unsupervised strategies for particle sorting that are compatible with the autonomous operation of the image processing pipeline. More specifically, we show that particles can be successfully sorted based on a simple statistical model for the distribution of scores assigned during refinement. This represents an important step towards the development of automated workflows for protein structure determination using single-particle cryo-EM.

Earthmover-based manifold learning for analyzing molecular conformation spaces

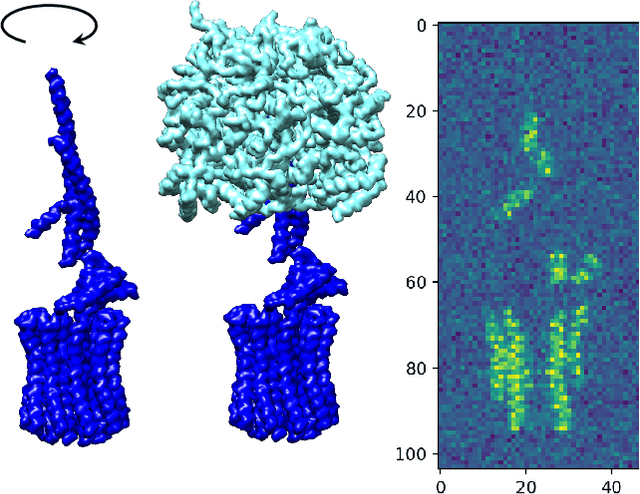
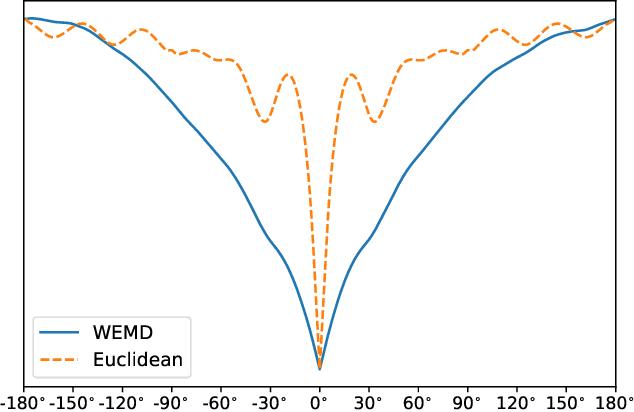
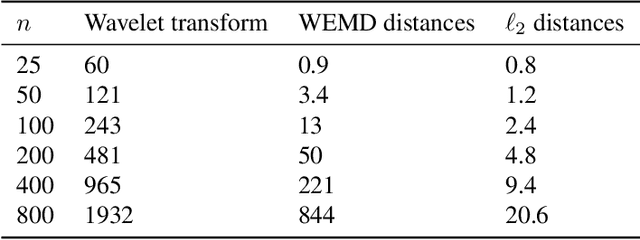
In this paper, we propose a novel approach for manifold learning that combines the Earthmover's distance (EMD) with the diffusion maps method for dimensionality reduction. We demonstrate the potential benefits of this approach for learning shape spaces of proteins and other flexible macromolecules using a simulated dataset of 3-D density maps that mimic the non-uniform rotary motion of ATP synthase. Our results show that EMD-based diffusion maps require far fewer samples to recover the intrinsic geometry than the standard diffusion maps algorithm that is based on the Euclidean distance. To reduce the computational burden of calculating the EMD for all volume pairs, we employ a wavelet-based approximation to the EMD which reduces the computation of the pairwise EMDs to a computation of pairwise weighted-$\ell_1$ distances between wavelet coefficient vectors.

Cryo-EM reconstruction of continuous heterogeneity by Laplacian spectral volumes

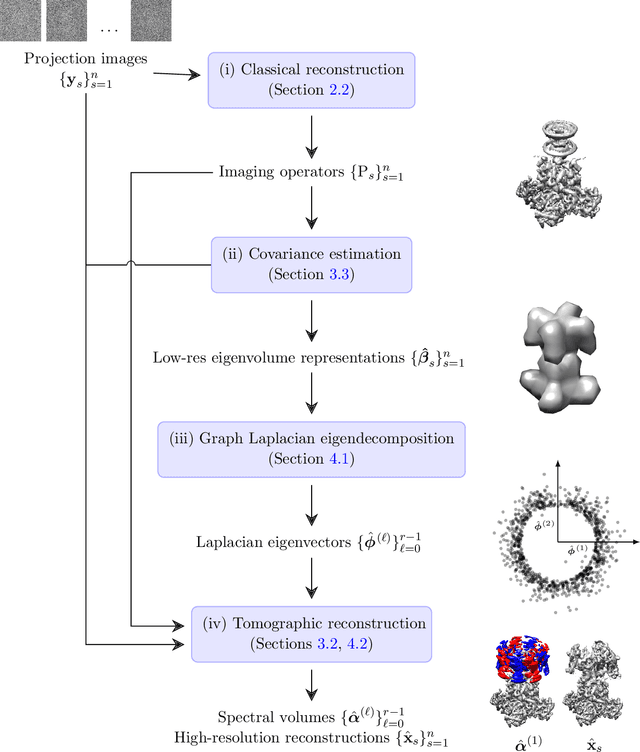
Single-particle electron cryomicroscopy is an essential tool for high-resolution 3D reconstruction of proteins and other biological macromolecules. An important challenge in cryo-EM is the reconstruction of non-rigid molecules with parts that move and deform. Traditional reconstruction methods fail in these cases, resulting in smeared reconstructions of the moving parts. This poses a major obstacle for structural biologists, who need high-resolution reconstructions of entire macromolecules, moving parts included. To address this challenge, we present a new method for the reconstruction of macromolecules exhibiting continuous heterogeneity. The proposed method uses projection images from multiple viewing directions to construct a graph Laplacian through which the manifold of three-dimensional conformations is analyzed. The 3D molecular structures are then expanded in a basis of Laplacian eigenvectors, using a novel generalized tomographic reconstruction algorithm to compute the expansion coefficients. These coefficients, which we name spectral volumes, provide a high-resolution visualization of the molecular dynamics. We provide a theoretical analysis and evaluate the method empirically on several simulated data sets.

Rescaling and other forms of unsupervised preprocessing introduce bias into cross-validation

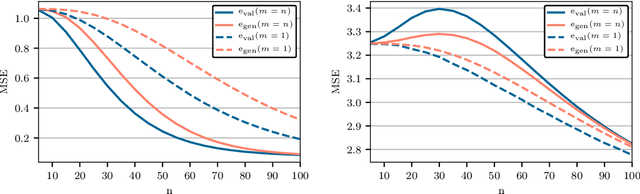
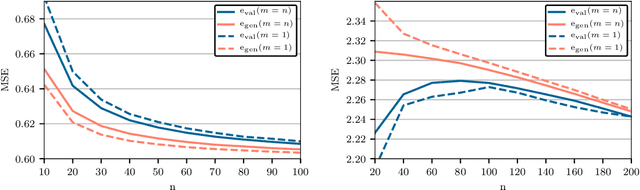
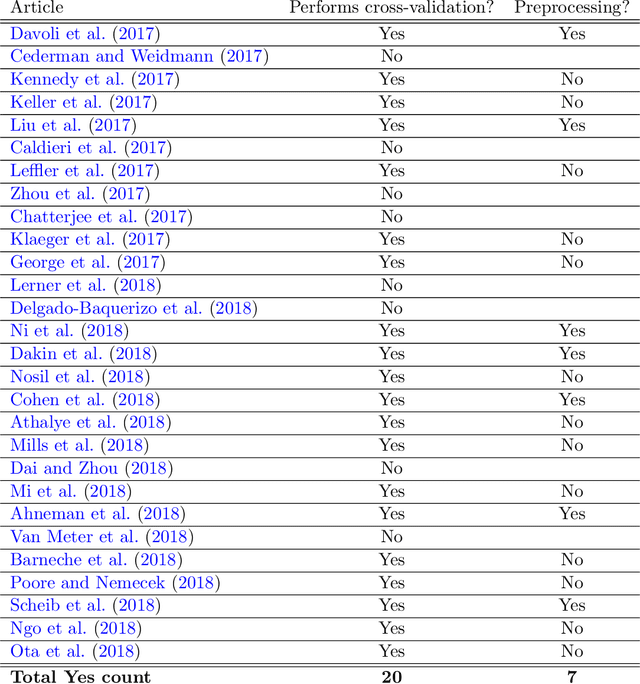
Cross-validation of predictive models is the de-facto standard for model selection and evaluation. In proper use, it provides an unbiased estimate of a model's predictive performance. However, data sets often undergo a preliminary data-dependent transformation, such as feature rescaling or dimensionality reduction, prior to cross-validation. It is widely believed that such a preprocessing stage, if done in an unsupervised manner that does not consider the class labels or response values, has no effect on the validity of cross-validation. In this paper, we show that this belief is not true. Preliminary preprocessing can introduce either a positive or negative bias into the estimates of model performance. Thus, it may lead to sub-optimal choices of model parameters and invalid inference. In light of this, the scientific community should re-examine the use of preliminary preprocessing prior to cross-validation across the various application domains. By default, all data transformations, including unsupervised preprocessing stages, should be learned only from the training samples, and then merely applied to the validation and testing samples.

Semiparametric Classification of Forest Graphical Models

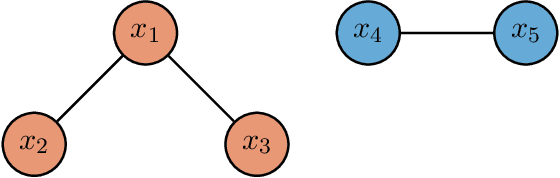
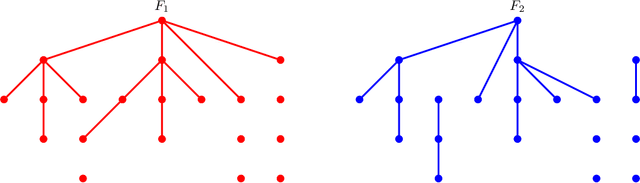
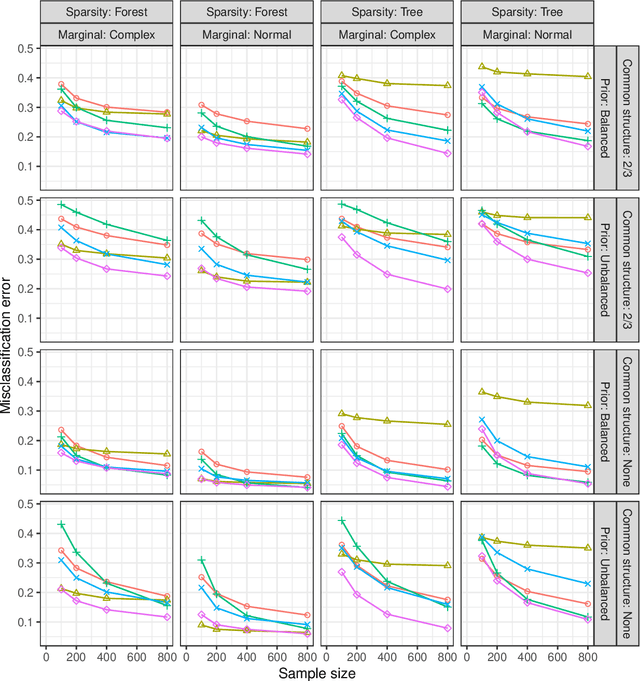
We propose a new semiparametric approach to binary classification that exploits the modeling flexibility of sparse graphical models. Specifically, we assume that each class can be represented by a forest-structured graphical model. Under this assumption, the optimal classifier is linear in the log of the one- and two-dimensional marginal densities. Our proposed procedure non-parametrically estimates the univariate and bivariate marginal densities, maps each sample to the logarithm of these estimated densities and constructs a linear SVM in the transformed space. We prove convergence of the resulting classifier to an oracle SVM classifier and give finite sample bounds on its excess risk. Experiments with simulated and real data indicate that the resulting classifier is competitive with several popular methods across a range of applications.

Minimax-optimal semi-supervised regression on unknown manifolds

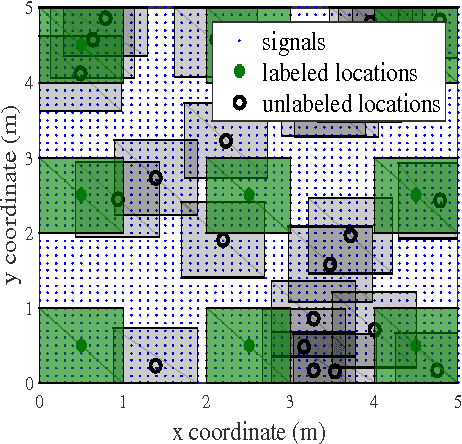
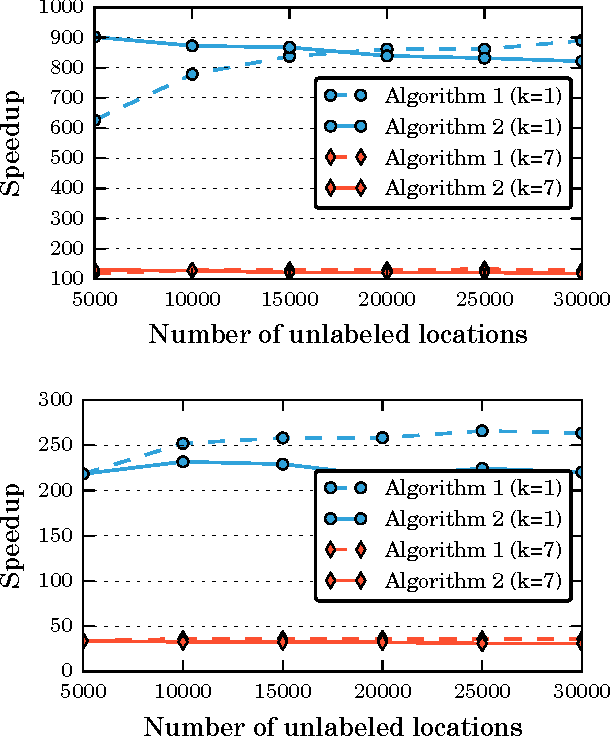
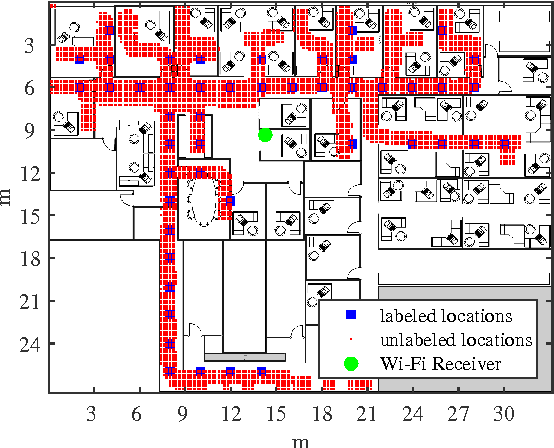
We consider semi-supervised regression when the predictor variables are drawn from an unknown manifold. A simple two step approach to this problem is to: (i) estimate the manifold geodesic distance between any pair of points using both the labeled and unlabeled instances; and (ii) apply a k nearest neighbor regressor based on these distance estimates. We prove that given sufficiently many unlabeled points, this simple method of geodesic kNN regression achieves the optimal finite-sample minimax bound on the mean squared error, as if the manifold were known. Furthermore, we show how this approach can be efficiently implemented, requiring only O(k N log N) operations to estimate the regression function at all N labeled and unlabeled points. We illustrate this approach on two datasets with a manifold structure: indoor localization using WiFi fingerprints and facial pose estimation. In both cases, geodesic kNN is more accurate and much faster than the popular Laplacian eigenvector regressor.