Mixed Semi-Supervised Generalized-Linear-Regression with applications to Deep learning

We present a methodology for using unlabeled data to design semi supervised learning (SSL) methods that improve the prediction performance of supervised learning for regression tasks. The main idea is to design different mechanisms for integrating the unlabeled data, and include in each of them a mixing parameter $\alpha$, controlling the weight given to the unlabeled data. Focusing on Generalized-Linear-Models (GLM), we analyze the characteristics of different mixing mechanisms, and prove that in all cases, it is inevitably beneficial to integrate the unlabeled data with some non-zero mixing ratio $\alpha>0$, in terms of predictive performance. Moreover, we provide a rigorous framework for estimating the best mixing ratio $\alpha^*$ where mixed-SSL delivers the best predictive performance, while using the labeled and the unlabeled data on hand. The effectiveness of our methodology in delivering substantial improvement compared to the standard supervised models, under a variety of settings, is demonstrated empirically through extensive simulation, in a manner that supports the theoretical analysis. We also demonstrate the applicability of our methodology (with some intuitive modifications) in improving more complex models such as deep neural networks, in a real-world regression tasks.

Integrating Random Effects in Deep Neural Networks

Modern approaches to supervised learning like deep neural networks (DNNs) typically implicitly assume that observed responses are statistically independent. In contrast, correlated data are prevalent in real-life large-scale applications, with typical sources of correlation including spatial, temporal and clustering structures. These correlations are either ignored by DNNs, or ad-hoc solutions are developed for specific use cases. We propose to use the mixed models framework to handle correlated data in DNNs. By treating the effects underlying the correlation structure as random effects, mixed models are able to avoid overfitted parameter estimates and ultimately yield better predictive performance. The key to combining mixed models and DNNs is using the Gaussian negative log-likelihood (NLL) as a natural loss function that is minimized with DNN machinery including stochastic gradient descent (SGD). Since NLL does not decompose like standard DNN loss functions, the use of SGD with NLL presents some theoretical and implementation challenges, which we address. Our approach which we call LMMNN is demonstrated to improve performance over natural competitors in various correlation scenarios on diverse simulated and real datasets. Our focus is on a regression setting and tabular datasets, but we also show some results for classification. Our code is available at https://github.com/gsimchoni/lmmnn.

Trees-Based Models for Correlated Data

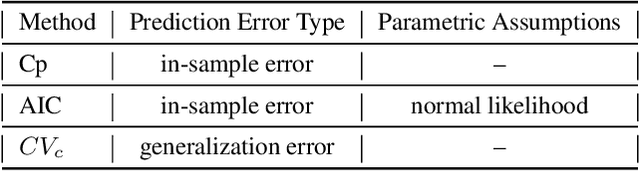
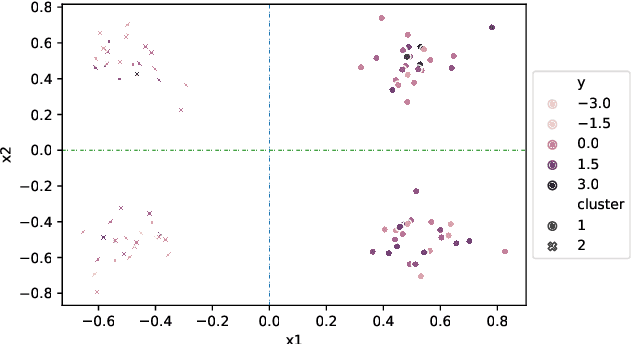
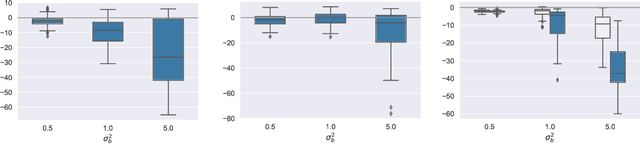
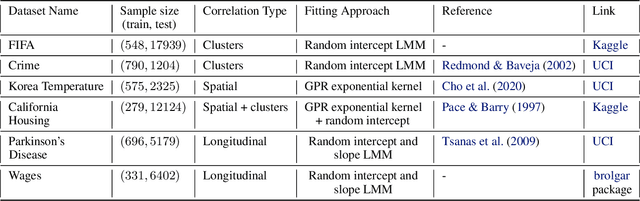
This paper presents a new approach for trees-based regression, such as simple regression tree, random forest and gradient boosting, in settings involving correlated data. We show the problems that arise when implementing standard trees-based regression models, which ignore the correlation structure. Our new approach explicitly takes the correlation structure into account in the splitting criterion, stopping rules and fitted values in the leaves, which induces some major modifications of standard methodology. The superiority of our new approach over trees-based models that do not account for the correlation is supported by simulation experiments and real data analyses.

Semi-Supervised Empirical Risk Minimization: When can unlabeled data improve prediction

We present a general methodology for using unlabeled data to design semi supervised learning (SSL) variants of the Empirical Risk Minimization (ERM) learning process. Focusing on generalized linear regression, we provide a careful treatment of the effectiveness of the SSL to improve prediction performance. The key ideas are carefully considering the null model as a competitor, and utilizing the unlabeled data to determine signal-noise combinations where the SSL outperforms both the ERM learning and the null model. In the special case of linear regression with Gaussian covariates, we show that the previously suggested semi-supervised estimator is in fact not capable of improving on both the supervised estimator and the null model simultaneously. However, the new estimator presented in this work, can achieve an improvement of $O(1/n)$ term over both competitors simultaneously. On the other hand, we show that in other scenarios, such as non-Gaussian covariates, misspecified linear regression, or generalized linear regression with non-linear link functions, having unlabeled data can derive substantial improvement in prediction by applying our suggested SSL approach. Moreover, it is possible to identify the usefulness of the SSL, by using the dedicated formulas we establish throughout this work. This is shown empirically through extensive simulations.

Surprises in High-Dimensional Ridgeless Least Squares Interpolation

Interpolators---estimators that achieve zero training error---have attracted growing attention in machine learning, mainly because state-of-the art neural networks appear to be models of this type. In this paper, we study minimum $\ell_2$ norm (`ridgeless') interpolation in high-dimensional least squares regression. We consider two different models for the feature distribution: a linear model, where the feature vectors $x_i \in {\mathbb R}^p$ are obtained by applying a linear transform to a vector of i.i.d.\ entries, $x_i = \Sigma^{1/2} z_i$ (with $z_i \in {\mathbb R}^p$); and a nonlinear model, where the feature vectors are obtained by passing the input through a random one-layer neural network, $x_i = \varphi(W z_i)$ (with $z_i \in {\mathbb R}^d$, $W \in {\mathbb R}^{p \times d}$ a matrix of i.i.d.\ entries, and $\varphi$ an activation function acting componentwise on $W z_i$). We recover---in a precise quantitative way---several phenomena that have been observed in large-scale neural networks and kernel machines, including the `double descent' behavior of the prediction risk, and the potential benefits of overparametrization.

Rescaling and other forms of unsupervised preprocessing introduce bias into cross-validation

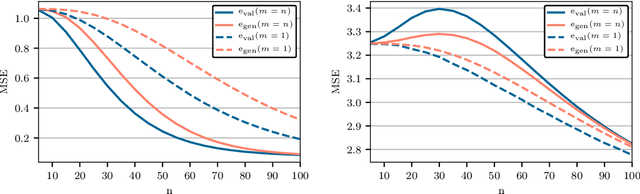
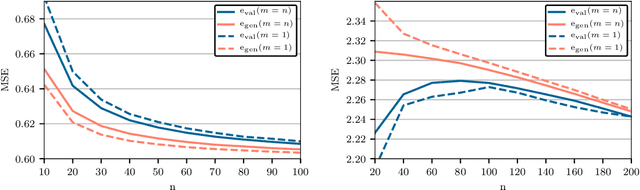
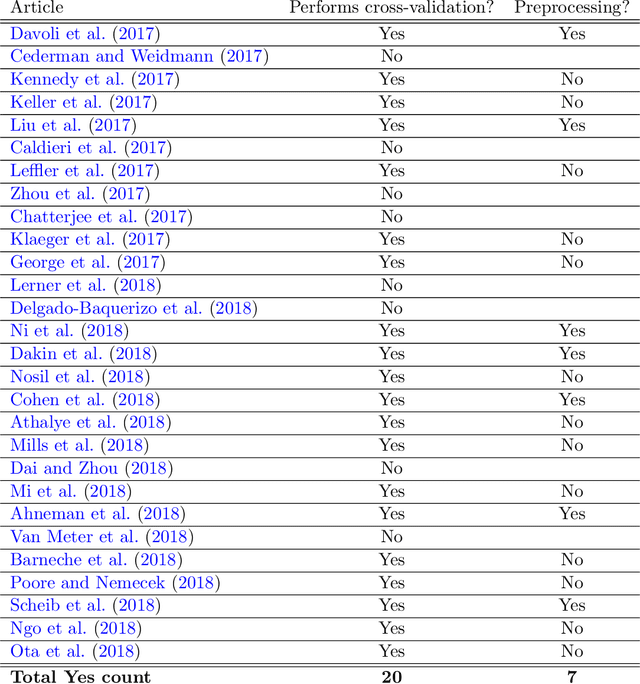
Cross-validation of predictive models is the de-facto standard for model selection and evaluation. In proper use, it provides an unbiased estimate of a model's predictive performance. However, data sets often undergo a preliminary data-dependent transformation, such as feature rescaling or dimensionality reduction, prior to cross-validation. It is widely believed that such a preprocessing stage, if done in an unsupervised manner that does not consider the class labels or response values, has no effect on the validity of cross-validation. In this paper, we show that this belief is not true. Preliminary preprocessing can introduce either a positive or negative bias into the estimates of model performance. Thus, it may lead to sub-optimal choices of model parameters and invalid inference. In light of this, the scientific community should re-examine the use of preliminary preprocessing prior to cross-validation across the various application domains. By default, all data transformations, including unsupervised preprocessing stages, should be learned only from the training samples, and then merely applied to the validation and testing samples.

Capturing Between-Tasks Covariance and Similarities Using Multivariate Linear Mixed Models

We consider the problem of predicting several response variables using the same set of explanatory variables. This setting naturally induces a group structure over the coefficient matrix, in which every explanatory variable corresponds to a set of related coefficients. Most of the existing methods that utilize this group formation assume that the similarities between related coefficients arise solely through a joint sparsity structure. In this paper, we propose a procedure for constructing an estimator of a multivariate regression coefficient matrix that directly models and captures the within-group similarities, by employing a multivariate linear mixed model formulation, with joint estimation of covariance matrices for coefficients and errors via penalized likelihood. Our approach, which we term Multivariate random Regression with Covariance Estimation (MrRCE) encourages structured similarity in parameters, in which coefficients for the same variable in related tasks sharing the same sign and similar magnitude. We illustrate the benefits of our approach in synthetic and real examples, and show that the proposed method outperforms natural competitors and alternative estimators under several model settings.

Lossless (and Lossy) Compression of Random Forests

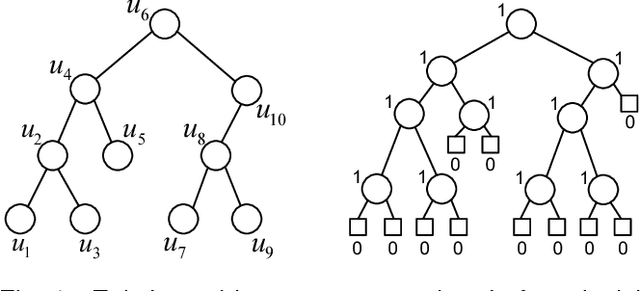
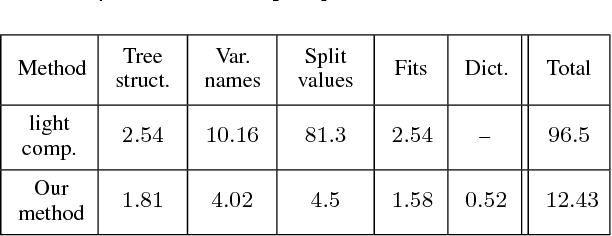
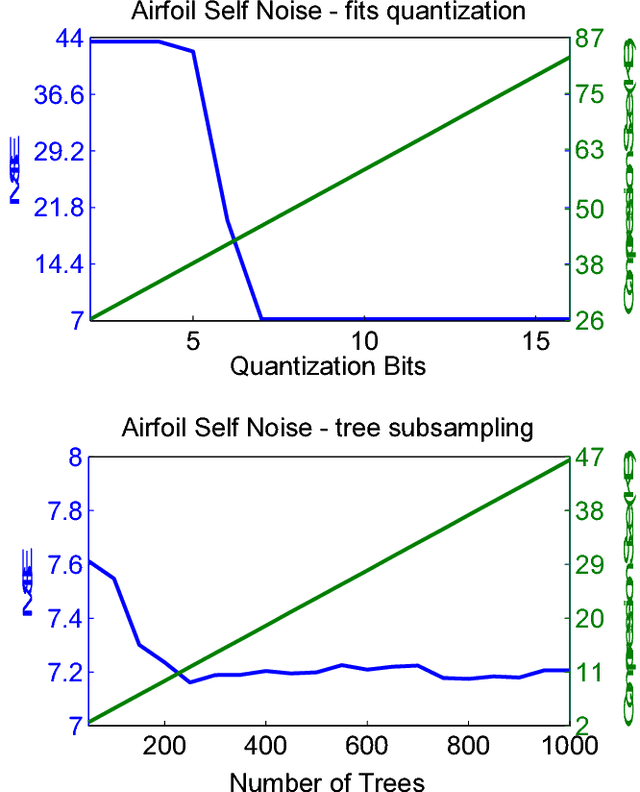
Ensemble methods are among the state-of-the-art predictive modeling approaches. Applied to modern big data, these methods often require a large number of sub-learners, where the complexity of each learner typically grows with the size of the dataset. This phenomenon results in an increasing demand for storage space, which may be very costly. This problem mostly manifests in a subscriber based environment, where a user-specific ensemble needs to be stored on a personal device with strict storage limitations (such as a cellular device). In this work we introduce a novel method for lossless compression of tree-based ensemble methods, focusing on random forests. Our suggested method is based on probabilistic modeling of the ensemble's trees, followed by model clustering via Bregman divergence. This allows us to find a minimal set of models that provides an accurate description of the trees, and at the same time is small enough to store and maintain. Our compression scheme demonstrates high compression rates on a variety of modern datasets. Importantly, our scheme enables predictions from the compressed format and a perfect reconstruction of the original ensemble. In addition, we introduce a theoretically sound lossy compression scheme, which allows us to control the trade-off between the distortion and the coding rate.

Linear Independent Component Analysis over Finite Fields: Algorithms and Bounds

Independent Component Analysis (ICA) is a statistical tool that decomposes an observed random vector into components that are as statistically independent as possible. ICA over finite fields is a special case of ICA, in which both the observations and the decomposed components take values over a finite alphabet. This problem is also known as minimal redundancy representation or factorial coding. In this work we focus on linear methods for ICA over finite fields. We introduce a basic lower bound which provides a fundamental limit to the ability of any linear solution to solve this problem. Based on this bound, we present a greedy algorithm that outperforms all currently known methods. Importantly, we show that the overhead of our suggested algorithm (compared with the lower bound) typically decreases, as the scale of the problem grows. In addition, we provide a sub-optimal variant of our suggested method that significantly reduces the computational complexity at a relatively small cost in performance. Finally, we discuss the universal abilities of linear transformations in decomposing random vectors, compared with existing non-linear solutions.

The Everlasting Database: Statistical Validity at a Fair Price

The problem of handling adaptivity in data analysis, intentional or not, permeates a variety of fields, including test-set overfitting in ML challenges and the accumulation of invalid scientific discoveries. We propose a mechanism for answering an arbitrarily long sequence of potentially adaptive statistical queries, by charging a price for each query and using the proceeds to collect additional samples. Crucially, we guarantee statistical validity without any assumptions on how the queries are generated. We also ensure with high probability that the cost for $M$ non-adaptive queries is $O(\log M)$, while the cost to a potentially adaptive user who makes $M$ queries that do not depend on any others is $O(\sqrt{M})$.