Distribution Estimation under the Infinity Norm

We present novel bounds for estimating discrete probability distributions under the $\ell_\infty$ norm. These are nearly optimal in various precise senses, including a kind of instance-optimality. Our data-dependent convergence guarantees for the maximum likelihood estimator significantly improve upon the currently known results. A variety of techniques are utilized and innovated upon, including Chernoff-type inequalities and empirical Bernstein bounds. We illustrate our results in synthetic and real-world experiments. Finally, we apply our proposed framework to a basic selective inference problem, where we estimate the most frequent probabilities in a sample.

Optimal detection of non-overlapping images via combinatorial auction

This paper studies the classical problem of detecting the location of multiple image occurrences in a two-dimensional, noisy measurement. Assuming the image occurrences do not overlap, we formulate this task as a constrained maximum likelihood optimization problem. We show that the maximum likelihood estimator is equivalent to an instance of the winner determination problem from the field of combinatorial auction, and that the solution can be obtained by searching over a binary tree. We then design a pruning mechanism that significantly accelerates the runtime of the search. We demonstrate on simulations and electron microscopy data sets that the proposed algorithm provides accurate detection in challenging regimes of high noise levels and densely packed image occurrences.

Confidence Intervals for Unobserved Events

Consider a finite sample from an unknown distribution over a countable alphabet. Unobserved events are alphabet symbols which do not appear in the sample. Estimating the probabilities of unobserved events is a basic problem in statistics and related fields, which was extensively studied in the context of point estimation. In this work we introduce a novel interval estimation scheme for unobserved events. Our proposed framework applies selective inference, as we construct confidence intervals (CIs) for the desired set of parameters. Interestingly, we show that obtained CIs are dimension-free, as they do not grow with the alphabet size. Further, we show that these CIs are (almost) tight, in the sense that they cannot be further improved without violating the prescribed coverage rate. We demonstrate the performance of our proposed scheme in synthetic and real-world experiments, showing a significant improvement over the alternatives. Finally, we apply our proposed scheme to large alphabet modeling. We introduce a novel simultaneous CI scheme for large alphabet distributions which outperforms currently known methods while maintaining the prescribed coverage rate.

K-sample Multiple Hypothesis Testing for Signal Detection

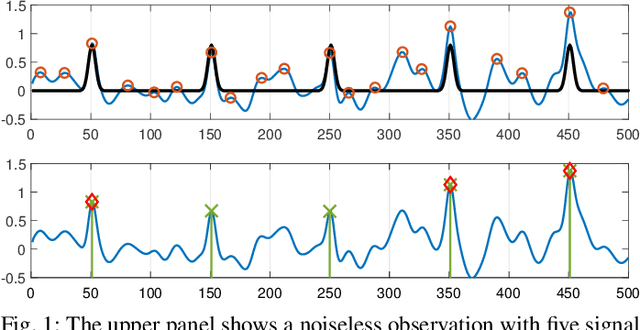
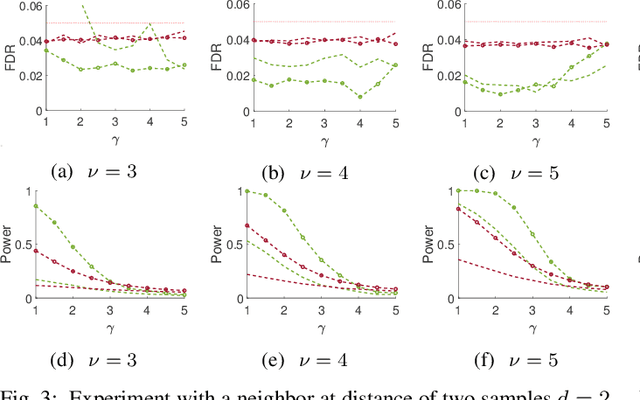
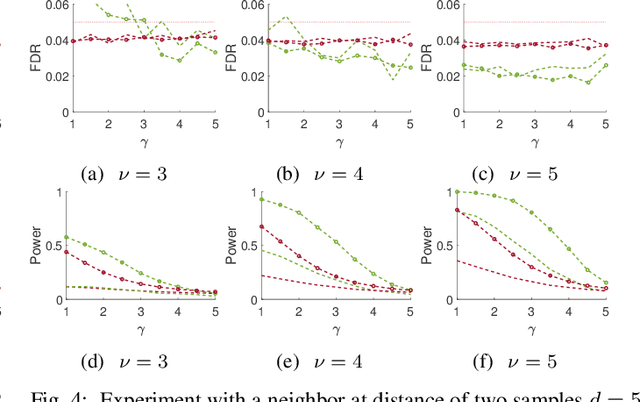
This paper studies the classical problem of estimating the locations of signal occurrences in a noisy measurement. Based on a multiple hypothesis testing scheme, we design a K-sample statistical test to control the false discovery rate (FDR). Specifically, we first convolve the noisy measurement with a smoothing kernel, and find all local maxima. Then, we evaluate the joint probability of K entries in the vicinity of each local maximum, derive the corresponding p-value, and apply the Benjamini-Hochberg procedure to account for multiplicity. We demonstrate through extensive experiments that our proposed method, with K=2, controls the prescribed FDR while increasing the power compared to a one-sample test.

Signal detection with dynamic programming

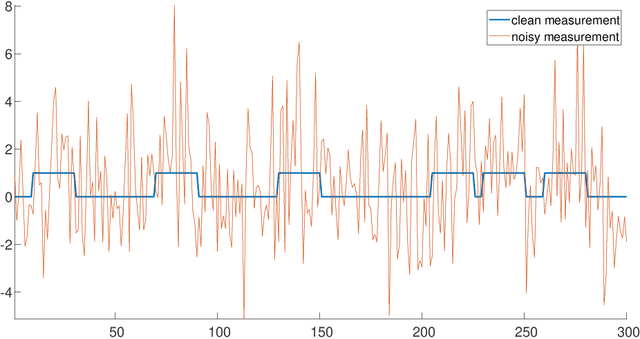
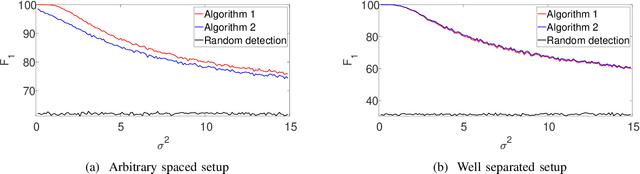
This paper studies the classical problem of detecting the locations of signal occurrences in a one-dimensional noisy measurement. Assuming the signal occurrences do not overlap, we formulate the detection task as a constrained likelihood optimization problem, and design a computationally efficient dynamic program that attains its optimal solution. Our proposed framework is scalable, simple to implement, and robust to model uncertainties. We show by extensive numerical experiments that our algorithm accurately estimates the locations in dense and noisy environments, and outperforms alternative methods.

Feature Importance in Gradient Boosting Trees with Cross-Validation Feature Selection

Gradient Boosting Machines (GBM) are among the go-to algorithms on tabular data, which produce state of the art results in many prediction tasks. Despite its popularity, the GBM framework suffers from a fundamental flaw in its base learners. Specifically, most implementations utilize decision trees that are typically biased towards categorical variables with large cardinalities. The effect of this bias was extensively studied over the years, mostly in terms of predictive performance. In this work, we extend the scope and study the effect of biased base learners on GBM feature importance (FI) measures. We show that although these implementation demonstrate highly competitive predictive performance, they still, surprisingly, suffer from bias in FI. By utilizing cross-validated (CV) unbiased base learners, we fix this flaw at a relatively low computational cost. We demonstrate the suggested framework in a variety of synthetic and real-world setups, showing a significant improvement in all GBM FI measures while maintaining relatively the same level of prediction accuracy.

Neural Joint Entropy Estimation

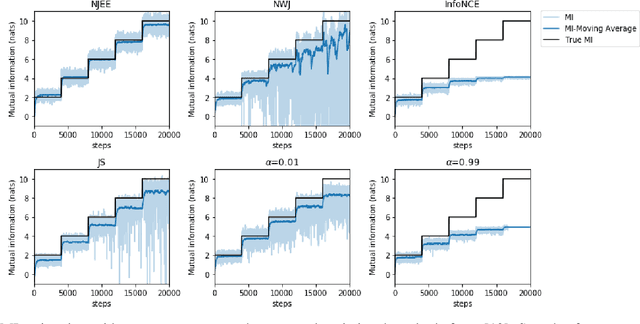
Estimating the entropy of a discrete random variable is a fundamental problem in information theory and related fields. This problem has many applications in various domains, including machine learning, statistics and data compression. Over the years, a variety of estimation schemes have been suggested. However, despite significant progress, most methods still struggle when the sample is small, compared to the variable's alphabet size. In this work, we introduce a practical solution to this problem, which extends the work of McAllester and Statos (2020). The proposed scheme uses the generalization abilities of cross-entropy estimation in deep neural networks (DNNs) to introduce improved entropy estimation accuracy. Furthermore, we introduce a family of estimators for related information-theoretic measures, such as conditional entropy and mutual information. We show that these estimators are strongly consistent and demonstrate their performance in a variety of use-cases. First, we consider large alphabet entropy estimation. Then, we extend the scope to mutual information estimation. Next, we apply the proposed scheme to conditional mutual information estimation, as we focus on independence testing tasks. Finally, we study a transfer entropy estimation problem. The proposed estimators demonstrate improved performance compared to existing methods in all tested setups.

An Information-Theoretic Framework for Non-linear Canonical Correlation Analysis

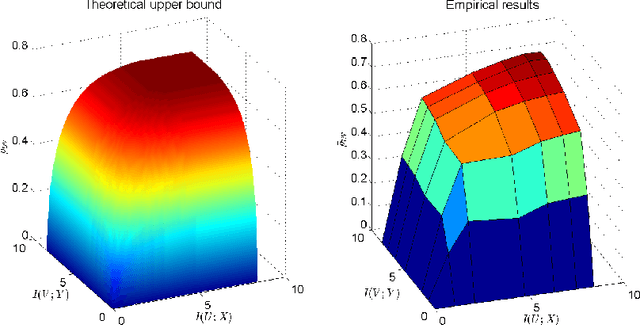
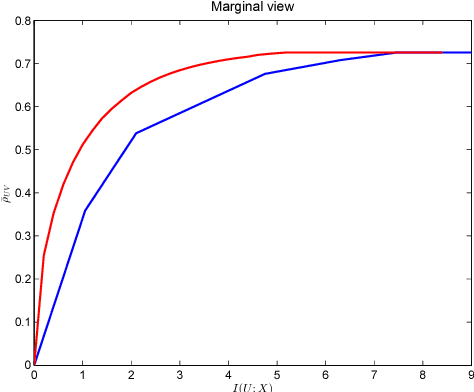
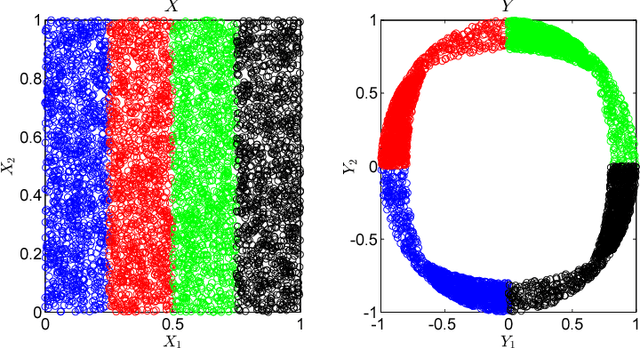
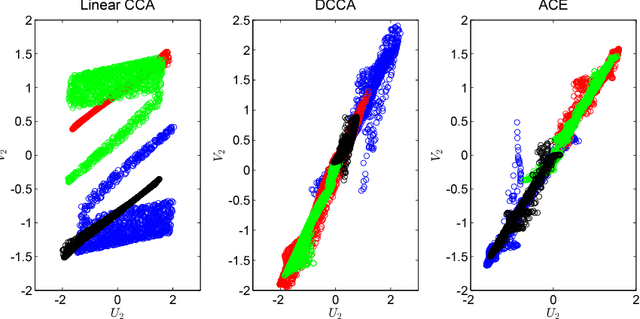
Canonical Correlation Analysis (CCA) is a linear representation learning method that seeks maximally correlated variables in multi-view data. Non-linear CCA extends this notion to a broader family of transformations, which are more powerful for many real-world applications. Given the joint probability, the Alternating Conditional Expectation (ACE) provides an optimal solution to the non-linear CCA problem. However, it suffers from limited performance and an increasing computational burden when only a finite number of observations is available. In this work we introduce an information-theoretic framework for the non-linear CCA problem (ITCCA), which extends the classical ACE approach. Our suggested framework seeks compressed representations of the data that allow a maximal level of correlation. This way we control the trade-off between the flexibility and the complexity of the representation. Our approach demonstrates favorable performance at a reduced computational burden, compared to non-linear alternatives, in a finite sample size regime. Further, ITCCA provides theoretical bounds and optimality conditions, as we establish fundamental connections to rate-distortion theory, the information bottleneck and remote source coding. In addition, it implies a "soft" dimensionality reduction, as the compression level is measured (and governed) by the mutual information between the original noisy data and the signals that we extract.

Lossless (and Lossy) Compression of Random Forests

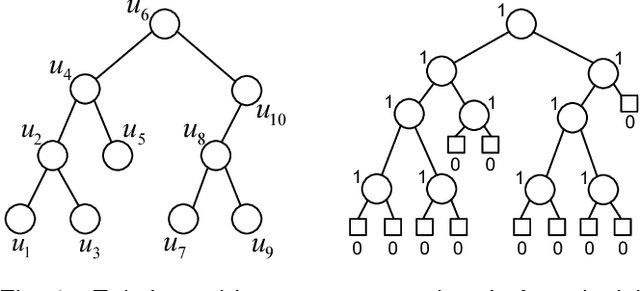
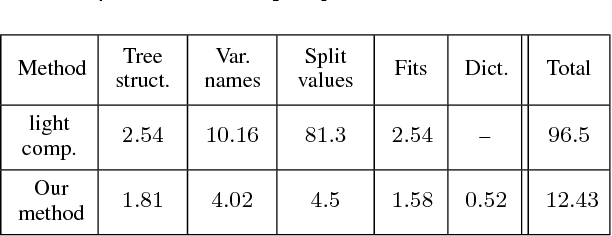
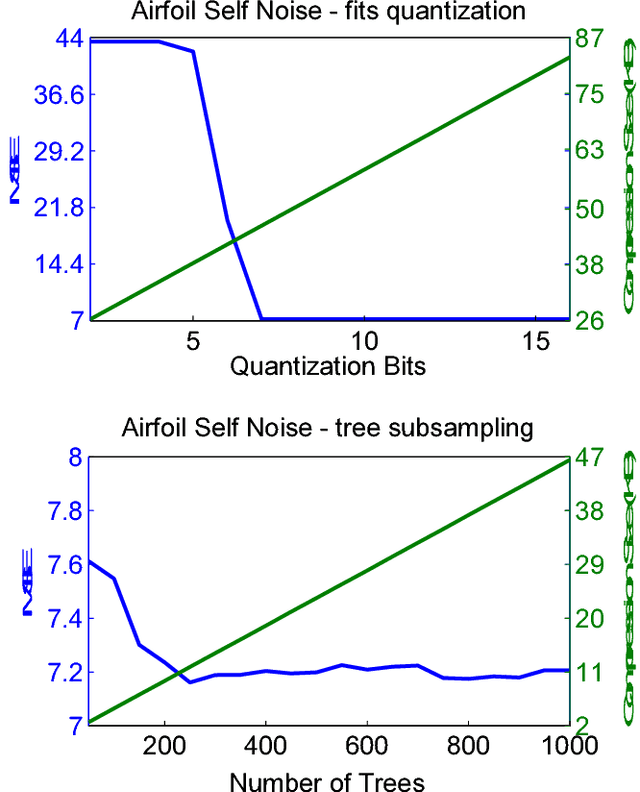
Ensemble methods are among the state-of-the-art predictive modeling approaches. Applied to modern big data, these methods often require a large number of sub-learners, where the complexity of each learner typically grows with the size of the dataset. This phenomenon results in an increasing demand for storage space, which may be very costly. This problem mostly manifests in a subscriber based environment, where a user-specific ensemble needs to be stored on a personal device with strict storage limitations (such as a cellular device). In this work we introduce a novel method for lossless compression of tree-based ensemble methods, focusing on random forests. Our suggested method is based on probabilistic modeling of the ensemble's trees, followed by model clustering via Bregman divergence. This allows us to find a minimal set of models that provides an accurate description of the trees, and at the same time is small enough to store and maintain. Our compression scheme demonstrates high compression rates on a variety of modern datasets. Importantly, our scheme enables predictions from the compressed format and a perfect reconstruction of the original ensemble. In addition, we introduce a theoretically sound lossy compression scheme, which allows us to control the trade-off between the distortion and the coding rate.

MSc Dissertation: Exclusive Row Biclustering for Gene Expression Using a Combinatorial Auction Approach

The availability of large microarray data has led to a growing interest in biclustering methods in the past decade. Several algorithms have been proposed to identify subsets of genes and conditions according to different similarity measures and under varying constraints. In this paper we focus on the exclusive row biclustering problem for gene expression data sets, in which each row can only be a member of a single bicluster while columns can participate in multiple ones. This type of biclustering may be adequate, for example, for clustering groups of cancer patients where each patient (row) is expected to be carrying only a single type of cancer, while each cancer type is associated with multiple (and possibly overlapping) genes (columns). We present a novel method to identify these exclusive row biclusters through a combination of existing biclustering algorithms and combinatorial auction techniques. We devise an approach for tuning the threshold for our algorithm based on comparison to a null model in the spirit of the Gap statistic approach. We demonstrate our approach on both synthetic and real-world gene expression data and show its power in identifying large span non-overlapping rows sub matrices, while considering their unique nature. The Gap statistic approach succeeds in identifying appropriate thresholds in all our examples.