Distributional reasoning in LLMs: Parallel reasoning processes in multi-hop reasoning

Large language models (LLMs) have shown an impressive ability to perform tasks believed to require thought processes. When the model does not document an explicit thought process, it becomes difficult to understand the processes occurring within its hidden layers and to determine if these processes can be referred to as reasoning. We introduce a novel and interpretable analysis of internal multi-hop reasoning processes in LLMs. We demonstrate that the prediction process for compositional reasoning questions can be modeled using a simple linear transformation between two semantic category spaces. We show that during inference, the middle layers of the network generate highly interpretable embeddings that represent a set of potential intermediate answers for the multi-hop question. We use statistical analyses to show that a corresponding subset of tokens is activated in the model's output, implying the existence of parallel reasoning paths. These observations hold true even when the model lacks the necessary knowledge to solve the task. Our findings can help uncover the strategies that LLMs use to solve reasoning tasks, offering insights into the types of thought processes that can emerge from artificial intelligence. Finally, we also discuss the implication of cognitive modeling of these results.

Neural Joint Entropy Estimation

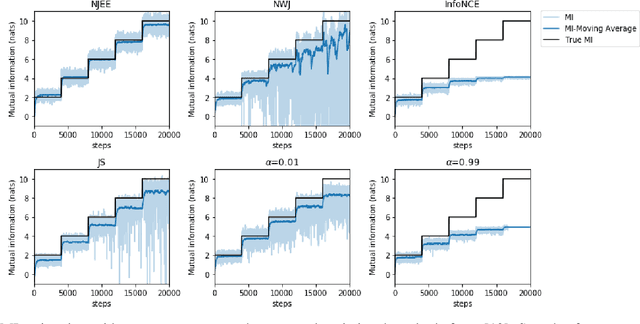
Estimating the entropy of a discrete random variable is a fundamental problem in information theory and related fields. This problem has many applications in various domains, including machine learning, statistics and data compression. Over the years, a variety of estimation schemes have been suggested. However, despite significant progress, most methods still struggle when the sample is small, compared to the variable's alphabet size. In this work, we introduce a practical solution to this problem, which extends the work of McAllester and Statos (2020). The proposed scheme uses the generalization abilities of cross-entropy estimation in deep neural networks (DNNs) to introduce improved entropy estimation accuracy. Furthermore, we introduce a family of estimators for related information-theoretic measures, such as conditional entropy and mutual information. We show that these estimators are strongly consistent and demonstrate their performance in a variety of use-cases. First, we consider large alphabet entropy estimation. Then, we extend the scope to mutual information estimation. Next, we apply the proposed scheme to conditional mutual information estimation, as we focus on independence testing tasks. Finally, we study a transfer entropy estimation problem. The proposed estimators demonstrate improved performance compared to existing methods in all tested setups.