Learner Attentiveness and Engagement Analysis in Online Education Using Computer Vision

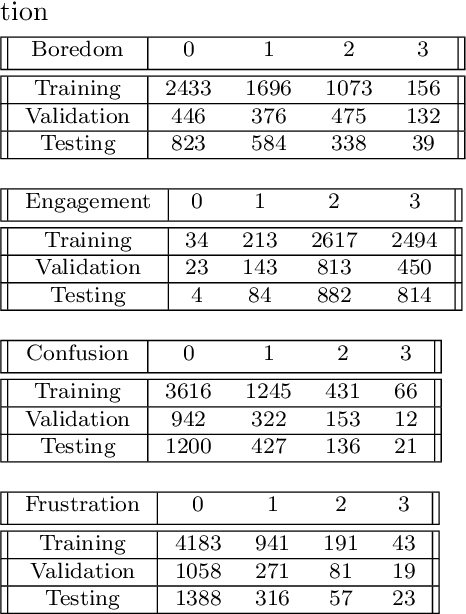
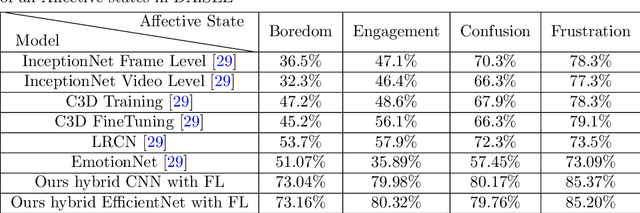
In recent times, online education and the usage of video-conferencing platforms have experienced massive growth. Due to the limited scope of a virtual classroom, it may become difficult for instructors to analyze learners' attention and comprehension in real time while teaching. In the digital mode of education, it would be beneficial for instructors to have an automated feedback mechanism to be informed regarding learners' attentiveness at any given time. This research presents a novel computer vision-based approach to analyze and quantify learners' attentiveness, engagement, and other affective states within online learning scenarios. This work presents the development of a multiclass multioutput classification method using convolutional neural networks on a publicly available dataset - DAiSEE. A machine learning-based algorithm is developed on top of the classification model that outputs a comprehensive attentiveness index of the learners. Furthermore, an end-to-end pipeline is proposed through which learners' live video feed is processed, providing detailed attentiveness analytics of the learners to the instructors. By comparing the experimental outcomes of the proposed method against those of previous methods, it is demonstrated that the proposed method exhibits better attentiveness detection than state-of-the-art methods. The proposed system is a comprehensive, practical, and real-time solution that is deployable and easy to use. The experimental results also demonstrate the system's efficiency in gauging learners' attentiveness.

A Non-Parametric Subspace Analysis Approach with Application to Anomaly Detection Ensembles

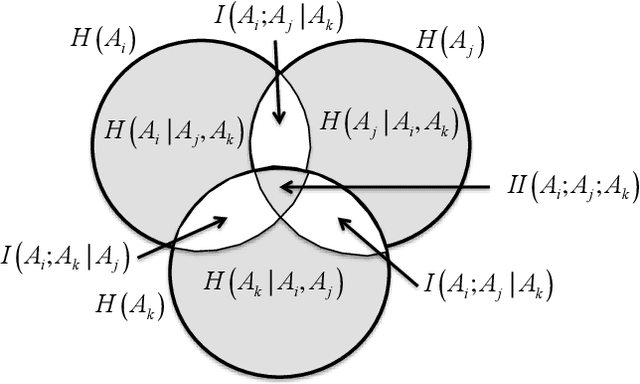
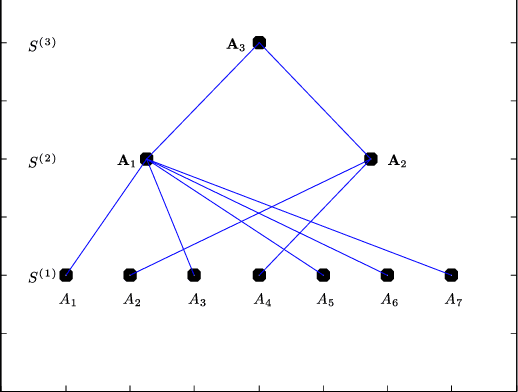
Identifying anomalies in multi-dimensional datasets is an important task in many real-world applications. A special case arises when anomalies are occluded in a small set of attributes, typically referred to as a subspace, and not necessarily over the entire data space. In this paper, we propose a new subspace analysis approach named Agglomerative Attribute Grouping (AAG) that aims to address this challenge by searching for subspaces that are comprised of highly correlative attributes. Such correlations among attributes represent a systematic interaction among the attributes that can better reflect the behavior of normal observations and hence can be used to improve the identification of two particularly interesting types of abnormal data samples: anomalies that are occluded in relatively small subsets of the attributes and anomalies that represent a new data class. AAG relies on a novel multi-attribute measure, which is derived from information theory measures of partitions, for evaluating the "information distance" between groups of data attributes. To determine the set of subspaces to use, AAG applies a variation of the well-known agglomerative clustering algorithm with the proposed multi-attribute measure as the underlying distance function. Finally, the set of subspaces is used in an ensemble for anomaly detection. Extensive evaluation demonstrates that, in the vast majority of cases, the proposed AAG method (i) outperforms classical and state-of-the-art subspace analysis methods when used in anomaly detection ensembles, and (ii) generates fewer subspaces with a fewer number of attributes each (on average), thus resulting in a faster training time for the anomaly detection ensemble. Furthermore, in contrast to existing methods, the proposed AAG method does not require any tuning of parameters.

Neural Joint Entropy Estimation

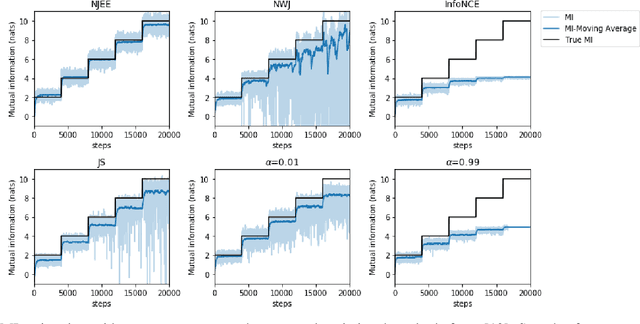
Estimating the entropy of a discrete random variable is a fundamental problem in information theory and related fields. This problem has many applications in various domains, including machine learning, statistics and data compression. Over the years, a variety of estimation schemes have been suggested. However, despite significant progress, most methods still struggle when the sample is small, compared to the variable's alphabet size. In this work, we introduce a practical solution to this problem, which extends the work of McAllester and Statos (2020). The proposed scheme uses the generalization abilities of cross-entropy estimation in deep neural networks (DNNs) to introduce improved entropy estimation accuracy. Furthermore, we introduce a family of estimators for related information-theoretic measures, such as conditional entropy and mutual information. We show that these estimators are strongly consistent and demonstrate their performance in a variety of use-cases. First, we consider large alphabet entropy estimation. Then, we extend the scope to mutual information estimation. Next, we apply the proposed scheme to conditional mutual information estimation, as we focus on independence testing tasks. Finally, we study a transfer entropy estimation problem. The proposed estimators demonstrate improved performance compared to existing methods in all tested setups.