K-sample Multiple Hypothesis Testing for Signal Detection
Paper and Code
Sep 23, 2022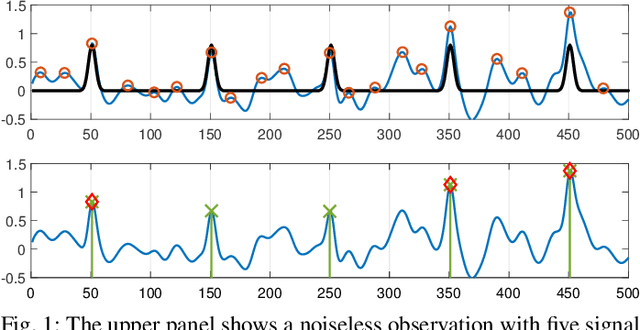

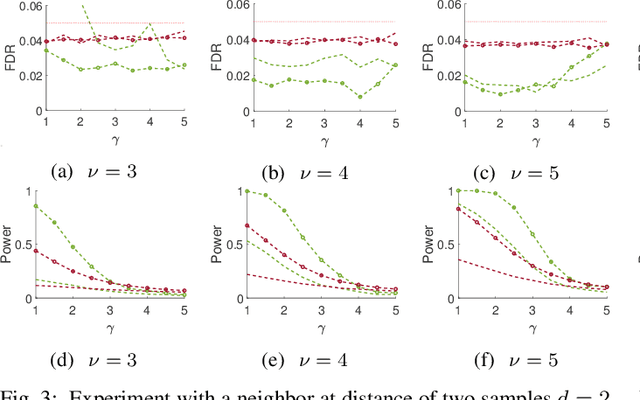
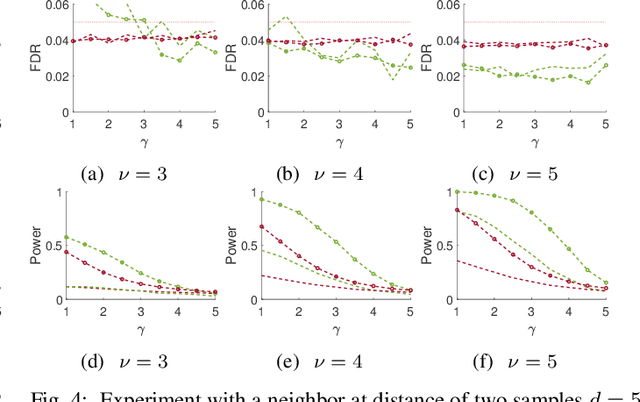
This paper studies the classical problem of estimating the locations of signal occurrences in a noisy measurement. Based on a multiple hypothesis testing scheme, we design a K-sample statistical test to control the false discovery rate (FDR). Specifically, we first convolve the noisy measurement with a smoothing kernel, and find all local maxima. Then, we evaluate the joint probability of K entries in the vicinity of each local maximum, derive the corresponding p-value, and apply the Benjamini-Hochberg procedure to account for multiplicity. We demonstrate through extensive experiments that our proposed method, with K=2, controls the prescribed FDR while increasing the power compared to a one-sample test.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge