Intrinsic Motivation in Dynamical Control Systems

Biological systems often choose actions without an explicit reward signal, a phenomenon known as intrinsic motivation. The computational principles underlying this behavior remain poorly understood. In this study, we investigate an information-theoretic approach to intrinsic motivation, based on maximizing an agent's empowerment (the mutual information between its past actions and future states). We show that this approach generalizes previous attempts to formalize intrinsic motivation, and we provide a computationally efficient algorithm for computing the necessary quantities. We test our approach on several benchmark control problems, and we explain its success in guiding intrinsically motivated behaviors by relating our information-theoretic control function to fundamental properties of the dynamical system representing the combined agent-environment system. This opens the door for designing practical artificial, intrinsically motivated controllers and for linking animal behaviors to their dynamical properties.

Detecting chaos in lineage-trees: A deep learning approach

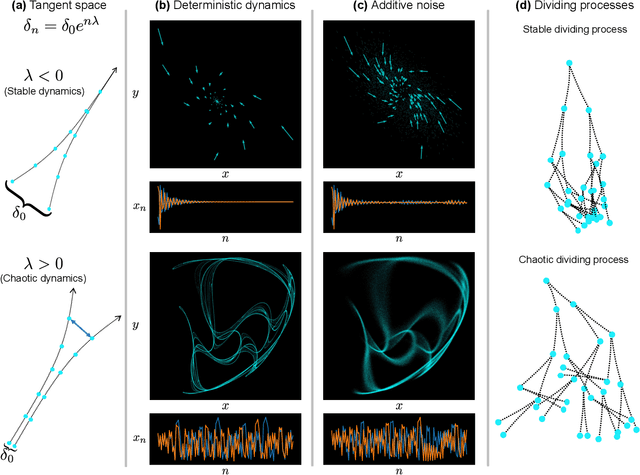
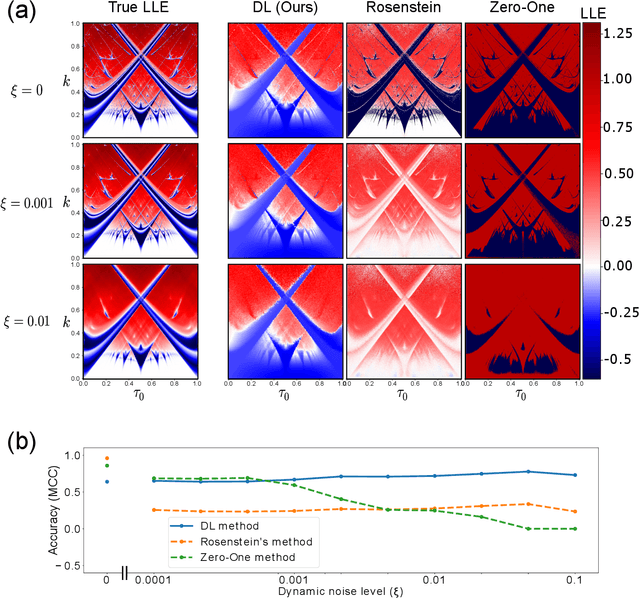
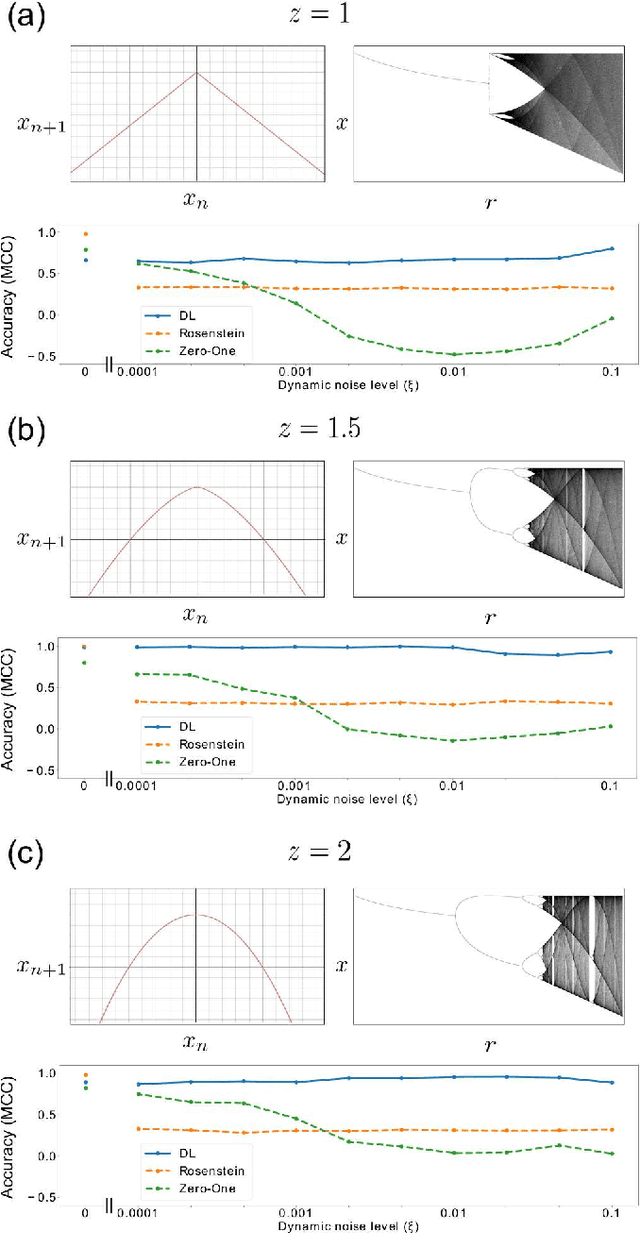
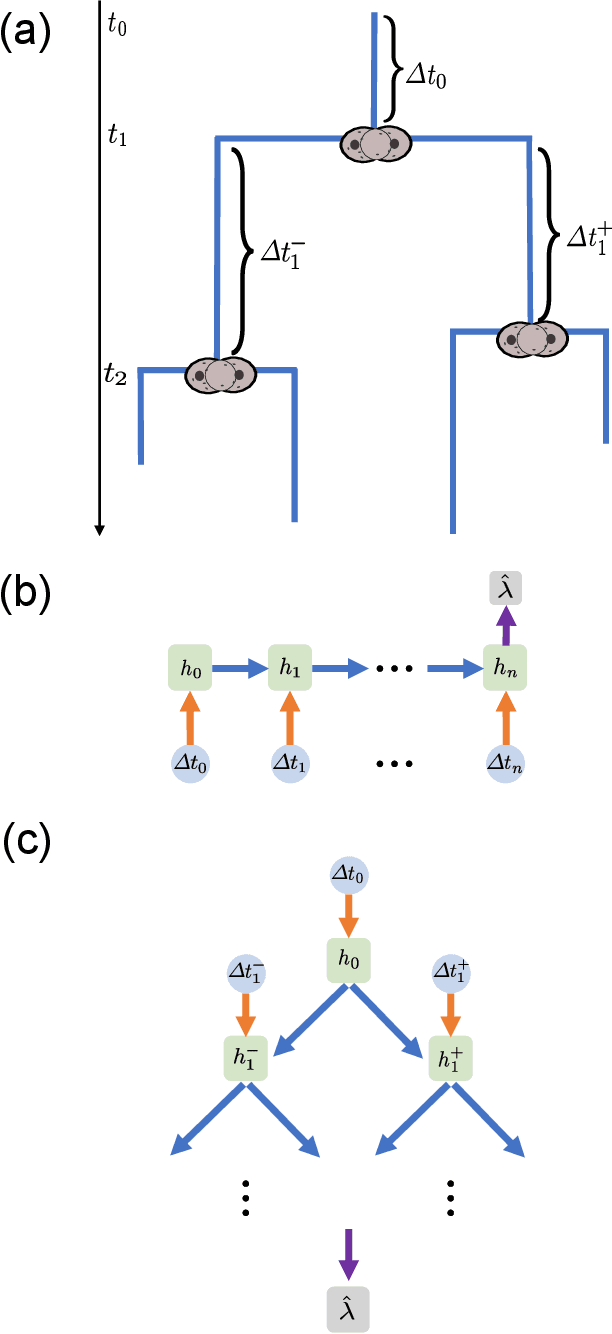
Many complex phenomena, from weather systems to heartbeat rhythm patterns, are effectively modeled as low-dimensional dynamical systems. Such systems may behave chaotically under certain conditions, and so the ability to detect chaos based on empirical measurement is an important step in characterizing and predicting these processes. Classifying a system as chaotic usually requires estimating its largest Lyapunov exponent, which quantifies the average rate of convergence or divergence of initially close trajectories in state space, and for which a positive value is generally accepted as an operational definition of chaos. Estimating the largest Lyapunov exponent from observations of a process is especially challenging in systems affected by dynamical noise, which is the case for many models of real-world processes, in particular models of biological systems. We describe a novel method for estimating the largest Lyapunov exponent from data, based on training Deep Learning models on synthetically generated trajectories, and demonstrate that this method yields accurate and noise-robust predictions given relatively short inputs and across a range of different dynamical systems. Our method is unique in that it can analyze tree-shaped data, a ubiquitous topology in biological settings, and specifically in dynamics over lineages of cells or organisms. We also characterize the types of input information extracted by our models for their predictions, allowing for a deeper understanding into the different ways by which chaos can be analyzed in different topologies.

The Dual Information Bottleneck

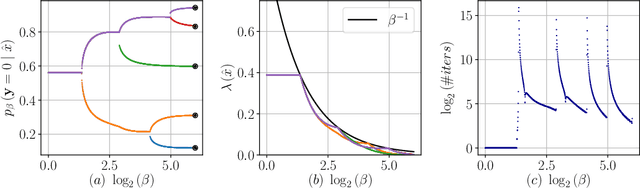
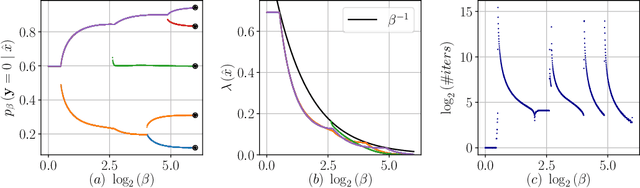
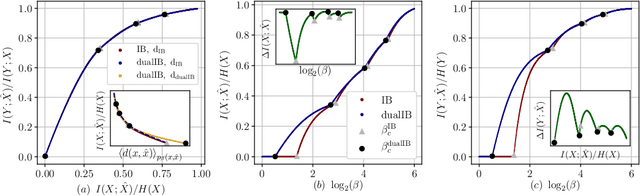
The Information Bottleneck (IB) framework is a general characterization of optimal representations obtained using a principled approach for balancing accuracy and complexity. Here we present a new framework, the Dual Information Bottleneck (dualIB), which resolves some of the known drawbacks of the IB. We provide a theoretical analysis of the dualIB framework; (i) solving for the structure of its solutions (ii) unraveling its superiority in optimizing the mean prediction error exponent and (iii) demonstrating its ability to preserve exponential forms of the original distribution. To approach large scale problems, we present a novel variational formulation of the dualIB for Deep Neural Networks. In experiments on several data-sets, we compare it to a variational form of the IB. This exposes superior Information Plane properties of the dualIB and its potential in improvement of the error.

Semantic categories of artifacts and animals reflect efficient coding

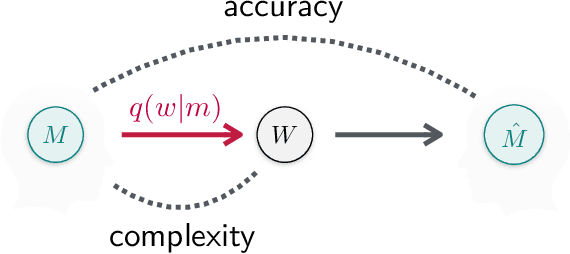
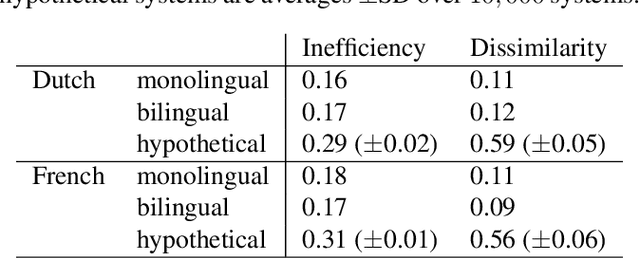
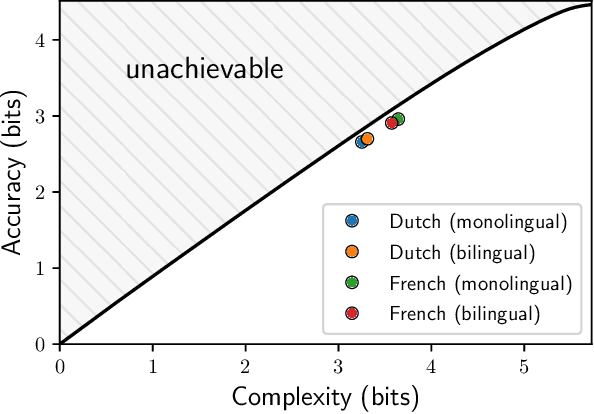
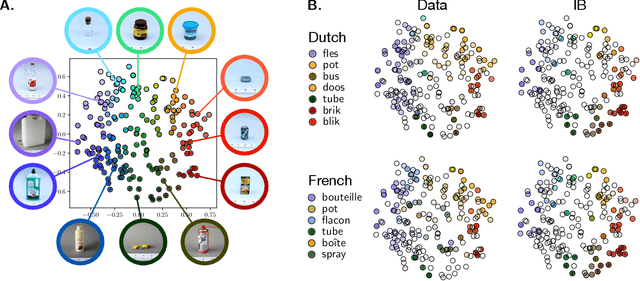
It has been argued that semantic categories across languages reflect pressure for efficient communication. Recently, this idea has been cast in terms of a general information-theoretic principle of efficiency, the Information Bottleneck (IB) principle, and it has been shown that this principle accounts for the emergence and evolution of named color categories across languages, including soft structure and patterns of inconsistent naming. However, it is not yet clear to what extent this account generalizes to semantic domains other than color. Here we show that it generalizes to two qualitatively different semantic domains: names for containers, and for animals. First, we show that container naming in Dutch and French is near-optimal in the IB sense, and that IB broadly accounts for soft categories and inconsistent naming patterns in both languages. Second, we show that a hierarchy of animal categories derived from IB captures cross-linguistic tendencies in the growth of animal taxonomies. Taken together, these findings suggest that fundamental information-theoretic principles of efficient coding may shape semantic categories across languages and across domains.

An Information-Theoretic Framework for Non-linear Canonical Correlation Analysis

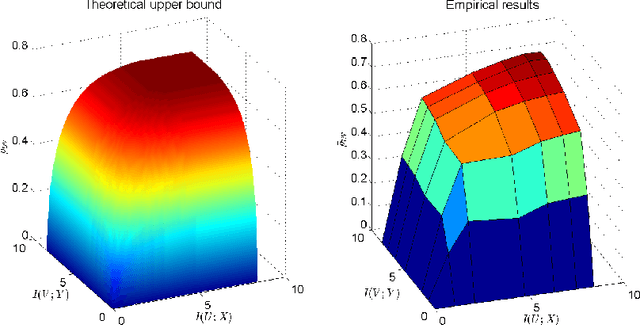
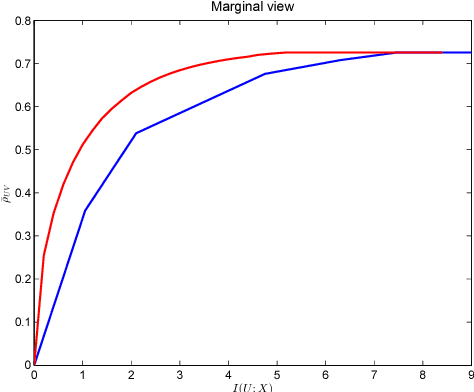
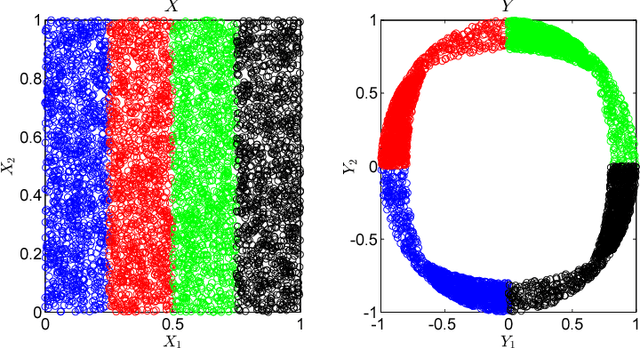
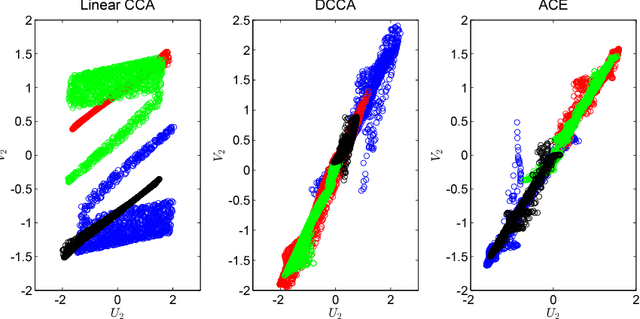
Canonical Correlation Analysis (CCA) is a linear representation learning method that seeks maximally correlated variables in multi-view data. Non-linear CCA extends this notion to a broader family of transformations, which are more powerful for many real-world applications. Given the joint probability, the Alternating Conditional Expectation (ACE) provides an optimal solution to the non-linear CCA problem. However, it suffers from limited performance and an increasing computational burden when only a finite number of observations is available. In this work we introduce an information-theoretic framework for the non-linear CCA problem (ITCCA), which extends the classical ACE approach. Our suggested framework seeks compressed representations of the data that allow a maximal level of correlation. This way we control the trade-off between the flexibility and the complexity of the representation. Our approach demonstrates favorable performance at a reduced computational burden, compared to non-linear alternatives, in a finite sample size regime. Further, ITCCA provides theoretical bounds and optimality conditions, as we establish fundamental connections to rate-distortion theory, the information bottleneck and remote source coding. In addition, it implies a "soft" dimensionality reduction, as the compression level is measured (and governed) by the mutual information between the original noisy data and the signals that we extract.

Efficient human-like semantic representations via the Information Bottleneck principle

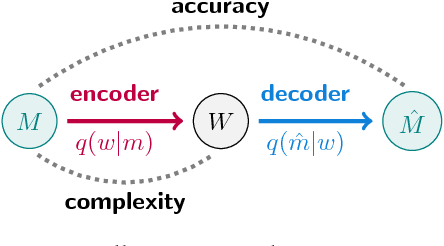
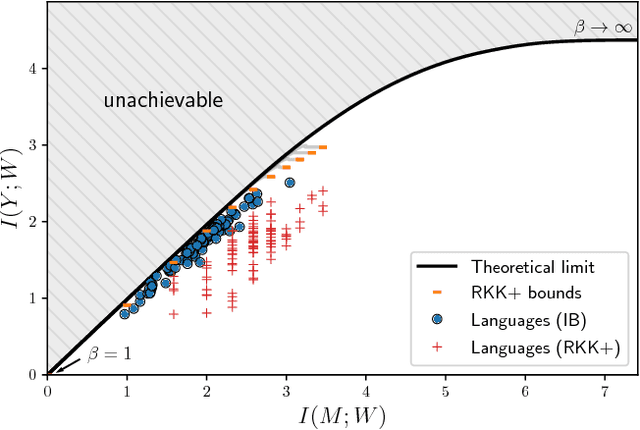
Maintaining efficient semantic representations of the environment is a major challenge both for humans and for machines. While human languages represent useful solutions to this problem, it is not yet clear what computational principle could give rise to similar solutions in machines. In this work we propose an answer to this open question. We suggest that languages compress percepts into words by optimizing the Information Bottleneck (IB) tradeoff between the complexity and accuracy of their lexicons. We present empirical evidence that this principle may give rise to human-like semantic representations, by exploring how human languages categorize colors. We show that color naming systems across languages are near-optimal in the IB sense, and that these natural systems are similar to artificial IB color naming systems with a single tradeoff parameter controlling the cross-language variability. In addition, the IB systems evolve through a sequence of structural phase transitions, demonstrating a possible adaptation process. This work thus identifies a computational principle that characterizes human semantic systems, and that could usefully inform semantic representations in machines.

Color naming reflects both perceptual structure and communicative need

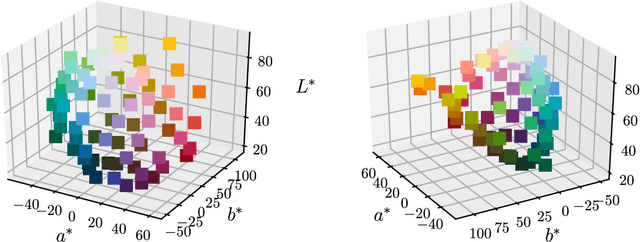
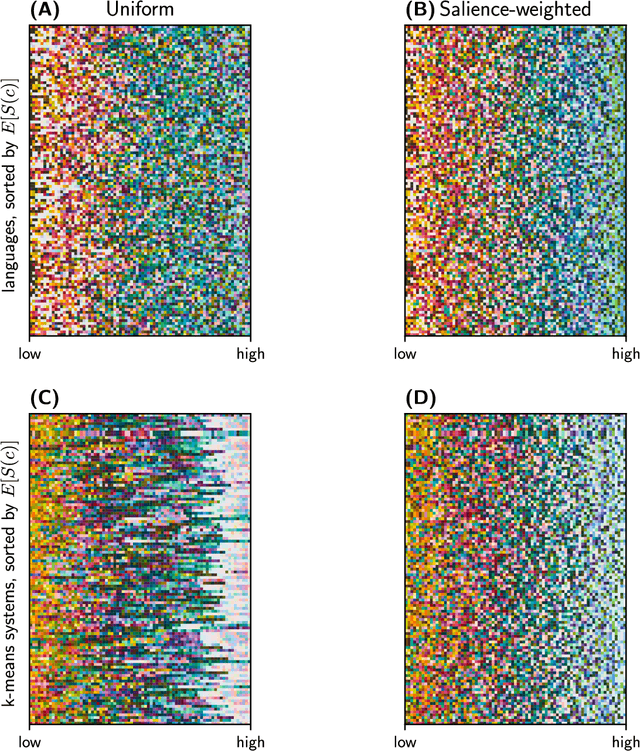
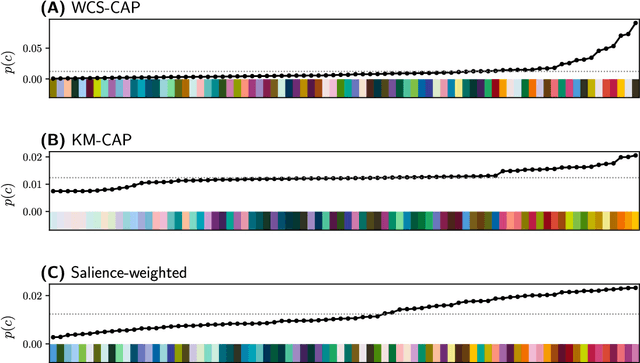
Gibson et al. (2017) argued that color naming is shaped by patterns of communicative need. In support of this claim, they showed that color naming systems across languages support more precise communication about warm colors than cool colors, and that the objects we talk about tend to be warm-colored rather than cool-colored. Here, we present new analyses that alter this picture. We show that greater communicative precision for warm than for cool colors, and greater communicative need, may both be explained by perceptual structure. However, using an information-theoretic analysis, we also show that color naming across languages bears signs of communicative need beyond what would be predicted by perceptual structure alone. We conclude that color naming is shaped both by perceptual structure, as has traditionally been argued, and by patterns of communicative need, as argued by Gibson et al. - although for reasons other than those they advanced.

A General Memory-Bounded Learning Algorithm

In an era of big data there is a growing need for memory-bounded learning algorithms. In the last few years researchers have investigated what cannot be learned under memory constraints. In this paper we focus on the complementary question of what can be learned under memory constraints. We show that if a hypothesis class fulfills a combinatorial condition defined in this paper, there is a memory-bounded learning algorithm for this class. We prove that certain natural classes fulfill this combinatorial property and thus can be learned under memory constraints.

Gaussian Lower Bound for the Information Bottleneck Limit

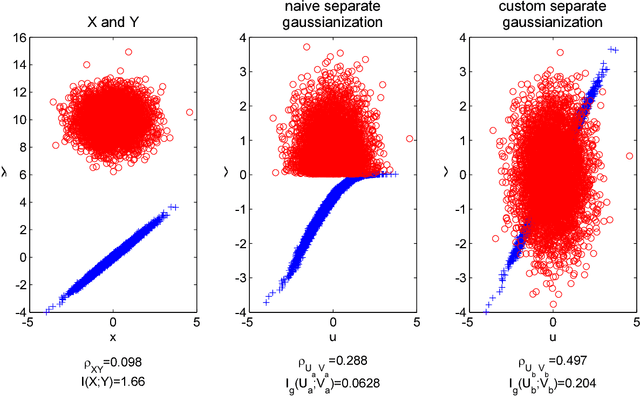
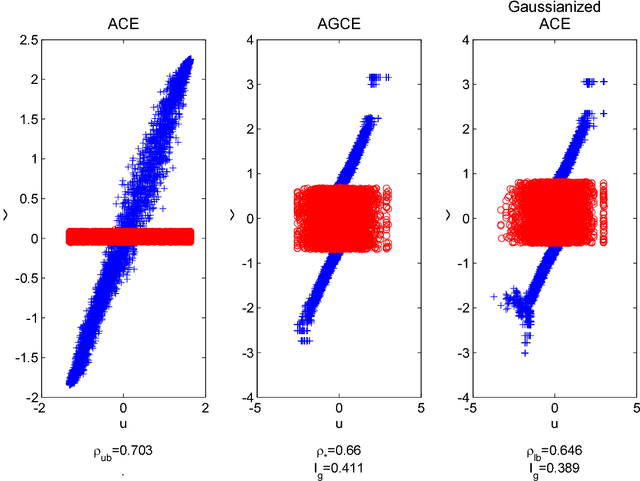
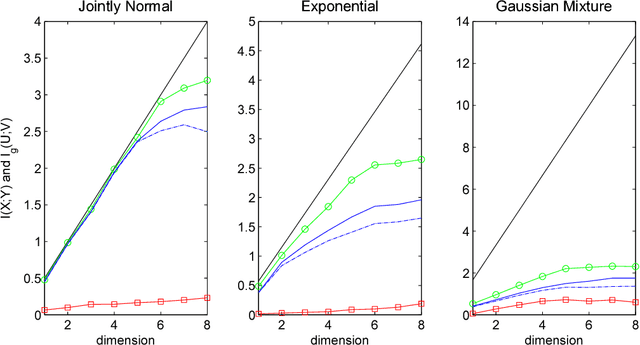
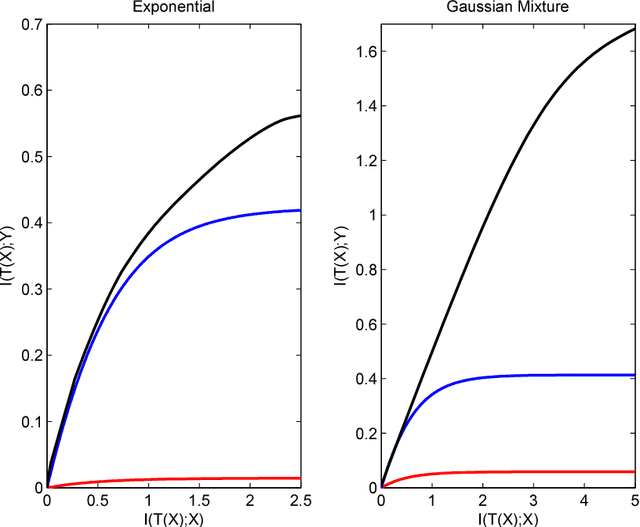
The Information Bottleneck (IB) is a conceptual method for extracting the most compact, yet informative, representation of a set of variables, with respect to the target. It generalizes the notion of minimal sufficient statistics from classical parametric statistics to a broader information-theoretic sense. The IB curve defines the optimal trade-off between representation complexity and its predictive power. Specifically, it is achieved by minimizing the level of mutual information (MI) between the representation and the original variables, subject to a minimal level of MI between the representation and the target. This problem is shown to be in general NP hard. One important exception is the multivariate Gaussian case, for which the Gaussian IB (GIB) is known to obtain an analytical closed form solution, similar to Canonical Correlation Analysis (CCA). In this work we introduce a Gaussian lower bound to the IB curve; we find an embedding of the data which maximizes its "Gaussian part", on which we apply the GIB. This embedding provides an efficient (and practical) representation of any arbitrary data-set (in the IB sense), which in addition holds the favorable properties of a Gaussian distribution. Importantly, we show that the optimal Gaussian embedding is bounded from above by non-linear CCA. This allows a fundamental limit for our ability to Gaussianize arbitrary data-sets and solve complex problems by linear methods.

Opening the Black Box of Deep Neural Networks via Information

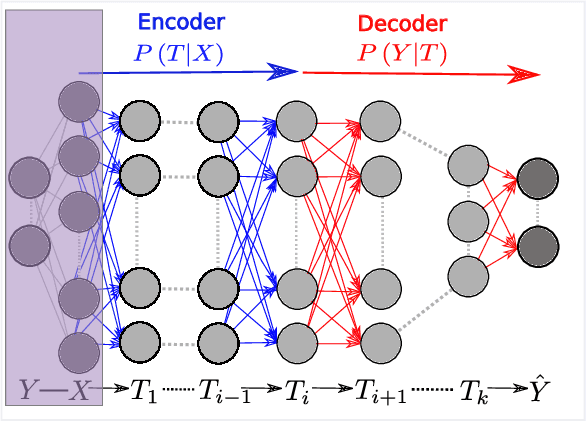
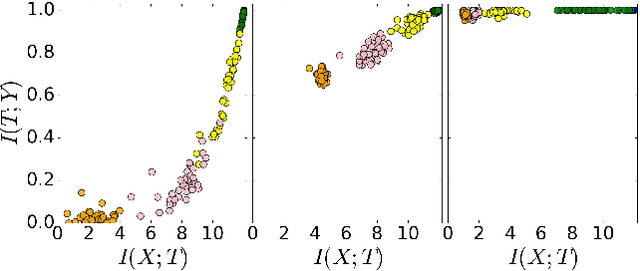
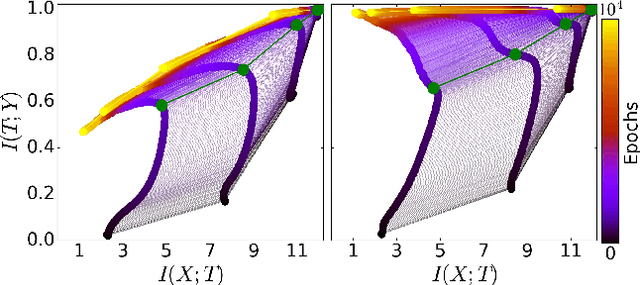
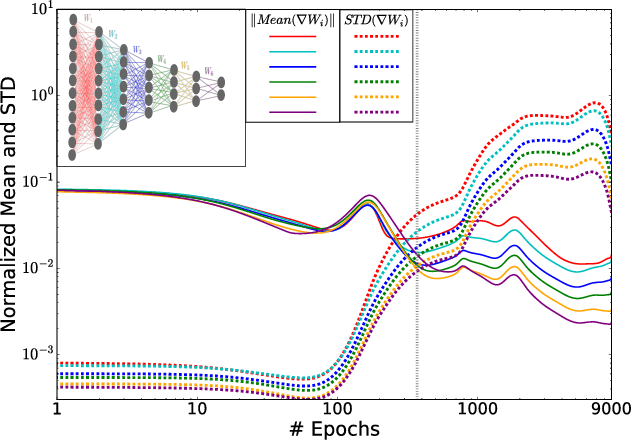
Despite their great success, there is still no comprehensive theoretical understanding of learning with Deep Neural Networks (DNNs) or their inner organization. Previous work proposed to analyze DNNs in the \textit{Information Plane}; i.e., the plane of the Mutual Information values that each layer preserves on the input and output variables. They suggested that the goal of the network is to optimize the Information Bottleneck (IB) tradeoff between compression and prediction, successively, for each layer. In this work we follow up on this idea and demonstrate the effectiveness of the Information-Plane visualization of DNNs. Our main results are: (i) most of the training epochs in standard DL are spent on {\emph compression} of the input to efficient representation and not on fitting the training labels. (ii) The representation compression phase begins when the training errors becomes small and the Stochastic Gradient Decent (SGD) epochs change from a fast drift to smaller training error into a stochastic relaxation, or random diffusion, constrained by the training error value. (iii) The converged layers lie on or very close to the Information Bottleneck (IB) theoretical bound, and the maps from the input to any hidden layer and from this hidden layer to the output satisfy the IB self-consistent equations. This generalization through noise mechanism is unique to Deep Neural Networks and absent in one layer networks. (iv) The training time is dramatically reduced when adding more hidden layers. Thus the main advantage of the hidden layers is computational. This can be explained by the reduced relaxation time, as this it scales super-linearly (exponentially for simple diffusion) with the information compression from the previous layer.