Learning force laws in many-body systems

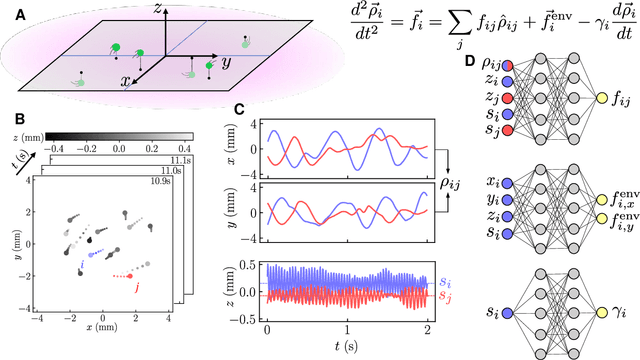
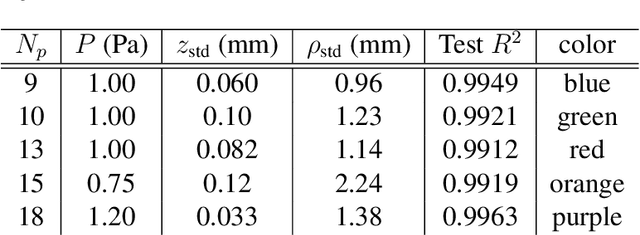
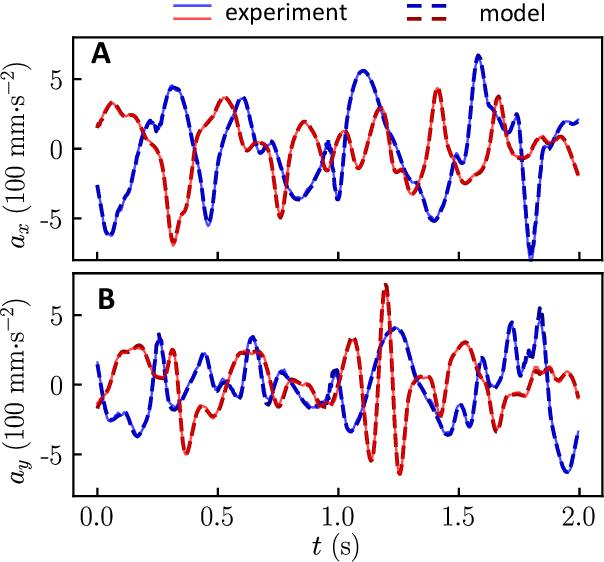
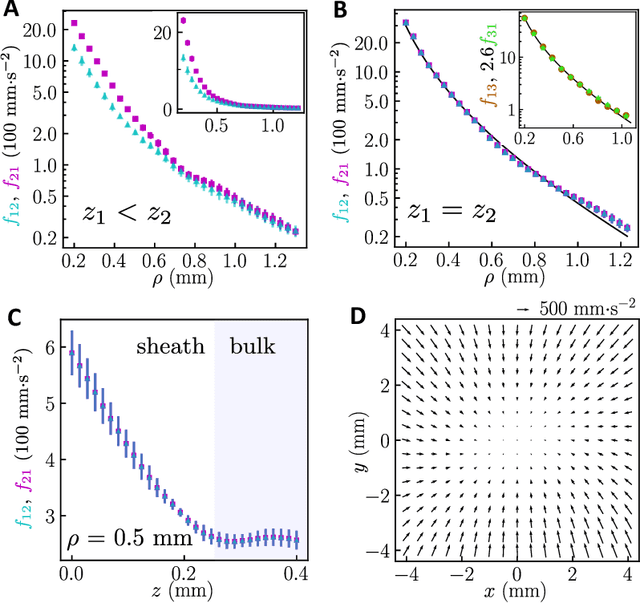
Scientific laws describing natural systems may be more complex than our intuition can handle, and thus how we discover laws must change. Machine learning (ML) models can analyze large quantities of data, but their structure should match the underlying physical constraints to provide useful insight. Here we demonstrate a ML approach that incorporates such physical intuition to infer force laws in dusty plasma experiments. Trained on 3D particle trajectories, the model accounts for inherent symmetries and non-identical particles, accurately learns the effective non-reciprocal forces between particles, and extracts each particle's mass and charge. The model's accuracy (R^2 > 0.99) points to new physics in dusty plasma beyond the resolution of current theories and demonstrates how ML-powered approaches can guide new routes of scientific discovery in many-body systems.

Simultaneous Dimensionality Reduction: A Data Efficient Approach for Multimodal Representations Learning

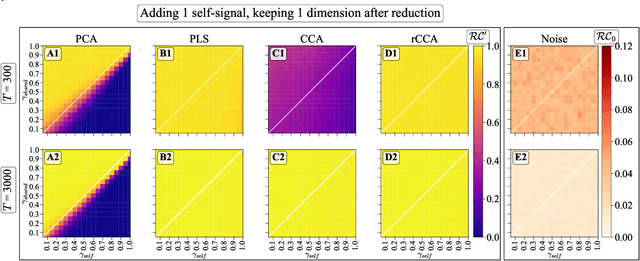
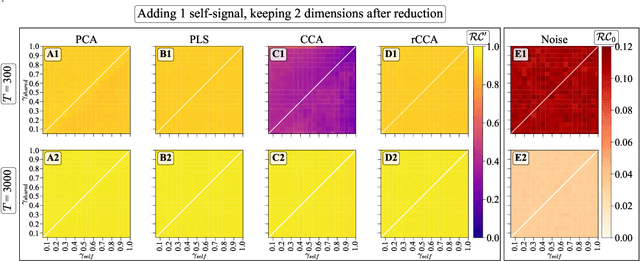
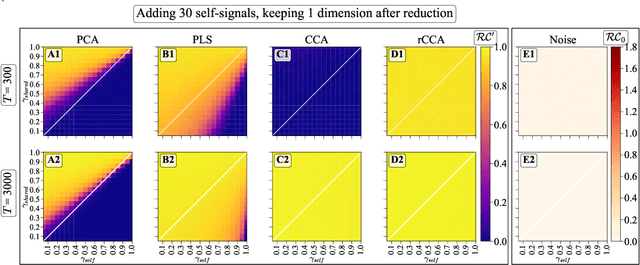
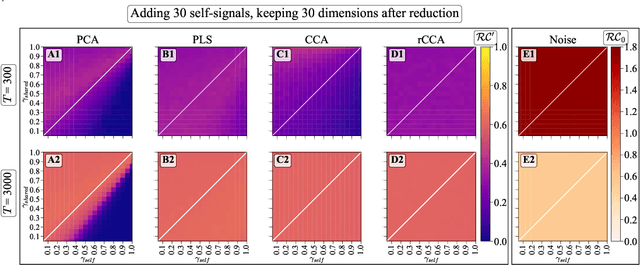
We explore two primary classes of approaches to dimensionality reduction (DR): Independent Dimensionality Reduction (IDR) and Simultaneous Dimensionality Reduction (SDR). In IDR methods, of which Principal Components Analysis is a paradigmatic example, each modality is compressed independently, striving to retain as much variation within each modality as possible. In contrast, in SDR, one simultaneously compresses the modalities to maximize the covariation between the reduced descriptions while paying less attention to how much individual variation is preserved. Paradigmatic examples include Partial Least Squares and Canonical Correlations Analysis. Even though these DR methods are a staple of statistics, their relative accuracy and data set size requirements are poorly understood. We introduce a generative linear model to synthesize multimodal data with known variance and covariance structures to examine these questions. We assess the accuracy of the reconstruction of the covariance structures as a function of the number of samples, signal-to-noise ratio, and the number of varying and covarying signals in the data. Using numerical experiments, we demonstrate that linear SDR methods consistently outperform linear IDR methods and yield higher-quality, more succinct reduced-dimensional representations with smaller datasets. Remarkably, regularized CCA can identify low-dimensional weak covarying structures even when the number of samples is much smaller than the dimensionality of the data, which is a regime challenging for all dimensionality reduction methods. Our work corroborates and explains previous observations in the literature that SDR can be more effective in detecting covariation patterns in data. These findings suggest that SDR should be preferred to IDR in real-world data analysis when detecting covariation is more important than preserving variation.

Deep Variational Multivariate Information Bottleneck -- A Framework for Variational Losses

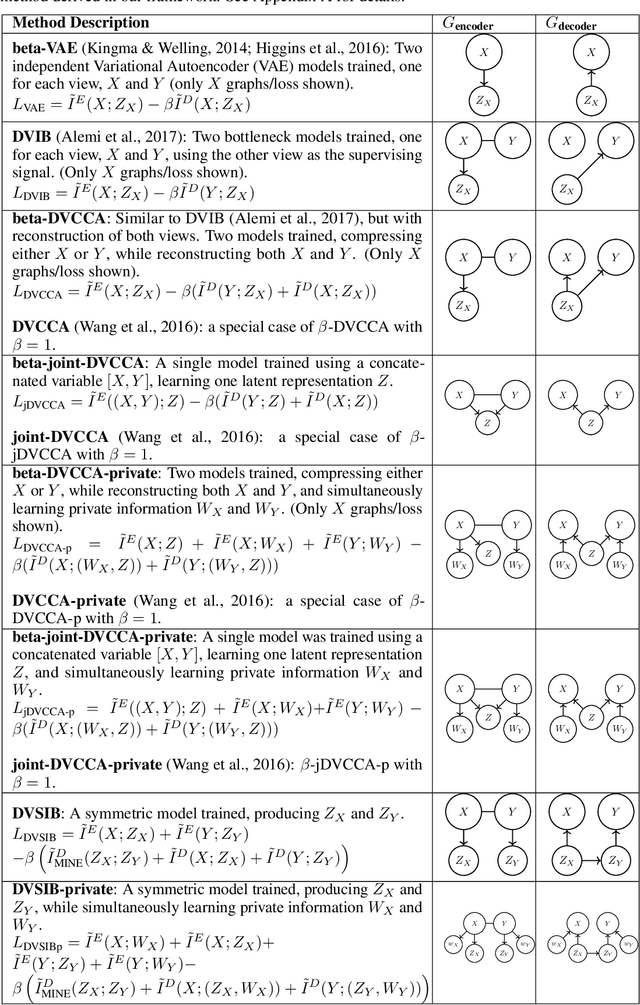
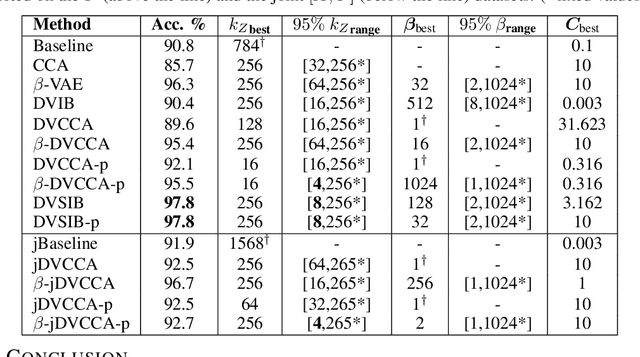
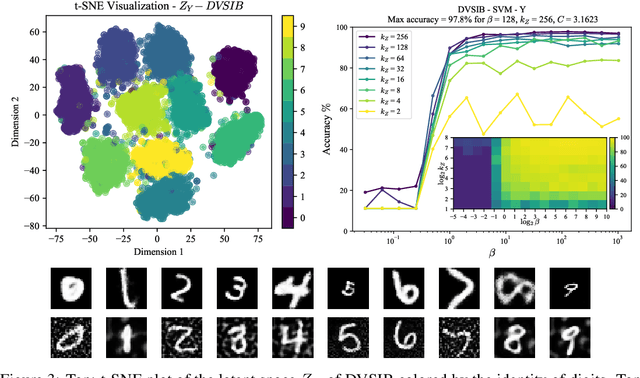
Variational dimensionality reduction methods are known for their high accuracy, generative abilities, and robustness. These methods have many theoretical justifications. Here we introduce a unifying principle rooted in information theory to rederive and generalize existing variational methods and design new ones. We base our framework on an interpretation of the multivariate information bottleneck, in which two Bayesian networks are traded off against one another. We interpret the first network as an encoder graph, which specifies what information to keep when compressing the data. We interpret the second network as a decoder graph, which specifies a generative model for the data. Using this framework, we rederive existing dimensionality reduction methods such as the deep variational information bottleneck (DVIB), beta variational auto-encoders (beta-VAE), and deep variational canonical correlation analysis (DVCCA). The framework naturally introduces a trade-off parameter between compression and reconstruction in the DVCCA family of algorithms, resulting in the new beta-DVCCA family. In addition, we derive a new variational dimensionality reduction method, deep variational symmetric informational bottleneck (DVSIB), which simultaneously compresses two variables to preserve information between their compressed representations. We implement all of these algorithms and evaluate their ability to produce shared low dimensional latent spaces on a modified noisy MNIST dataset. We show that algorithms that are better matched to the structure of the data (beta-DVCCA and DVSIB) produce better latent spaces as measured by classification accuracy and the dimensionality of the latent variables. We believe that this framework can be used to unify other multi-view representation learning algorithms. Additionally, it provides a straightforward framework for deriving problem-specific loss functions.

Data efficiency, dimensionality reduction, and the generalized symmetric information bottleneck

The Symmetric Information Bottleneck (SIB), an extension of the more familiar Information Bottleneck, is a dimensionality reduction technique that simultaneously compresses two random variables to preserve information between their compressed versions. We introduce the Generalized Symmetric Information Bottleneck (GSIB), which explores different functional forms of the cost of such simultaneous reduction. We then explore the dataset size requirements of such simultaneous compression. We do this by deriving bounds and root-mean-squared estimates of statistical fluctuations of the involved loss functions. We show that, in typical situations, the simultaneous GSIB compression requires qualitatively less data to achieve the same errors compared to compressing variables one at a time. We suggest that this is an example of a more general principle that simultaneous compression is more data efficient than independent compression of each of the input variables.

Inferring Local Structure from Pairwise Correlations

To construct models of large, multivariate complex systems, such as those in biology, one needs to constrain which variables are allowed to interact. This can be viewed as detecting ``local'' structures among the variables. In the context of a simple toy model of 2D natural and synthetic images, we show that pairwise correlations between the variables -- even when severely undersampled -- provide enough information to recover local relations, including the dimensionality of the data, and to reconstruct arrangement of pixels in fully scrambled images. This proves to be successful even though higher order interaction structures are present in our data. We build intuition behind the success, which we hope might contribute to modeling complex, multivariate systems and to explaining the success of modern attention-based machine learning approaches.

Intrinsic Motivation in Dynamical Control Systems

Biological systems often choose actions without an explicit reward signal, a phenomenon known as intrinsic motivation. The computational principles underlying this behavior remain poorly understood. In this study, we investigate an information-theoretic approach to intrinsic motivation, based on maximizing an agent's empowerment (the mutual information between its past actions and future states). We show that this approach generalizes previous attempts to formalize intrinsic motivation, and we provide a computationally efficient algorithm for computing the necessary quantities. We test our approach on several benchmark control problems, and we explain its success in guiding intrinsically motivated behaviors by relating our information-theoretic control function to fundamental properties of the dynamical system representing the combined agent-environment system. This opens the door for designing practical artificial, intrinsically motivated controllers and for linking animal behaviors to their dynamical properties.

Automated, predictive, and interpretable inference of C. elegans escape dynamics

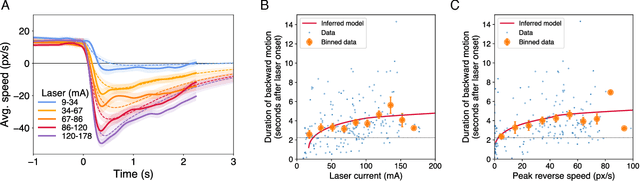
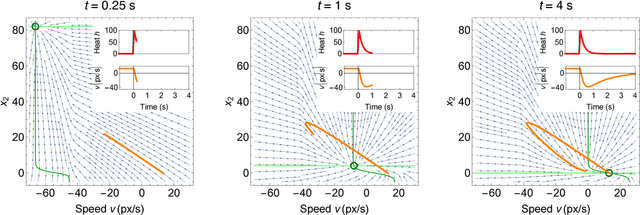
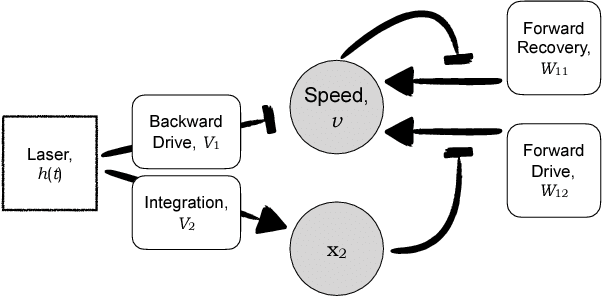
The roundworm C. elegans exhibits robust escape behavior in response to rapidly rising temperature. The behavior lasts for a few seconds, shows history dependence, involves both sensory and motor systems, and is too complicated to model mechanistically using currently available knowledge. Instead we model the process phenomenologically, and we use the Sir Isaac dynamical inference platform to infer the model in a fully automated fashion directly from experimental data. The inferred model requires incorporation of an unobserved dynamical variable, and is biologically interpretable. The model makes accurate predictions about the dynamics of the worm behavior, and it can be used to characterize the functional logic of the dynamical system underlying the escape response. This work illustrates the power of modern artificial intelligence to aid in discovery of accurate and interpretable models of complex natural systems.

Director Field Model of the Primary Visual Cortex for Contour Detection

We aim to build the simplest possible model capable of detecting long, noisy contours in a cluttered visual scene. For this, we model the neural dynamics in the primate primary visual cortex in terms of a continuous director field that describes the average rate and the average orientational preference of active neurons at a particular point in the cortex. We then use a linear-nonlinear dynamical model with long range connectivity patterns to enforce long-range statistical context present in the analyzed images. The resulting model has substantially fewer degrees of freedom than traditional models, and yet it can distinguish large contiguous objects from the background clutter by suppressing the clutter and by filling-in occluded elements of object contours. This results in high-precision, high-recall detection of large objects in cluttered scenes. Parenthetically, our model has a direct correspondence with the Landau - de Gennes theory of nematic liquid crystal in two dimensions.

Automated adaptive inference of coarse-grained dynamical models in systems biology

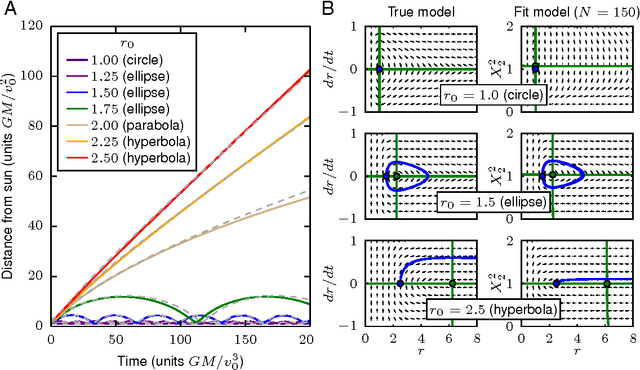
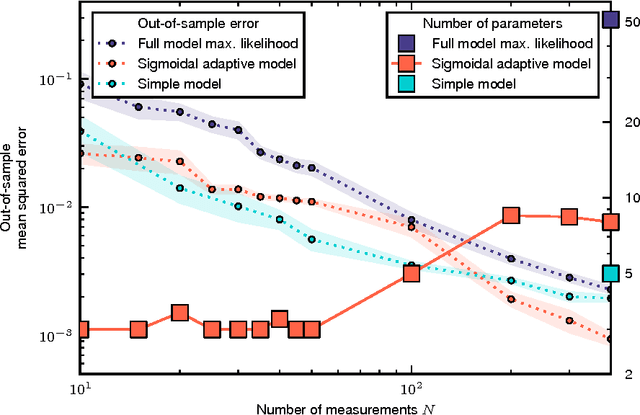
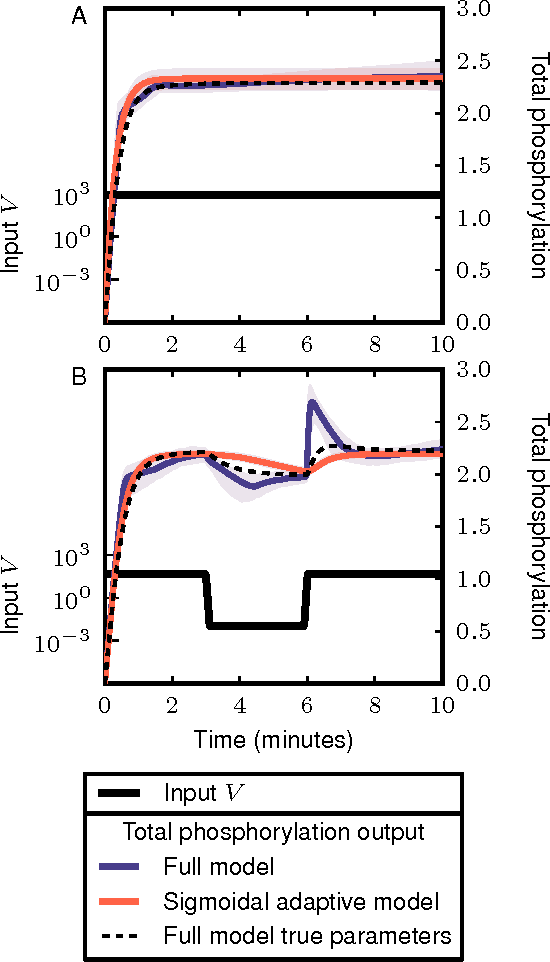
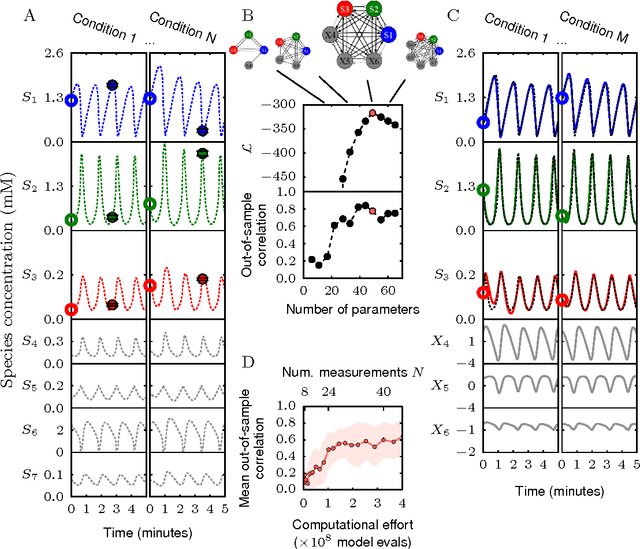
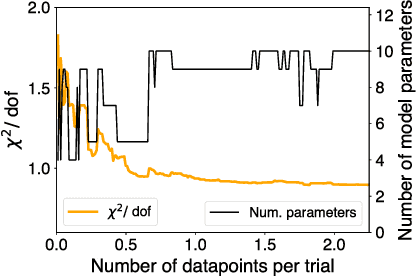
Cellular regulatory dynamics is driven by large and intricate networks of interactions at the molecular scale, whose sheer size obfuscates understanding. In light of limited experimental data, many parameters of such dynamics are unknown, and thus models built on the detailed, mechanistic viewpoint overfit and are not predictive. At the other extreme, simple ad hoc models of complex processes often miss defining features of the underlying systems. Here we propose an approach that instead constructs phenomenological, coarse-grained models of network dynamics that automatically adapt their complexity to the amount of available data. Such adaptive models lead to accurate predictions even when microscopic details of the studied systems are unknown due to insufficient data. The approach is computationally tractable, even for a relatively large number of dynamical variables, allowing its software realization, named Sir Isaac, to make successful predictions even when important dynamic variables are unobserved. For example, it matches the known phase space structure for simulated planetary motion data, avoids overfitting in a complex biological signaling system, and produces accurate predictions for a yeast glycolysis model with only tens of data points and over half of the interacting species unobserved.

Fluctuation-dissipation theorem and models of learning

Advances in statistical learning theory have resulted in a multitude of different designs of learning machines. But which ones are implemented by brains and other biological information processors? We analyze how various abstract Bayesian learners perform on different data and argue that it is difficult to determine which learning-theoretic computation is performed by a particular organism using just its performance in learning a stationary target (learning curve). Basing on the fluctuation-dissipation relation in statistical physics, we then discuss a different experimental setup that might be able to solve the problem.