Goals and the Structure of Experience

Purposeful behavior is a hallmark of natural and artificial intelligence. Its acquisition is often believed to rely on world models, comprising both descriptive (what is) and prescriptive (what is desirable) aspects that identify and evaluate state of affairs in the world, respectively. Canonical computational accounts of purposeful behavior, such as reinforcement learning, posit distinct components of a world model comprising a state representation (descriptive aspect) and a reward function (prescriptive aspect). However, an alternative possibility, which has not yet been computationally formulated, is that these two aspects instead co-emerge interdependently from an agent's goal. Here, we describe a computational framework of goal-directed state representation in cognitive agents, in which the descriptive and prescriptive aspects of a world model co-emerge from agent-environment interaction sequences, or experiences. Drawing on Buddhist epistemology, we introduce a construct of goal-directed, or telic, states, defined as classes of goal-equivalent experience distributions. Telic states provide a parsimonious account of goal-directed learning in terms of the statistical divergence between behavioral policies and desirable experience features. We review empirical and theoretical literature supporting this novel perspective and discuss its potential to provide a unified account of behavioral, phenomenological and neural dimensions of purposeful behaviors across diverse substrates.

Decentralized Traffic Flow Optimization Through Intrinsic Motivation

Traffic congestion has long been an ubiquitous problem that is exacerbating with the rapid growth of megacities. In this proof-of-concept work we study intrinsic motivation, implemented via the empowerment principle, to control autonomous car behavior to improve traffic flow. In standard models of traffic dynamics, self-organized traffic jams emerge spontaneously from the individual behavior of cars, affecting traffic over long distances. Our novel car behavior strategy improves traffic flow while still being decentralized and using only locally available information without explicit coordination. Decentralization is essential for various reasons, not least to be able to absorb robustly substantial levels of uncertainty. Our scenario is based on the well-established traffic dynamics model, the Nagel-Schreckenberg cellular automaton. In a fraction of the cars in this model, we substitute the default behavior by empowerment, our intrinsic motivation-based method. This proposed model significantly improves overall traffic flow, mitigates congestion, and reduces the average traffic jam time.

Acoustic Wave Manipulation Through Sparse Robotic Actuation

Recent advancements in robotics, control, and machine learning have facilitated progress in the challenging area of object manipulation. These advancements include, among others, the use of deep neural networks to represent dynamics that are partially observed by robot sensors, as well as effective control using sparse control signals. In this work, we explore a more general problem: the manipulation of acoustic waves, which are partially observed by a robot capable of influencing the waves through spatially sparse actuators. This problem holds great potential for the design of new artificial materials, ultrasonic cutting tools, energy harvesting, and other applications. We develop an efficient data-driven method for robot learning that is applicable to either focusing scattered acoustic energy in a designated region or suppressing it, depending on the desired task. The proposed method is better in terms of a solution quality and computational complexity as compared to a state-of-the-art learning based method for manipulation of dynamical systems governed by partial differential equations. Furthermore our proposed method is competitive with a classical semi-analytical method in acoustics research on the demonstrated tasks. We have made the project code publicly available, along with a web page featuring video demonstrations: https://gladisor.github.io/waves/.

EVAL: EigenVector-based Average-reward Learning

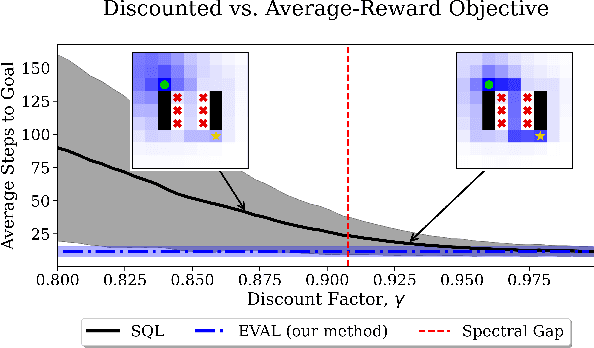
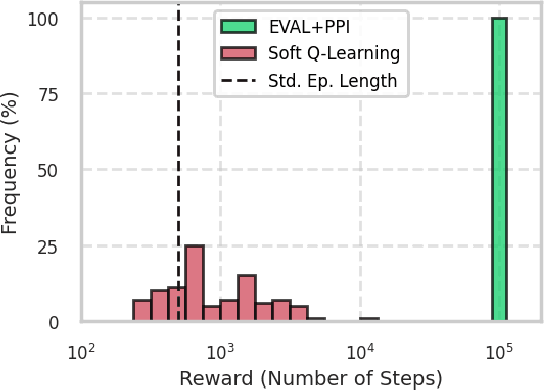
In reinforcement learning, two objective functions have been developed extensively in the literature: discounted and averaged rewards. The generalization to an entropy-regularized setting has led to improved robustness and exploration for both of these objectives. Recently, the entropy-regularized average-reward problem was addressed using tools from large deviation theory in the tabular setting. This method has the advantage of linearity, providing access to both the optimal policy and average reward-rate through properties of a single matrix. In this paper, we extend that framework to more general settings by developing approaches based on function approximation by neural networks. This formulation reveals new theoretical insights into the relationship between different objectives used in RL. Additionally, we combine our algorithm with a posterior policy iteration scheme, showing how our approach can also solve the average-reward RL problem without entropy-regularization. Using classic control benchmarks, we experimentally find that our method compares favorably with other algorithms in terms of stability and rate of convergence.

Bootstrapped Reward Shaping

In reinforcement learning, especially in sparse-reward domains, many environment steps are required to observe reward information. In order to increase the frequency of such observations, "potential-based reward shaping" (PBRS) has been proposed as a method of providing a more dense reward signal while leaving the optimal policy invariant. However, the required "potential function" must be carefully designed with task-dependent knowledge to not deter training performance. In this work, we propose a "bootstrapped" method of reward shaping, termed BSRS, in which the agent's current estimate of the state-value function acts as the potential function for PBRS. We provide convergence proofs for the tabular setting, give insights into training dynamics for deep RL, and show that the proposed method improves training speed in the Atari suite.

SuPLE: Robot Learning with Lyapunov Rewards

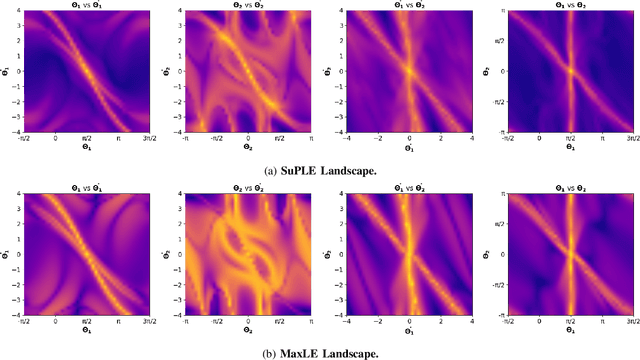
The reward function is an essential component in robot learning. Reward directly affects the sample and computational complexity of learning, and the quality of a solution. The design of informative rewards requires domain knowledge, which is not always available. We use the properties of the dynamics to produce system-appropriate reward without adding external assumptions. Specifically, we explore an approach to utilize the Lyapunov exponents of the system dynamics to generate a system-immanent reward. We demonstrate that the `Sum of the Positive Lyapunov Exponents' (SuPLE) is a strong candidate for the design of such a reward. We develop a computational framework for the derivation of this reward, and demonstrate its effectiveness on classical benchmarks for sample-based stabilization of various dynamical systems. It eliminates the need to start the training trajectories at arbitrary states, also known as auxiliary exploration. While the latter is a common practice in simulated robot learning, it is unpractical to consider to use it in real robotic systems, since they typically start from natural rest states such as a pendulum at the bottom, a robot on the ground, etc. and can not be easily initialized at arbitrary states. Comparing the performance of SuPLE to commonly-used reward functions, we observe that the latter fail to find a solution without auxiliary exploration, even for the task of swinging up the double pendulum and keeping it stable at the upright position, a prototypical scenario for multi-linked robots. SuPLE-induced rewards for robot learning offer a novel route for effective robot learning in typical as opposed to highly specialized or fine-tuned scenarios. Our code is publicly available for reproducibility and further research.

Boosting Soft Q-Learning by Bounding

An agent's ability to leverage past experience is critical for efficiently solving new tasks. Prior work has focused on using value function estimates to obtain zero-shot approximations for solutions to a new task. In soft Q-learning, we show how any value function estimate can also be used to derive double-sided bounds on the optimal value function. The derived bounds lead to new approaches for boosting training performance which we validate experimentally. Notably, we find that the proposed framework suggests an alternative method for updating the Q-function, leading to boosted performance.

Learning telic-controllable state representations

Computational accounts of purposeful behavior consist of descriptive and normative aspects. The former enable agents to ascertain the current (or future) state of affairs in the world and the latter to evaluate the desirability, or lack thereof, of these states with respect to the agent's goals. In Reinforcement Learning, the normative aspect (reward and value functions) is assumed to depend on a pre-defined and fixed descriptive one (state representation). Alternatively, these two aspects may emerge interdependently: goals can be, and indeed often are, expressed in terms of state representation features, but they may also serve to shape state representations themselves. Here, we illustrate a novel theoretical framing of state representation learning in bounded agents, coupling descriptive and normative aspects via the notion of goal-directed, or telic, states. We define a new controllability property of telic state representations to characterize the tradeoff between their granularity and the policy complexity capacity required to reach all telic states. We propose an algorithm for learning controllable state representations and demonstrate it using a simple navigation task with changing goals. Our framework highlights the crucial role of deliberate ignorance - knowing what to ignore - for learning state representations that are both goal-flexible and simple. More broadly, our work provides a concrete step towards a unified theoretical view of natural and artificial learning through the lens of goals.

Multi-Resolution Diffusion for Privacy-Sensitive Recommender Systems

While recommender systems have become an integral component of the Web experience, their heavy reliance on user data raises privacy and security concerns. Substituting user data with synthetic data can address these concerns, but accurately replicating these real-world datasets has been a notoriously challenging problem. Recent advancements in generative AI have demonstrated the impressive capabilities of diffusion models in generating realistic data across various domains. In this work we introduce a Score-based Diffusion Recommendation Module (SDRM), which captures the intricate patterns of real-world datasets required for training highly accurate recommender systems. SDRM allows for the generation of synthetic data that can replace existing datasets to preserve user privacy, or augment existing datasets to address excessive data sparsity. Our method outperforms competing baselines such as generative adversarial networks, variational autoencoders, and recently proposed diffusion models in synthesizing various datasets to replace or augment the original data by an average improvement of 4.30% in Recall@$k$ and 4.65% in NDCG@$k$.

Dimensionality Reduction of Dynamics on Lie Manifolds via Structure-Aware Canonical Correlation Analysis

Incorporating prior knowledge into a data-driven modeling problem can drastically improve performance, reliability, and generalization outside of the training sample. The stronger the structural properties, the more effective these improvements become. Manifolds are a powerful nonlinear generalization of Euclidean space for modeling finite dimensions. Structural impositions in constrained systems increase when applying group structure, converting them into Lie manifolds. The range of their applications is very wide and includes the important case of robotic tasks. Canonical Correlation Analysis (CCA) can construct a hierarchical sequence of maximal correlations of up to two paired data sets in these Euclidean spaces. We present a method to generalize this concept to Lie Manifolds and demonstrate its efficacy through the substantial improvements it achieves in making structure-consistent predictions about changes in the state of a robotic hand.