Inferring Transition Dynamics from Value Functions

In reinforcement learning, the value function is typically trained to solve the Bellman equation, which connects the current value to future values. This temporal dependency hints that the value function may contain implicit information about the environment's transition dynamics. By rearranging the Bellman equation, we show that a converged value function encodes a model of the underlying dynamics of the environment. We build on this insight to propose a simple method for inferring dynamics models directly from the value function, potentially mitigating the need for explicit model learning. Furthermore, we explore the challenges of next-state identifiability, discussing conditions under which the inferred dynamics model is well-defined. Our work provides a theoretical foundation for leveraging value functions in dynamics modeling and opens a new avenue for bridging model-free and model-based reinforcement learning.

EVAL: EigenVector-based Average-reward Learning

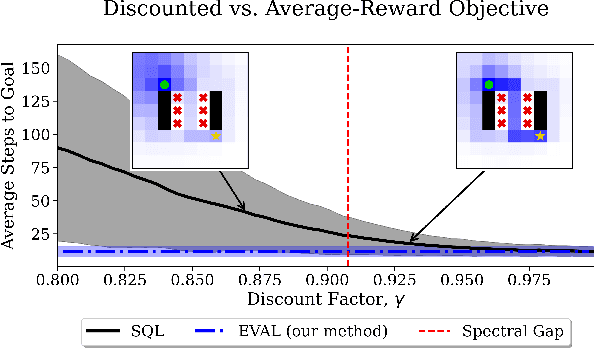
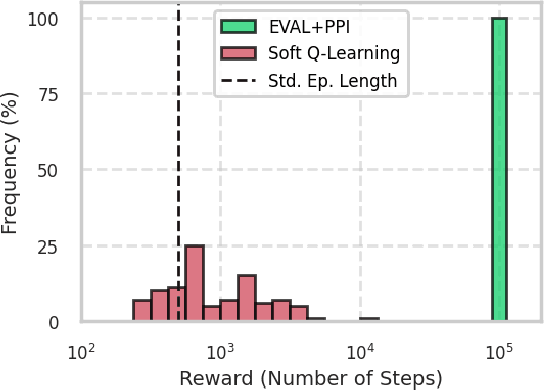
In reinforcement learning, two objective functions have been developed extensively in the literature: discounted and averaged rewards. The generalization to an entropy-regularized setting has led to improved robustness and exploration for both of these objectives. Recently, the entropy-regularized average-reward problem was addressed using tools from large deviation theory in the tabular setting. This method has the advantage of linearity, providing access to both the optimal policy and average reward-rate through properties of a single matrix. In this paper, we extend that framework to more general settings by developing approaches based on function approximation by neural networks. This formulation reveals new theoretical insights into the relationship between different objectives used in RL. Additionally, we combine our algorithm with a posterior policy iteration scheme, showing how our approach can also solve the average-reward RL problem without entropy-regularization. Using classic control benchmarks, we experimentally find that our method compares favorably with other algorithms in terms of stability and rate of convergence.

Bootstrapped Reward Shaping

In reinforcement learning, especially in sparse-reward domains, many environment steps are required to observe reward information. In order to increase the frequency of such observations, "potential-based reward shaping" (PBRS) has been proposed as a method of providing a more dense reward signal while leaving the optimal policy invariant. However, the required "potential function" must be carefully designed with task-dependent knowledge to not deter training performance. In this work, we propose a "bootstrapped" method of reward shaping, termed BSRS, in which the agent's current estimate of the state-value function acts as the potential function for PBRS. We provide convergence proofs for the tabular setting, give insights into training dynamics for deep RL, and show that the proposed method improves training speed in the Atari suite.

Reinforcement Learning for Control of Non-Markovian Cellular Population Dynamics

Many organisms and cell types, from bacteria to cancer cells, exhibit a remarkable ability to adapt to fluctuating environments. Additionally, cells can leverage memory of past environments to better survive previously-encountered stressors. From a control perspective, this adaptability poses significant challenges in driving cell populations toward extinction, and is thus an open question with great clinical significance. In this work, we focus on drug dosing in cell populations exhibiting phenotypic plasticity. For specific dynamical models switching between resistant and susceptible states, exact solutions are known. However, when the underlying system parameters are unknown, and for complex memory-based systems, obtaining the optimal solution is currently intractable. To address this challenge, we apply reinforcement learning (RL) to identify informed dosing strategies to control cell populations evolving under novel non-Markovian dynamics. We find that model-free deep RL is able to recover exact solutions and control cell populations even in the presence of long-range temporal dynamics.

Boosting Soft Q-Learning by Bounding

An agent's ability to leverage past experience is critical for efficiently solving new tasks. Prior work has focused on using value function estimates to obtain zero-shot approximations for solutions to a new task. In soft Q-learning, we show how any value function estimate can also be used to derive double-sided bounds on the optimal value function. The derived bounds lead to new approaches for boosting training performance which we validate experimentally. Notably, we find that the proposed framework suggests an alternative method for updating the Q-function, leading to boosted performance.

Bounding the Optimal Value Function in Compositional Reinforcement Learning

In the field of reinforcement learning (RL), agents are often tasked with solving a variety of problems differing only in their reward functions. In order to quickly obtain solutions to unseen problems with new reward functions, a popular approach involves functional composition of previously solved tasks. However, previous work using such functional composition has primarily focused on specific instances of composition functions whose limiting assumptions allow for exact zero-shot composition. Our work unifies these examples and provides a more general framework for compositionality in both standard and entropy-regularized RL. We find that, for a broad class of functions, the optimal solution for the composite task of interest can be related to the known primitive task solutions. Specifically, we present double-sided inequalities relating the optimal composite value function to the value functions for the primitive tasks. We also show that the regret of using a zero-shot policy can be bounded for this class of functions. The derived bounds can be used to develop clipping approaches for reducing uncertainty during training, allowing agents to quickly adapt to new tasks.

Compositionality and Bounds for Optimal Value Functions in Reinforcement Learning

An agent's ability to reuse solutions to previously solved problems is critical for learning new tasks efficiently. Recent research using composition of value functions in reinforcement learning has shown that agents can utilize solutions of primitive tasks to obtain solutions for exponentially many new tasks. However, previous work has relied on restrictive assumptions on the dynamics, the method of composition, and the structure of reward functions. Here we consider the case of general composition functions without any restrictions on the structure of reward functions, applicable to both deterministic and stochastic dynamics. For this general setup, we provide bounds on the corresponding optimal value functions and characterize the value of corresponding policies. The theoretical results derived lead to improvements in training for both entropy-regularized and standard reinforcement learning, which we validate with numerical simulations.

Utilizing Prior Solutions for Reward Shaping and Composition in Entropy-Regularized Reinforcement Learning

In reinforcement learning (RL), the ability to utilize prior knowledge from previously solved tasks can allow agents to quickly solve new problems. In some cases, these new problems may be approximately solved by composing the solutions of previously solved primitive tasks (task composition). Otherwise, prior knowledge can be used to adjust the reward function for a new problem, in a way that leaves the optimal policy unchanged but enables quicker learning (reward shaping). In this work, we develop a general framework for reward shaping and task composition in entropy-regularized RL. To do so, we derive an exact relation connecting the optimal soft value functions for two entropy-regularized RL problems with different reward functions and dynamics. We show how the derived relation leads to a general result for reward shaping in entropy-regularized RL. We then generalize this approach to derive an exact relation connecting optimal value functions for the composition of multiple tasks in entropy-regularized RL. We validate these theoretical contributions with experiments showing that reward shaping and task composition lead to faster learning in various settings.

Neural Network Degeneration and its Relationship to the Brain

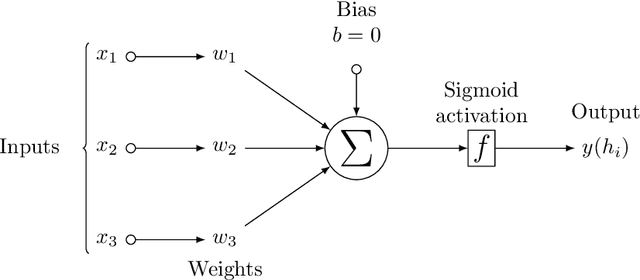
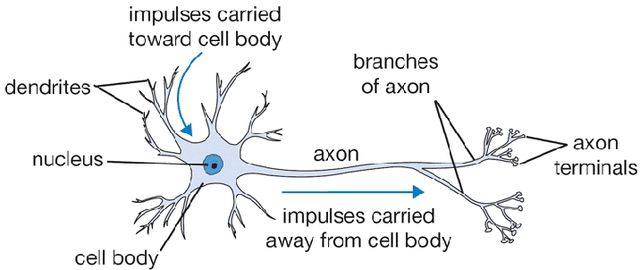
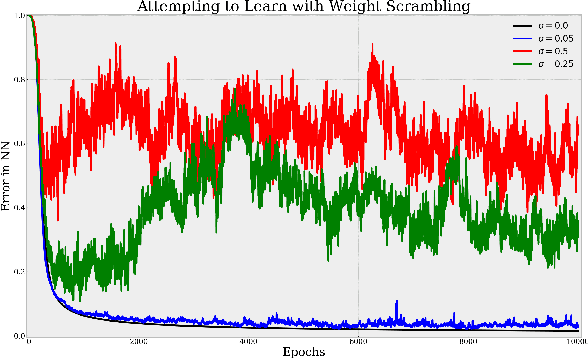
This report discusses the application of neural networks (NNs) as small segments of the brain. The networks representing the biological connectome are altered both spatially and temporally. The degradation techniques applied here are "weight degradation", "weight scrambling", and variable activation function. These methods aim to shine light on the study of neurodegenerative diseases such as Alzheimer's, Huntington's and Parkinson's disease as well as strokes and brain tumors disrupting the flow of information in the brain's network. Fundamental insights to memory loss and generalized learning dysfunction are gained by monitoring the network's error function during network degradation. The biological significance of each facet is also discussed.