Bounding the Optimal Value Function in Compositional Reinforcement Learning

In the field of reinforcement learning (RL), agents are often tasked with solving a variety of problems differing only in their reward functions. In order to quickly obtain solutions to unseen problems with new reward functions, a popular approach involves functional composition of previously solved tasks. However, previous work using such functional composition has primarily focused on specific instances of composition functions whose limiting assumptions allow for exact zero-shot composition. Our work unifies these examples and provides a more general framework for compositionality in both standard and entropy-regularized RL. We find that, for a broad class of functions, the optimal solution for the composite task of interest can be related to the known primitive task solutions. Specifically, we present double-sided inequalities relating the optimal composite value function to the value functions for the primitive tasks. We also show that the regret of using a zero-shot policy can be bounded for this class of functions. The derived bounds can be used to develop clipping approaches for reducing uncertainty during training, allowing agents to quickly adapt to new tasks.

Utilizing Prior Solutions for Reward Shaping and Composition in Entropy-Regularized Reinforcement Learning

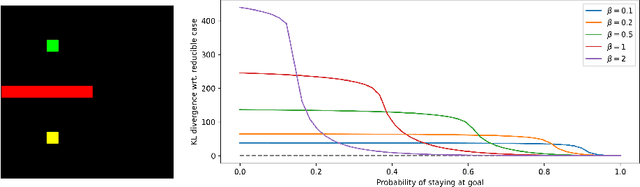
In reinforcement learning (RL), the ability to utilize prior knowledge from previously solved tasks can allow agents to quickly solve new problems. In some cases, these new problems may be approximately solved by composing the solutions of previously solved primitive tasks (task composition). Otherwise, prior knowledge can be used to adjust the reward function for a new problem, in a way that leaves the optimal policy unchanged but enables quicker learning (reward shaping). In this work, we develop a general framework for reward shaping and task composition in entropy-regularized RL. To do so, we derive an exact relation connecting the optimal soft value functions for two entropy-regularized RL problems with different reward functions and dynamics. We show how the derived relation leads to a general result for reward shaping in entropy-regularized RL. We then generalize this approach to derive an exact relation connecting optimal value functions for the composition of multiple tasks in entropy-regularized RL. We validate these theoretical contributions with experiments showing that reward shaping and task composition lead to faster learning in various settings.

Closed-Form Analytical Results for Maximum Entropy Reinforcement Learning

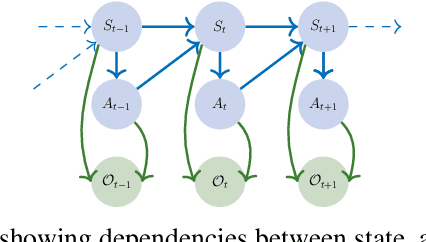
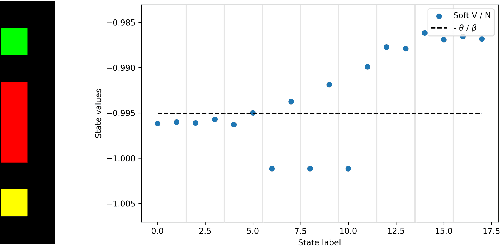
We introduce a mapping between Maximum Entropy Reinforcement Learning (MaxEnt RL) and Markovian processes conditioned on rare events. In the long time limit, this mapping allows us to derive analytical expressions for the optimal policy, dynamics and initial state distributions for the general case of stochastic dynamics in MaxEnt RL. We find that soft-$\mathcal{Q}$ functions in MaxEnt RL can be obtained from the Perron-Frobenius eigenvalue and the corresponding left eigenvector of a regular, non-negative matrix derived from the underlying Markov Decision Process (MDP). The results derived lead to novel algorithms for model-based and model-free MaxEnt RL, which we validate by numerical simulations. The mapping established in this work opens further avenues for the application of novel analytical and computational approaches to problems in MaxEnt RL. We make our code available at: https://github.com/argearriojas/maxent-rl-mdp-scripts