Wooyoung Chung
Dimensionality Reduction of Dynamics on Lie Manifolds via Structure-Aware Canonical Correlation Analysis
Nov 17, 2023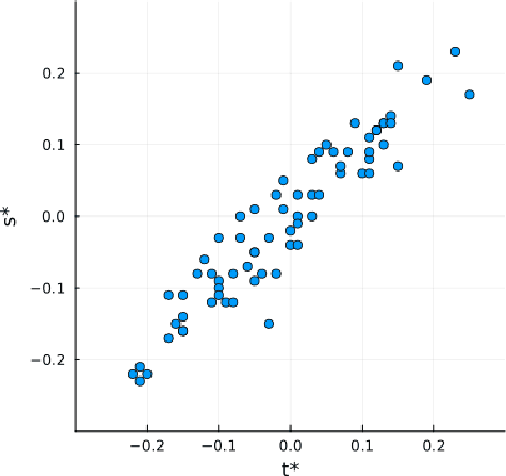
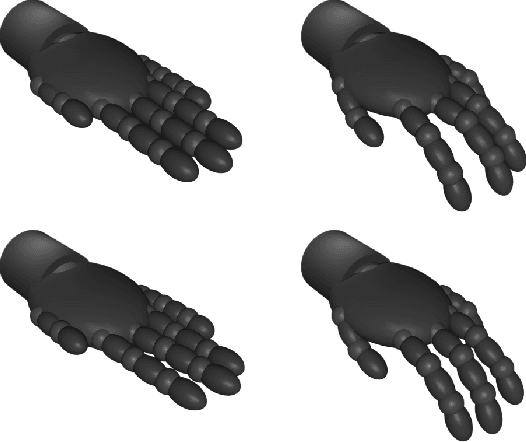
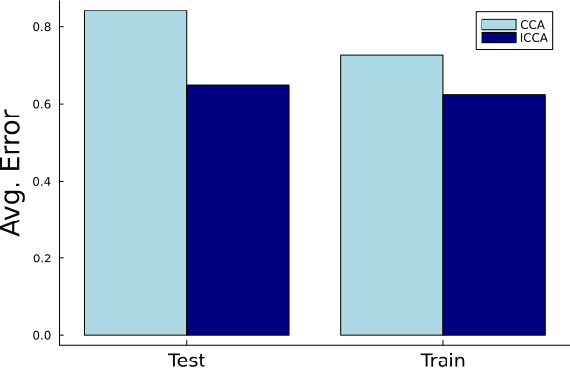
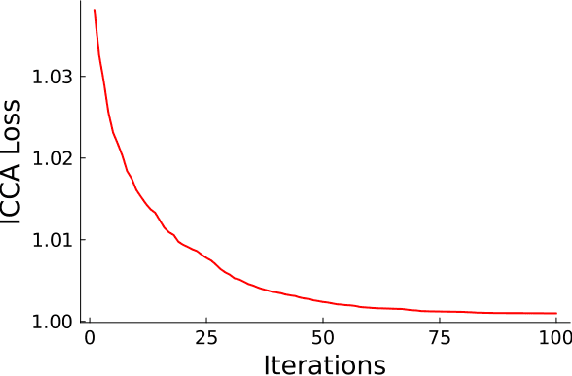
Abstract:Incorporating prior knowledge into a data-driven modeling problem can drastically improve performance, reliability, and generalization outside of the training sample. The stronger the structural properties, the more effective these improvements become. Manifolds are a powerful nonlinear generalization of Euclidean space for modeling finite dimensions. Structural impositions in constrained systems increase when applying group structure, converting them into Lie manifolds. The range of their applications is very wide and includes the important case of robotic tasks. Canonical Correlation Analysis (CCA) can construct a hierarchical sequence of maximal correlations of up to two paired data sets in these Euclidean spaces. We present a method to generalize this concept to Lie Manifolds and demonstrate its efficacy through the substantial improvements it achieves in making structure-consistent predictions about changes in the state of a robotic hand.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge