Deep Variational Multivariate Information Bottleneck -- A Framework for Variational Losses

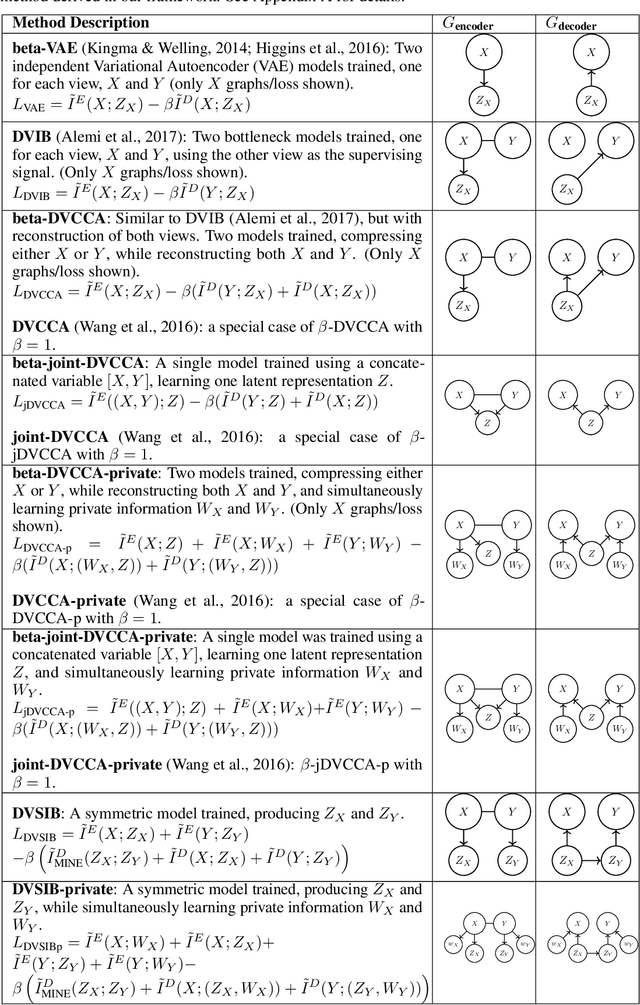
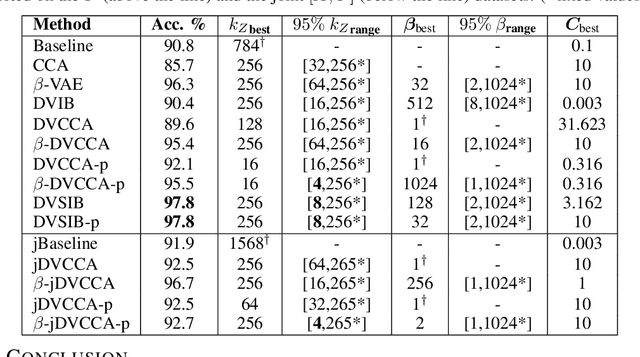
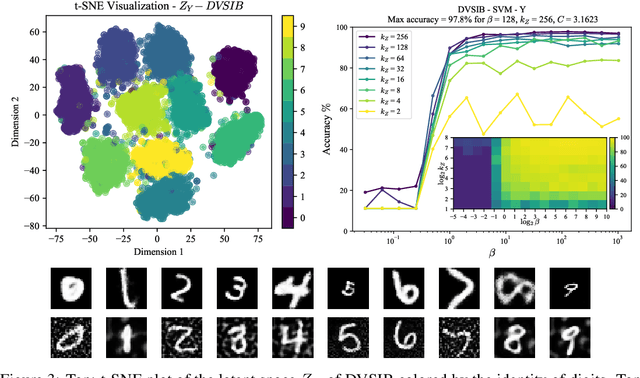
Variational dimensionality reduction methods are known for their high accuracy, generative abilities, and robustness. These methods have many theoretical justifications. Here we introduce a unifying principle rooted in information theory to rederive and generalize existing variational methods and design new ones. We base our framework on an interpretation of the multivariate information bottleneck, in which two Bayesian networks are traded off against one another. We interpret the first network as an encoder graph, which specifies what information to keep when compressing the data. We interpret the second network as a decoder graph, which specifies a generative model for the data. Using this framework, we rederive existing dimensionality reduction methods such as the deep variational information bottleneck (DVIB), beta variational auto-encoders (beta-VAE), and deep variational canonical correlation analysis (DVCCA). The framework naturally introduces a trade-off parameter between compression and reconstruction in the DVCCA family of algorithms, resulting in the new beta-DVCCA family. In addition, we derive a new variational dimensionality reduction method, deep variational symmetric informational bottleneck (DVSIB), which simultaneously compresses two variables to preserve information between their compressed representations. We implement all of these algorithms and evaluate their ability to produce shared low dimensional latent spaces on a modified noisy MNIST dataset. We show that algorithms that are better matched to the structure of the data (beta-DVCCA and DVSIB) produce better latent spaces as measured by classification accuracy and the dimensionality of the latent variables. We believe that this framework can be used to unify other multi-view representation learning algorithms. Additionally, it provides a straightforward framework for deriving problem-specific loss functions.