Simultaneous Dimensionality Reduction: A Data Efficient Approach for Multimodal Representations Learning

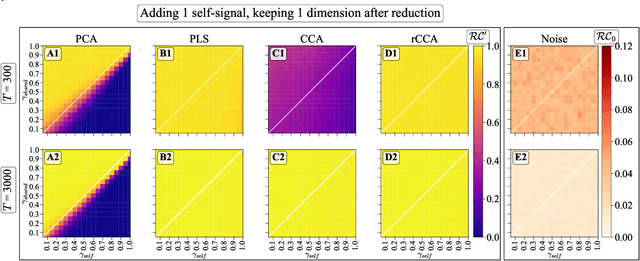
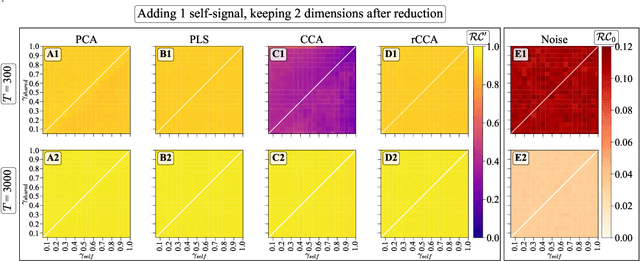
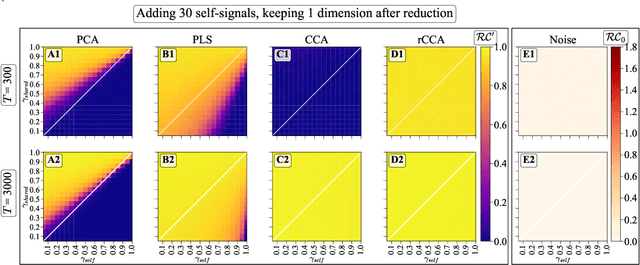
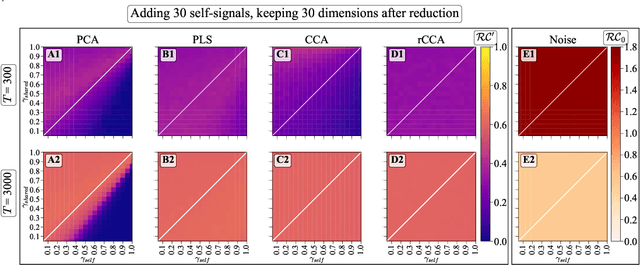
We explore two primary classes of approaches to dimensionality reduction (DR): Independent Dimensionality Reduction (IDR) and Simultaneous Dimensionality Reduction (SDR). In IDR methods, of which Principal Components Analysis is a paradigmatic example, each modality is compressed independently, striving to retain as much variation within each modality as possible. In contrast, in SDR, one simultaneously compresses the modalities to maximize the covariation between the reduced descriptions while paying less attention to how much individual variation is preserved. Paradigmatic examples include Partial Least Squares and Canonical Correlations Analysis. Even though these DR methods are a staple of statistics, their relative accuracy and data set size requirements are poorly understood. We introduce a generative linear model to synthesize multimodal data with known variance and covariance structures to examine these questions. We assess the accuracy of the reconstruction of the covariance structures as a function of the number of samples, signal-to-noise ratio, and the number of varying and covarying signals in the data. Using numerical experiments, we demonstrate that linear SDR methods consistently outperform linear IDR methods and yield higher-quality, more succinct reduced-dimensional representations with smaller datasets. Remarkably, regularized CCA can identify low-dimensional weak covarying structures even when the number of samples is much smaller than the dimensionality of the data, which is a regime challenging for all dimensionality reduction methods. Our work corroborates and explains previous observations in the literature that SDR can be more effective in detecting covariation patterns in data. These findings suggest that SDR should be preferred to IDR in real-world data analysis when detecting covariation is more important than preserving variation.

Deep Variational Multivariate Information Bottleneck -- A Framework for Variational Losses

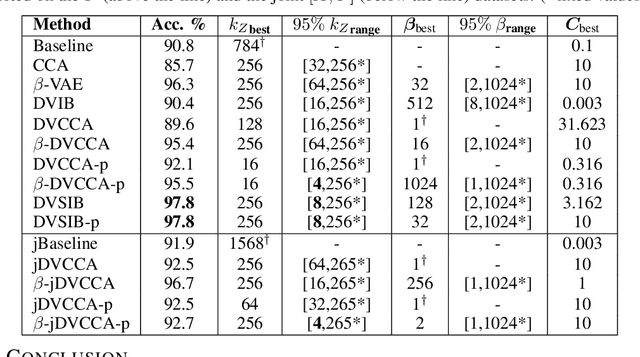
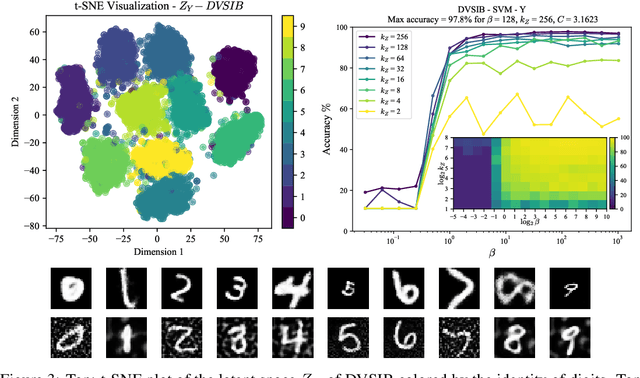
Variational dimensionality reduction methods are known for their high accuracy, generative abilities, and robustness. These methods have many theoretical justifications. Here we introduce a unifying principle rooted in information theory to rederive and generalize existing variational methods and design new ones. We base our framework on an interpretation of the multivariate information bottleneck, in which two Bayesian networks are traded off against one another. We interpret the first network as an encoder graph, which specifies what information to keep when compressing the data. We interpret the second network as a decoder graph, which specifies a generative model for the data. Using this framework, we rederive existing dimensionality reduction methods such as the deep variational information bottleneck (DVIB), beta variational auto-encoders (beta-VAE), and deep variational canonical correlation analysis (DVCCA). The framework naturally introduces a trade-off parameter between compression and reconstruction in the DVCCA family of algorithms, resulting in the new beta-DVCCA family. In addition, we derive a new variational dimensionality reduction method, deep variational symmetric informational bottleneck (DVSIB), which simultaneously compresses two variables to preserve information between their compressed representations. We implement all of these algorithms and evaluate their ability to produce shared low dimensional latent spaces on a modified noisy MNIST dataset. We show that algorithms that are better matched to the structure of the data (beta-DVCCA and DVSIB) produce better latent spaces as measured by classification accuracy and the dimensionality of the latent variables. We believe that this framework can be used to unify other multi-view representation learning algorithms. Additionally, it provides a straightforward framework for deriving problem-specific loss functions.

Data efficiency, dimensionality reduction, and the generalized symmetric information bottleneck

The Symmetric Information Bottleneck (SIB), an extension of the more familiar Information Bottleneck, is a dimensionality reduction technique that simultaneously compresses two random variables to preserve information between their compressed versions. We introduce the Generalized Symmetric Information Bottleneck (GSIB), which explores different functional forms of the cost of such simultaneous reduction. We then explore the dataset size requirements of such simultaneous compression. We do this by deriving bounds and root-mean-squared estimates of statistical fluctuations of the involved loss functions. We show that, in typical situations, the simultaneous GSIB compression requires qualitatively less data to achieve the same errors compared to compressing variables one at a time. We suggest that this is an example of a more general principle that simultaneous compression is more data efficient than independent compression of each of the input variables.