Simultaneous Dimensionality Reduction: A Data Efficient Approach for Multimodal Representations Learning
Paper and Code
Oct 05, 2023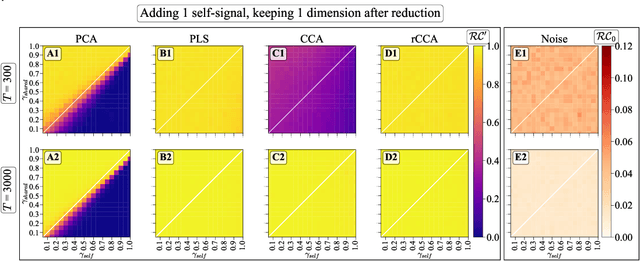
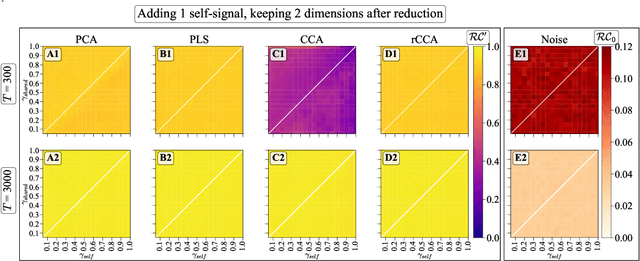
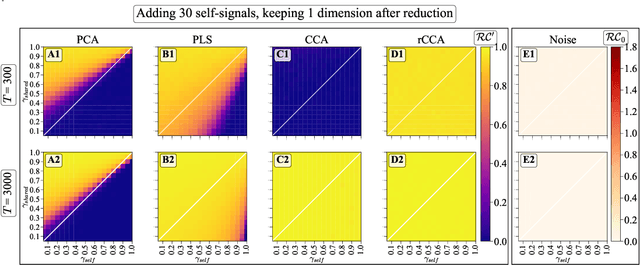
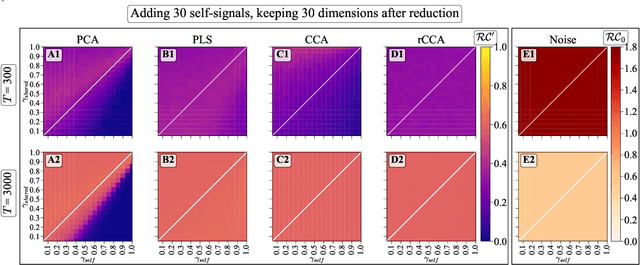
We explore two primary classes of approaches to dimensionality reduction (DR): Independent Dimensionality Reduction (IDR) and Simultaneous Dimensionality Reduction (SDR). In IDR methods, of which Principal Components Analysis is a paradigmatic example, each modality is compressed independently, striving to retain as much variation within each modality as possible. In contrast, in SDR, one simultaneously compresses the modalities to maximize the covariation between the reduced descriptions while paying less attention to how much individual variation is preserved. Paradigmatic examples include Partial Least Squares and Canonical Correlations Analysis. Even though these DR methods are a staple of statistics, their relative accuracy and data set size requirements are poorly understood. We introduce a generative linear model to synthesize multimodal data with known variance and covariance structures to examine these questions. We assess the accuracy of the reconstruction of the covariance structures as a function of the number of samples, signal-to-noise ratio, and the number of varying and covarying signals in the data. Using numerical experiments, we demonstrate that linear SDR methods consistently outperform linear IDR methods and yield higher-quality, more succinct reduced-dimensional representations with smaller datasets. Remarkably, regularized CCA can identify low-dimensional weak covarying structures even when the number of samples is much smaller than the dimensionality of the data, which is a regime challenging for all dimensionality reduction methods. Our work corroborates and explains previous observations in the literature that SDR can be more effective in detecting covariation patterns in data. These findings suggest that SDR should be preferred to IDR in real-world data analysis when detecting covariation is more important than preserving variation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge