The Dual Information Bottleneck
Paper and Code
Jun 08, 2020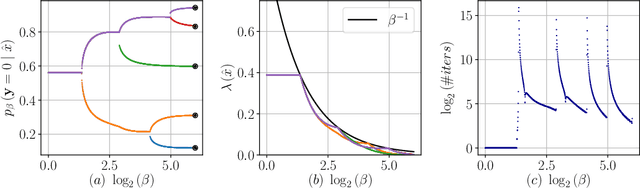
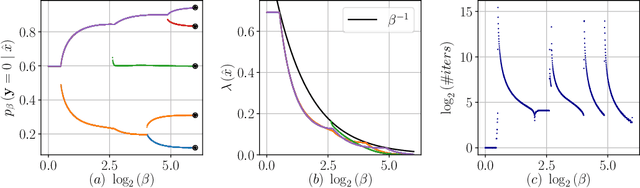
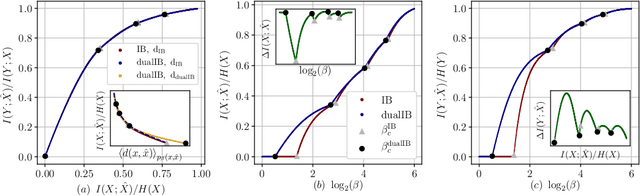

The Information Bottleneck (IB) framework is a general characterization of optimal representations obtained using a principled approach for balancing accuracy and complexity. Here we present a new framework, the Dual Information Bottleneck (dualIB), which resolves some of the known drawbacks of the IB. We provide a theoretical analysis of the dualIB framework; (i) solving for the structure of its solutions (ii) unraveling its superiority in optimizing the mean prediction error exponent and (iii) demonstrating its ability to preserve exponential forms of the original distribution. To approach large scale problems, we present a novel variational formulation of the dualIB for Deep Neural Networks. In experiments on several data-sets, we compare it to a variational form of the IB. This exposes superior Information Plane properties of the dualIB and its potential in improvement of the error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge