Irit Levin Reisman
Detecting chaos in lineage-trees: A deep learning approach
Jun 08, 2021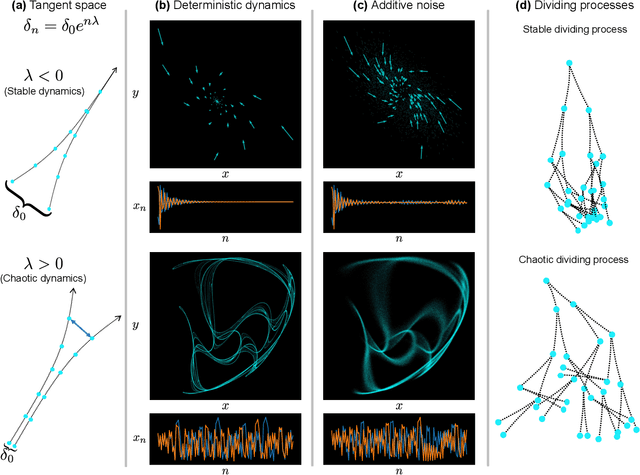
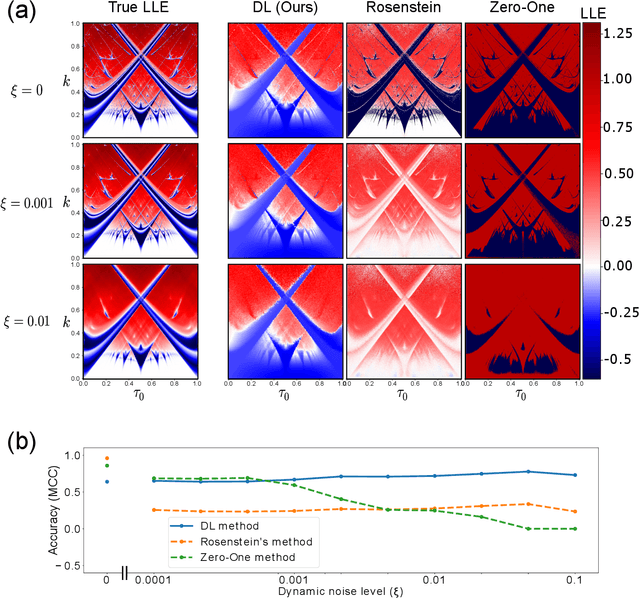
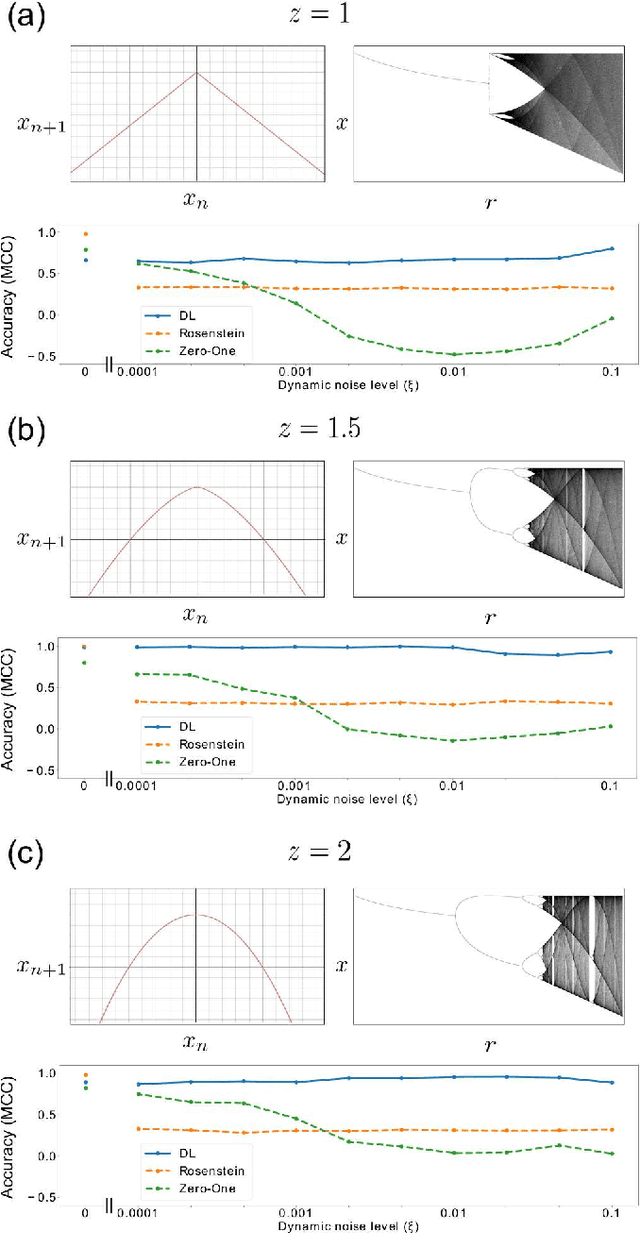
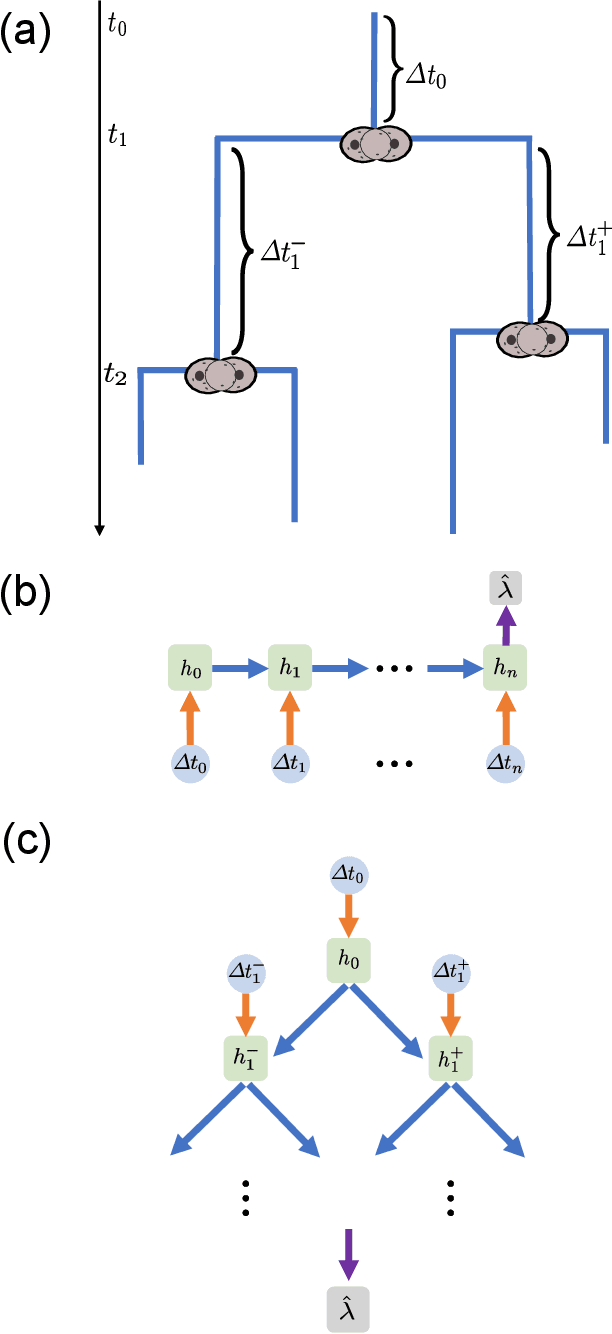
Abstract:Many complex phenomena, from weather systems to heartbeat rhythm patterns, are effectively modeled as low-dimensional dynamical systems. Such systems may behave chaotically under certain conditions, and so the ability to detect chaos based on empirical measurement is an important step in characterizing and predicting these processes. Classifying a system as chaotic usually requires estimating its largest Lyapunov exponent, which quantifies the average rate of convergence or divergence of initially close trajectories in state space, and for which a positive value is generally accepted as an operational definition of chaos. Estimating the largest Lyapunov exponent from observations of a process is especially challenging in systems affected by dynamical noise, which is the case for many models of real-world processes, in particular models of biological systems. We describe a novel method for estimating the largest Lyapunov exponent from data, based on training Deep Learning models on synthetically generated trajectories, and demonstrate that this method yields accurate and noise-robust predictions given relatively short inputs and across a range of different dynamical systems. Our method is unique in that it can analyze tree-shaped data, a ubiquitous topology in biological settings, and specifically in dynamics over lineages of cells or organisms. We also characterize the types of input information extracted by our models for their predictions, allowing for a deeper understanding into the different ways by which chaos can be analyzed in different topologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge