Tensor-Based Synchronization and the Low-Rankness of the Block Trifocal Tensor

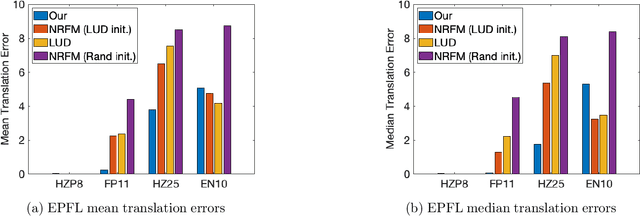
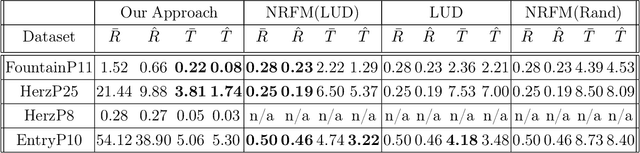
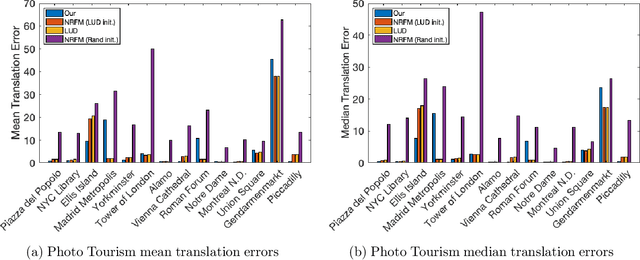
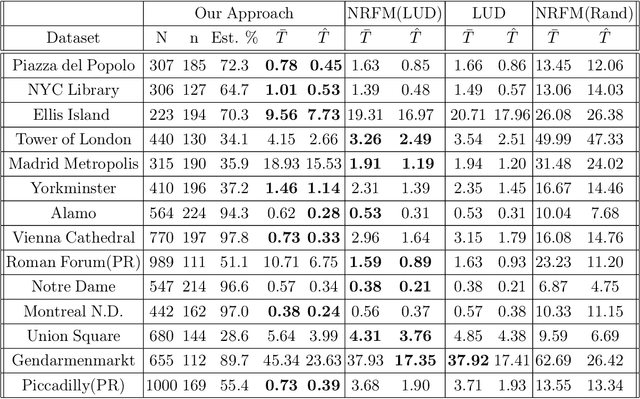
The block tensor of trifocal tensors provides crucial geometric information on the three-view geometry of a scene. The underlying synchronization problem seeks to recover camera poses (locations and orientations up to a global transformation) from the block trifocal tensor. We establish an explicit Tucker factorization of this tensor, revealing a low multilinear rank of $(6,4,4)$ independent of the number of cameras under appropriate scaling conditions. We prove that this rank constraint provides sufficient information for camera recovery in the noiseless case. The constraint motivates a synchronization algorithm based on the higher-order singular value decomposition of the block trifocal tensor. Experimental comparisons with state-of-the-art global synchronization methods on real datasets demonstrate the potential of this algorithm for significantly improving location estimation accuracy. Overall this work suggests that higher-order interactions in synchronization problems can be exploited to improve performance, beyond the usual pairwise-based approaches.

Moment-based metrics for molecules computable from cryo-EM images

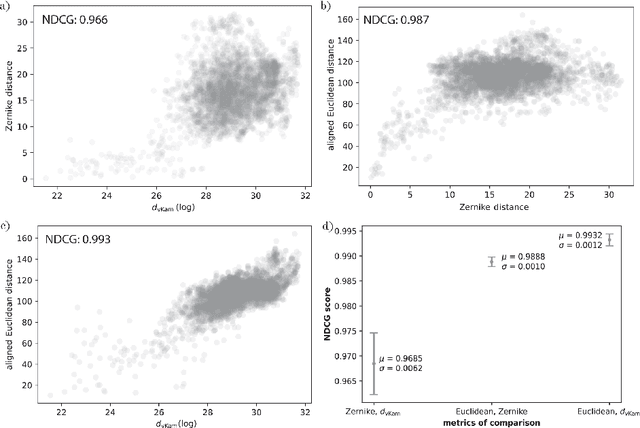
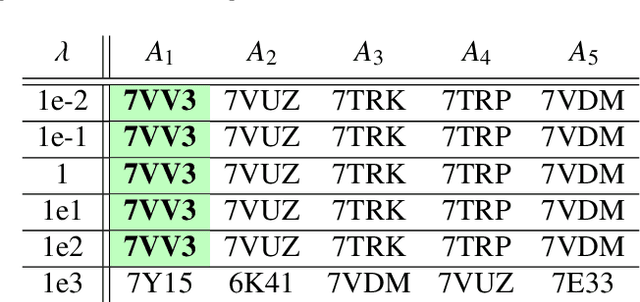
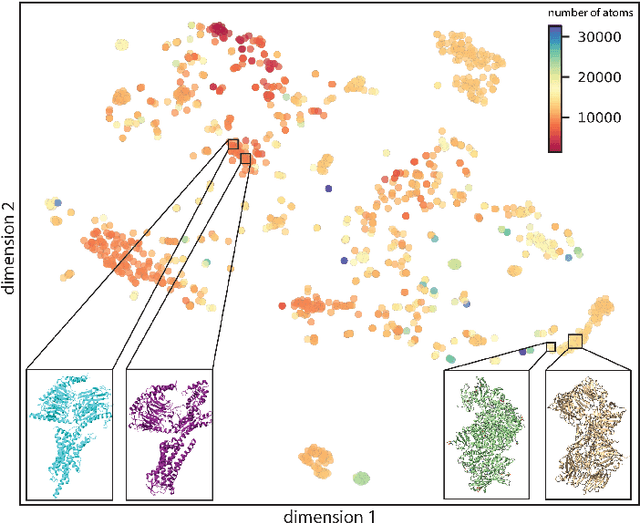
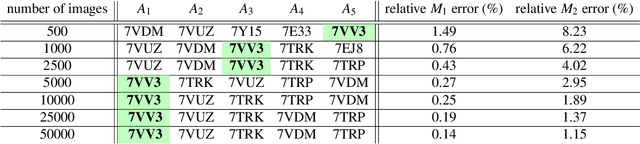
Single particle cryogenic electron microscopy (cryo-EM) is an imaging technique capable of recovering the high-resolution 3-D structure of biological macromolecules from many noisy and randomly oriented projection images. One notable approach to 3-D reconstruction, known as Kam's method, relies on the moments of the 2-D images. Inspired by Kam's method, we introduce a rotationally invariant metric between two molecular structures, which does not require 3-D alignment. Further, we introduce a metric between a stack of projection images and a molecular structure, which is invariant to rotations and reflections and does not require performing 3-D reconstruction. Additionally, the latter metric does not assume a uniform distribution of viewing angles. We demonstrate uses of the new metrics on synthetic and experimental datasets, highlighting their ability to measure structural similarity.

Covering Number of Real Algebraic Varieties and Beyond: Improved Bounds and Applications

We prove an upper bound on the covering number of real algebraic varieties, images of polynomial maps and semialgebraic sets. The bound remarkably improves the best known general bound by Yomdin-Comte, and its proof is much more straightforward. As a consequence, our result gives new bounds on the volume of the tubular neighborhood of the image of a polynomial map and a semialgebraic set, where results for varieties by Lotz and Basu-Lerario are not directly applicable. We apply our theory to three main application domains. Firstly, we derive a near-optimal bound on the covering number of low rank CP tensors. Secondly, we prove a bound on the sketching dimension for (general) polynomial optimization problems. Lastly, we deduce generalization error bounds for deep neural networks with rational or ReLU activations, improving or matching the best known results in the literature.

Condition numbers in multiview geometry, instability in relative pose estimation, and RANSAC

In this paper we introduce a general framework for analyzing the numerical conditioning of minimal problems in multiple view geometry, using tools from computational algebra and Riemannian geometry. Special motivation comes from the fact that relative pose estimation, based on standard 5-point or 7-point Random Sample Consensus (RANSAC) algorithms, can fail even when no outliers are present and there is enough data to support a hypothesis. We argue that these cases arise due to the intrinsic instability of the 5- and 7-point minimal problems. We apply our framework to characterize the instabilities, both in terms of the world scenes that lead to infinite condition number, and directly in terms of ill-conditioned image data. The approach produces computational tests for assessing the condition number before solving the minimal problem. Lastly synthetic and real data experiments suggest that RANSAC serves not only to remove outliers, but also to select for well-conditioned image data, as predicted by our theory.

Diffusion Maps for Group-Invariant Manifolds

In this article, we consider the manifold learning problem when the data set is invariant under the action of a compact Lie group $K$. Our approach consists in augmenting the data-induced graph Laplacian by integrating over the $K$-orbits of the existing data points, which yields a $K$-invariant graph Laplacian $L$. We prove that $L$ can be diagonalized by using the unitary irreducible representation matrices of $K$, and we provide an explicit formula for computing its eigenvalues and eigenfunctions. In addition, we show that the normalized Laplacian operator $L_N$ converges to the Laplace-Beltrami operator of the data manifold with an improved convergence rate, where the improvement grows with the dimension of the symmetry group $K$. This work extends the steerable graph Laplacian framework of Landa and Shkolnisky from the case of $\operatorname{SO}(2)$ to arbitrary compact Lie groups.

Moment Estimation for Nonparametric Mixture Models Through Implicit Tensor Decomposition

We present an alternating least squares type numerical optimization scheme to estimate conditionally-independent mixture models in $\mathbb{R}^n$, with minimal additional distributional assumptions. Following the method of moments, we tackle a coupled system of low-rank tensor decomposition problems. The steep costs associated with high-dimensional tensors are avoided, through the development of specialized tensor-free operations. Numerical experiments illustrate the performance of the algorithm and its applicability to various models and applications. In many cases the results exhibit improved reliability over the expectation-maximization algorithm, with similar time and storage costs. We also provide some supporting theory, establishing identifiability and local linear convergence.

Snapshot of Algebraic Vision

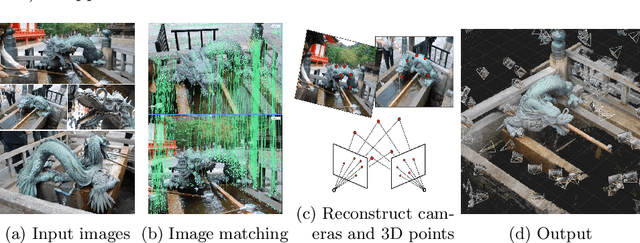
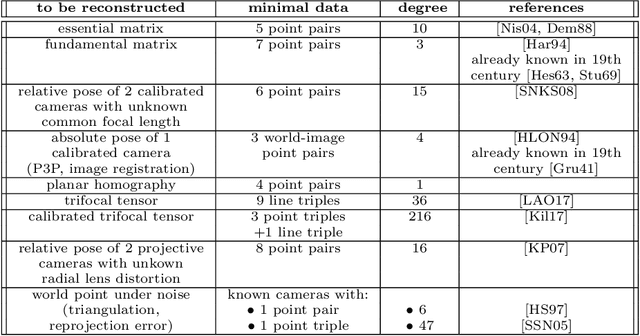
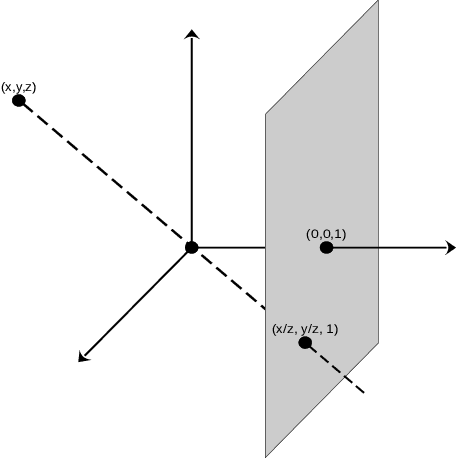
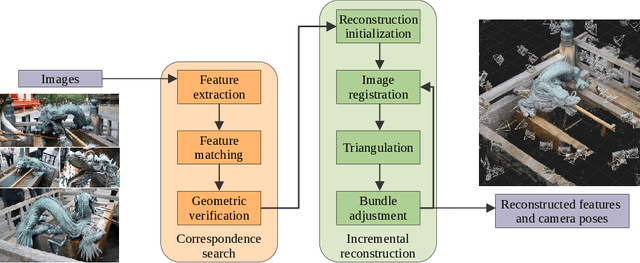
In this survey article, we present interactions between algebraic geometry and computer vision, which have recently come under the header of Algebraic Vision. The subject has given new insights in multiple view geometry and its application to 3D scene reconstruction, and carried a host of novel problems and ideas back into algebraic geometry.

Tensor Moments of Gaussian Mixture Models: Theory and Applications

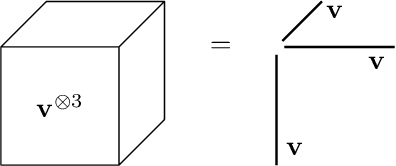
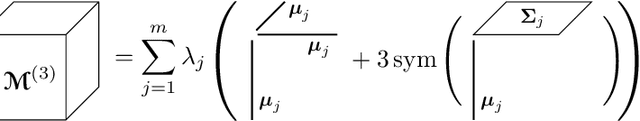
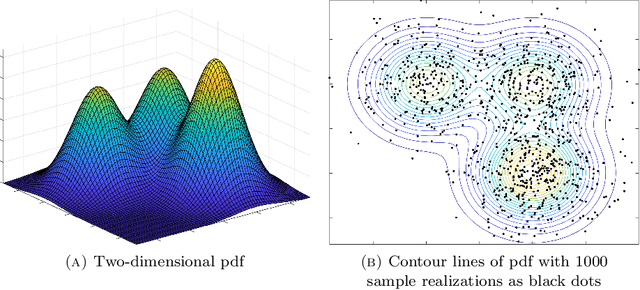
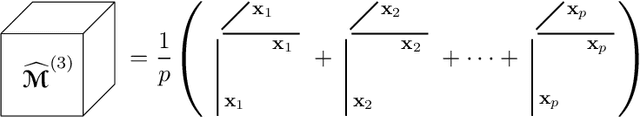
Gaussian mixture models (GMM) are fundamental tools in statistical and data sciences. We study the moments of multivariate Gaussians and GMMs. The $d$-th moment of an $n$-dimensional random variable is a symmetric $d$-way tensor of size $n^d$, so working with moments naively is assumed to be prohibitively expensive for $d>2$ and larger values of $n$. In this work, we develop theory and numerical methods for implicit computations with moment tensors of GMMs, reducing the computational and storage costs to $\mathcal{O}(n^2)$ and $\mathcal{O}(n^3)$, respectively, for general covariance matrices, and to $\mathcal{O}(n)$ and $\mathcal{O}(n)$, respectively, for diagonal ones. We derive concise analytic expressions for the moments in terms of symmetrized tensor products, relying on the correspondence between symmetric tensors and homogeneous polynomials, and combinatorial identities involving Bell polynomials. The primary application of this theory is to estimating GMM parameters from a set of observations, when formulated as a moment-matching optimization problem. If there is a known and common covariance matrix, we also show it is possible to debias the data observations, in which case the problem of estimating the unknown means reduces to symmetric CP tensor decomposition. Numerical results validate and illustrate the numerical efficiency of our approaches. This work potentially opens the door to the competitiveness of the method of moments as compared to expectation maximization methods for parameter estimation of GMMs.

On the Instability of Relative Pose Estimation and RANSAC's Role

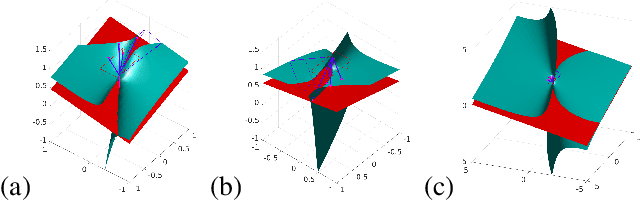
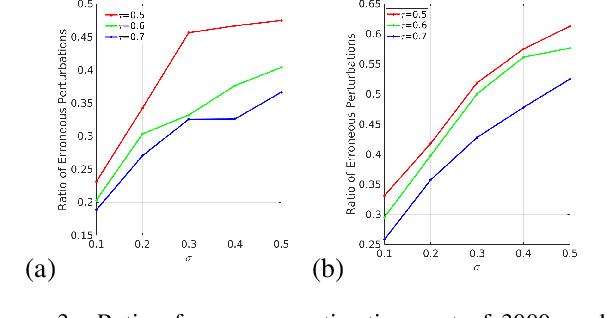
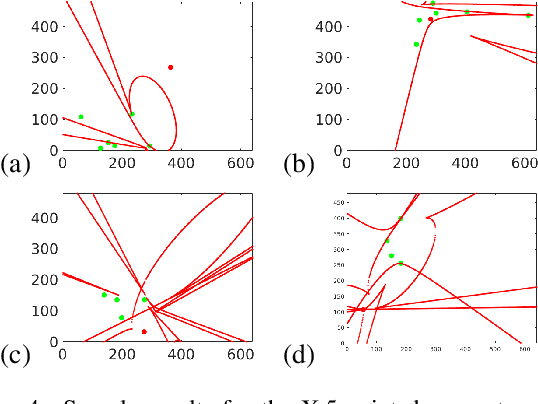
In this paper we study the numerical instabilities of the 5- and 7-point problems for essential and fundamental matrix estimation in multiview geometry. In both cases we characterize the ill-posed world scenes where the condition number for epipolar estimation is infinite. We also characterize the ill-posed instances in terms of the given image data. To arrive at these results, we present a general framework for analyzing the conditioning of minimal problems in multiview geometry, based on Riemannian manifolds. Experiments with synthetic and real-world data then reveal a striking conclusion: that Random Sample Consensus (RANSAC) in Structure-from-Motion (SfM) does not only serve to filter out outliers, but RANSAC also selects for well-conditioned image data, sufficiently separated from the ill-posed locus that our theory predicts. Our findings suggest that, in future work, one could try to accelerate and increase the success of RANSAC by testing only well-conditioned image data.

Landscape analysis of an improved power method for tensor decomposition

In this work, we consider the optimization formulation for symmetric tensor decomposition recently introduced in the Subspace Power Method (SPM) of Kileel and Pereira. Unlike popular alternative functionals for tensor decomposition, the SPM objective function has the desirable properties that its maximal value is known in advance, and its global optima are exactly the rank-1 components of the tensor when the input is sufficiently low-rank. We analyze the non-convex optimization landscape associated with the SPM objective. Our analysis accounts for working with noisy tensors. We derive quantitative bounds such that any second-order critical point with SPM objective value exceeding the bound must equal a tensor component in the noiseless case, and must approximate a tensor component in the noisy case. For decomposing tensors of size $D^{\times m}$, we obtain a near-global guarantee up to rank $\widetilde{o}(D^{\lfloor m/2 \rfloor})$ under a random tensor model, and a global guarantee up to rank $\mathcal{O}(D)$ assuming deterministic frame conditions. This implies that SPM with suitable initialization is a provable, efficient, robust algorithm for low-rank symmetric tensor decomposition. We conclude with numerics that show a practical preferability for using the SPM functional over a more established counterpart.