Gilad Lerman
Learning to Charge More: A Theoretical Study of Collusion by Q-Learning Agents
May 28, 2025Abstract:There is growing experimental evidence that $Q$-learning agents may learn to charge supracompetitive prices. We provide the first theoretical explanation for this behavior in infinite repeated games. Firms update their pricing policies based solely on observed profits, without computing equilibrium strategies. We show that when the game admits both a one-stage Nash equilibrium price and a collusive-enabling price, and when the $Q$-function satisfies certain inequalities at the end of experimentation, firms learn to consistently charge supracompetitive prices. We introduce a new class of one-memory subgame perfect equilibria (SPEs) and provide conditions under which learned behavior is supported by naive collusion, grim trigger policies, or increasing strategies. Naive collusion does not constitute an SPE unless the collusive-enabling price is a one-stage Nash equilibrium, whereas grim trigger policies can.
Stein Discrepancy for Unsupervised Domain Adaptation
Feb 05, 2025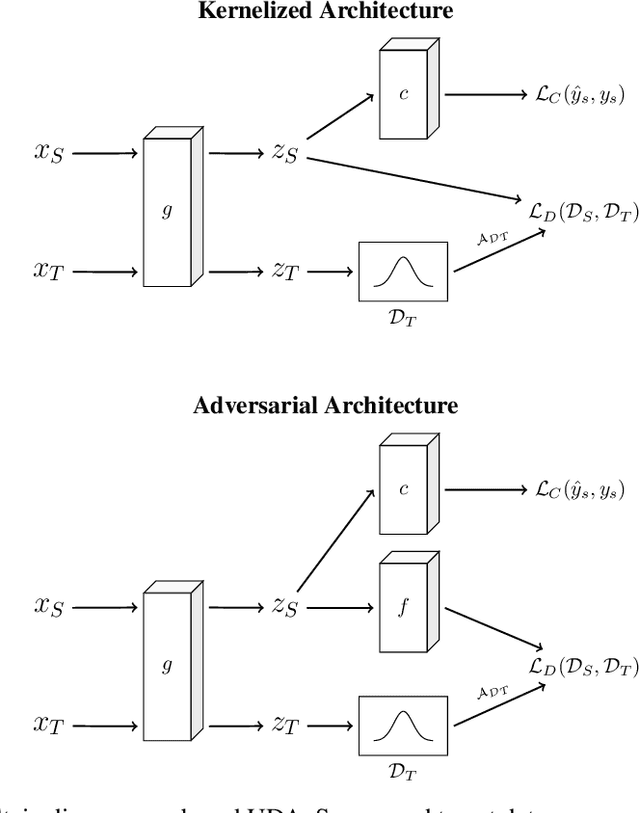
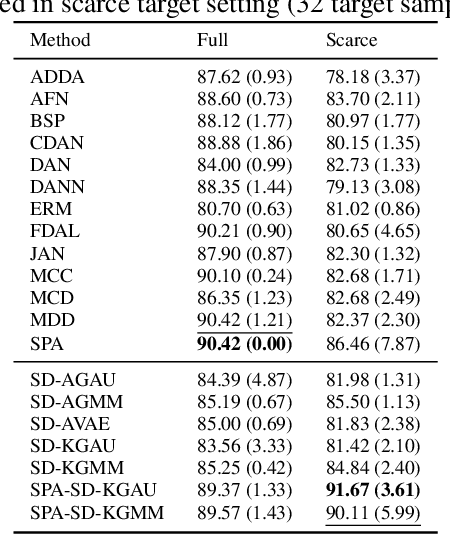
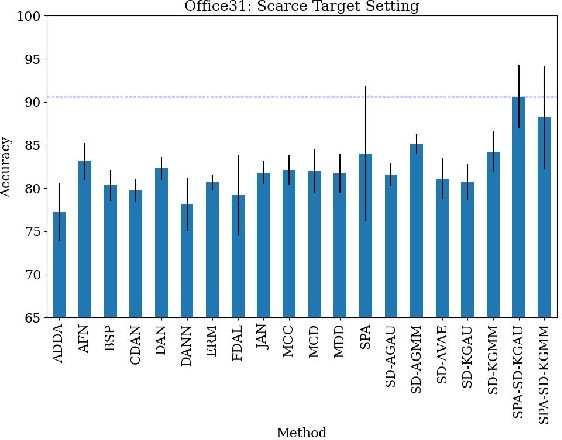
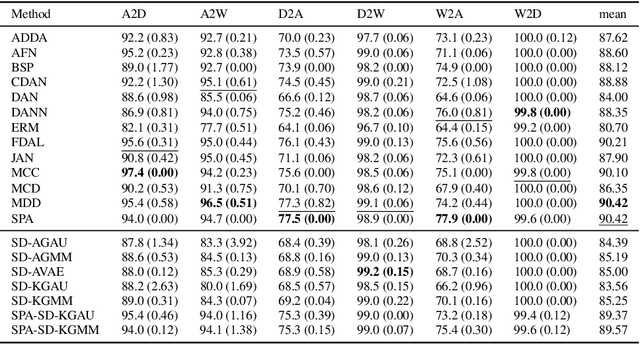
Abstract:Unsupervised domain adaptation (UDA) leverages information from a labeled source dataset to improve accuracy on a related but unlabeled target dataset. A common approach to UDA is aligning representations from the source and target domains by minimizing the distance between their data distributions. Previous methods have employed distances such as Wasserstein distance and maximum mean discrepancy. However, these approaches are less effective when the target data is significantly scarcer than the source data. Stein discrepancy is an asymmetric distance between distributions that relies on one distribution only through its score function. In this paper, we propose a novel \ac{uda} method that uses Stein discrepancy to measure the distance between source and target domains. We develop a learning framework using both non-kernelized and kernelized Stein discrepancy. Theoretically, we derive an upper bound for the generalization error. Numerical experiments show that our method outperforms existing methods using other domain discrepancy measures when only small amounts of target data are available.
Tensor-Based Synchronization and the Low-Rankness of the Block Trifocal Tensor
Sep 14, 2024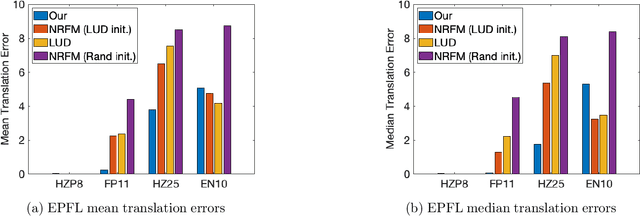
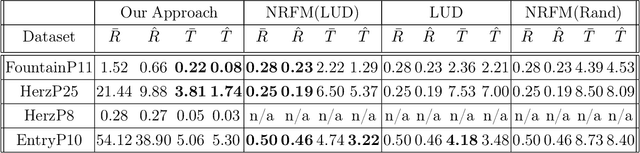
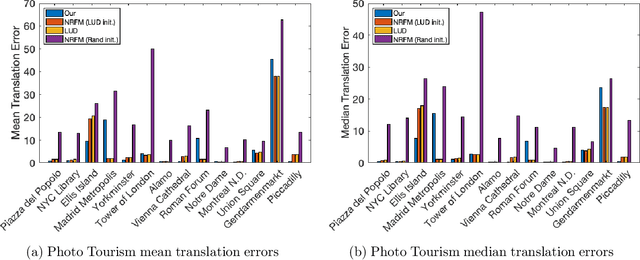
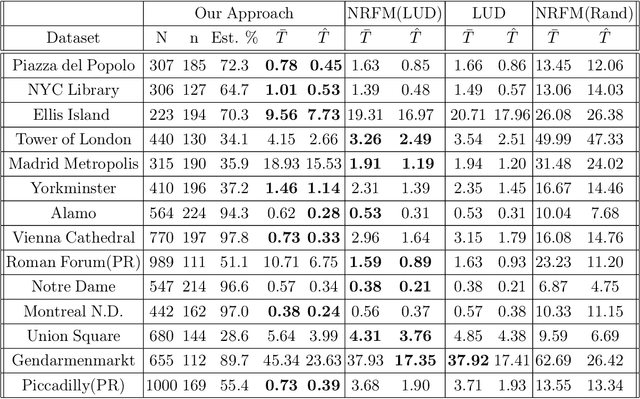
Abstract:The block tensor of trifocal tensors provides crucial geometric information on the three-view geometry of a scene. The underlying synchronization problem seeks to recover camera poses (locations and orientations up to a global transformation) from the block trifocal tensor. We establish an explicit Tucker factorization of this tensor, revealing a low multilinear rank of $(6,4,4)$ independent of the number of cameras under appropriate scaling conditions. We prove that this rank constraint provides sufficient information for camera recovery in the noiseless case. The constraint motivates a synchronization algorithm based on the higher-order singular value decomposition of the block trifocal tensor. Experimental comparisons with state-of-the-art global synchronization methods on real datasets demonstrate the potential of this algorithm for significantly improving location estimation accuracy. Overall this work suggests that higher-order interactions in synchronization problems can be exploited to improve performance, beyond the usual pairwise-based approaches.
Improving Hyperbolic Representations via Gromov-Wasserstein Regularization
Jul 15, 2024
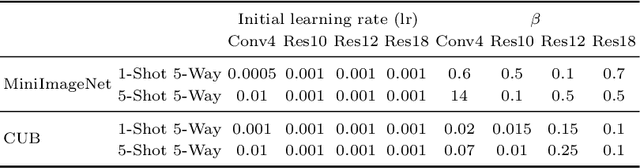
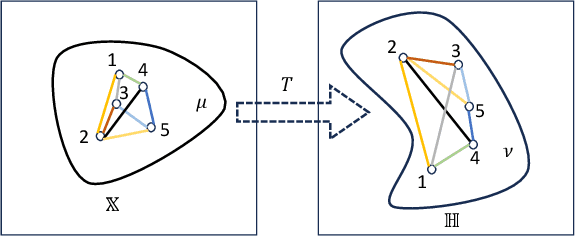
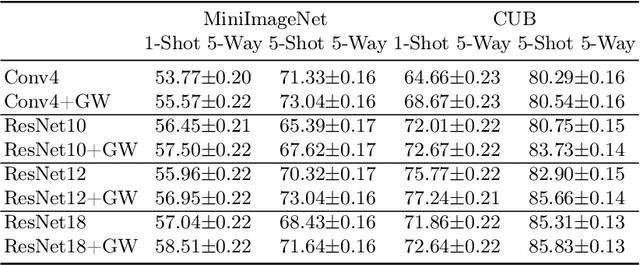
Abstract:Hyperbolic representations have shown remarkable efficacy in modeling inherent hierarchies and complexities within data structures. Hyperbolic neural networks have been commonly applied for learning such representations from data, but they often fall short in preserving the geometric structures of the original feature spaces. In response to this challenge, our work applies the Gromov-Wasserstein (GW) distance as a novel regularization mechanism within hyperbolic neural networks. The GW distance quantifies how well the original data structure is maintained after embedding the data in a hyperbolic space. Specifically, we explicitly treat the layers of the hyperbolic neural networks as a transport map and calculate the GW distance accordingly. We validate that the GW distance computed based on a training set well approximates the GW distance of the underlying data distribution. Our approach demonstrates consistent enhancements over current state-of-the-art methods across various tasks, including few-shot image classification, as well as semi-supervised graph link prediction and node classification.
Efficient Detection of Long Consistent Cycles and its Application to Distributed Synchronization
Jul 05, 2024
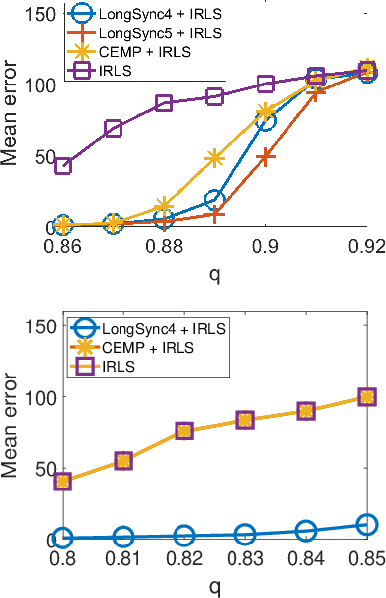

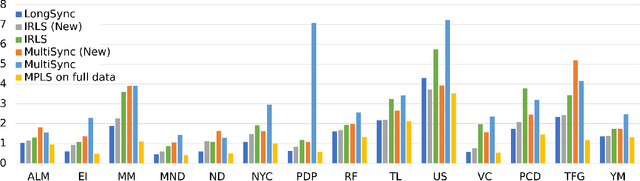
Abstract:Group synchronization plays a crucial role in global pipelines for Structure from Motion (SfM). Its formulation is nonconvex and it is faced with highly corrupted measurements. Cycle consistency has been effective in addressing these challenges. However, computationally efficient solutions are needed for cycles longer than three, especially in practical scenarios where 3-cycles are unavailable. To overcome this computational bottleneck, we propose an algorithm for group synchronization that leverages information from cycles of lengths ranging from three to six with a time complexity of order $O(n^3)$ (or $O(n^{2.373})$ when using a faster matrix multiplication algorithm). We establish non-trivial theory for this and related methods that achieves competitive sample complexity, assuming the uniform corruption model. To advocate the practical need for our method, we consider distributed group synchronization, which requires at least 4-cycles, and we illustrate state-of-the-art performance by our method in this context.
Artificial Intelligence and Algorithmic Price Collusion in Two-sided Markets
Jul 04, 2024



Abstract:Algorithmic price collusion facilitated by artificial intelligence (AI) algorithms raises significant concerns. We examine how AI agents using Q-learning engage in tacit collusion in two-sided markets. Our experiments reveal that AI-driven platforms achieve higher collusion levels compared to Bertrand competition. Increased network externalities significantly enhance collusion, suggesting AI algorithms exploit them to maximize profits. Higher user heterogeneity or greater utility from outside options generally reduce collusion, while higher discount rates increase it. Tacit collusion remains feasible even at low discount rates. To mitigate collusive behavior and inform potential regulatory measures, we propose incorporating a penalty term in the Q-learning algorithm.
A Subspace-Constrained Tyler's Estimator and its Applications to Structure from Motion
Apr 17, 2024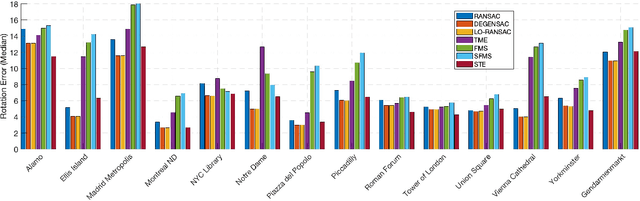
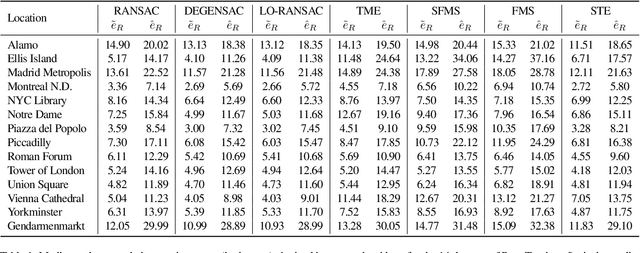
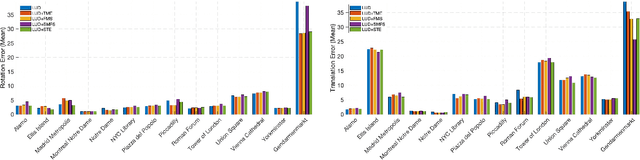
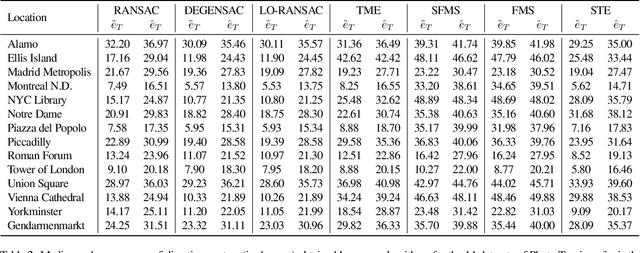
Abstract:We present the subspace-constrained Tyler's estimator (STE) designed for recovering a low-dimensional subspace within a dataset that may be highly corrupted with outliers. STE is a fusion of the Tyler's M-estimator (TME) and a variant of the fast median subspace. Our theoretical analysis suggests that, under a common inlier-outlier model, STE can effectively recover the underlying subspace, even when it contains a smaller fraction of inliers relative to other methods in the field of robust subspace recovery. We apply STE in the context of Structure from Motion (SfM) in two ways: for robust estimation of the fundamental matrix and for the removal of outlying cameras, enhancing the robustness of the SfM pipeline. Numerical experiments confirm the state-of-the-art performance of our method in these applications. This research makes significant contributions to the field of robust subspace recovery, particularly in the context of computer vision and 3D reconstruction.
Theoretical Guarantees for the Subspace-Constrained Tyler's Estimator
Mar 27, 2024Abstract:This work analyzes the subspace-constrained Tyler's estimator (STE) designed for recovering a low-dimensional subspace within a dataset that may be highly corrupted with outliers. It assumes a weak inlier-outlier model and allows the fraction of inliers to be smaller than a fraction that leads to computational hardness of the robust subspace recovery problem. It shows that in this setting, if the initialization of STE, which is an iterative algorithm, satisfies a certain condition, then STE can effectively recover the underlying subspace. It further shows that under the generalized haystack model, STE initialized by the Tyler's M-estimator (TME), can recover the subspace when the fraction of iniliers is too small for TME to handle.
The effect of Leaky ReLUs on the training and generalization of overparameterized networks
Feb 25, 2024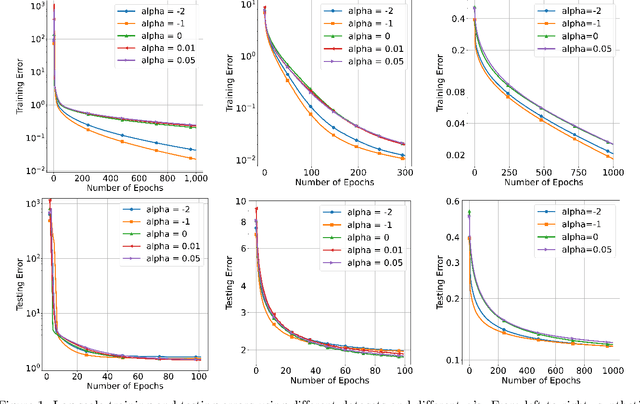


Abstract:We investigate the training and generalization errors of overparameterized neural networks (NNs) with a wide class of leaky rectified linear unit (ReLU) functions. More specifically, we carefully upper bound both the convergence rate of the training error and the generalization error of such NNs and investigate the dependence of these bounds on the Leaky ReLU parameter, $\alpha$. We show that $\alpha =-1$, which corresponds to the absolute value activation function, is optimal for the training error bound. Furthermore, in special settings, it is also optimal for the generalization error bound. Numerical experiments empirically support the practical choices guided by the theory.
Improved Convergence Rates of Anderson Acceleration for a Large Class of Fixed-Point Iterations
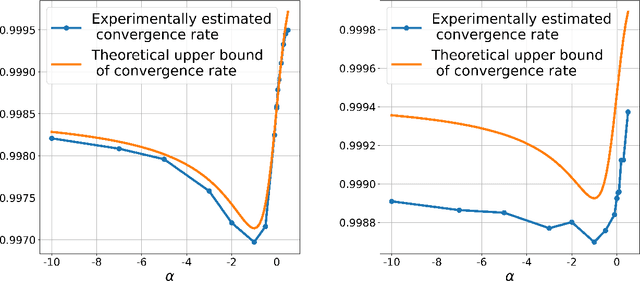
Nov 04, 2023Abstract:This paper studies Anderson acceleration (AA) for fixed-point methods ${x}^{(k+1)}=q({x}^{(k)})$. It provides the first proof that when the operator $q$ is linear and symmetric, AA improves the root-linear convergence factor over the fixed-point iterations. When $q$ is nonlinear, yet has a symmetric Jacobian at the solution, a slightly modified AA algorithm is proved to have an analogous root-linear convergence factor improvement over fixed-point iterations. Simulations verify our observations. Furthermore, experiments with different data models demonstrate AA is significantly superior to the standard fixed-point methods for Tyler's M-estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge